[精] 华师大版 数学七年级下册 课件 9多边形内角和与外角和

[精] 华师大版 数学七年级下册 课件 9多边形内角和与外角和

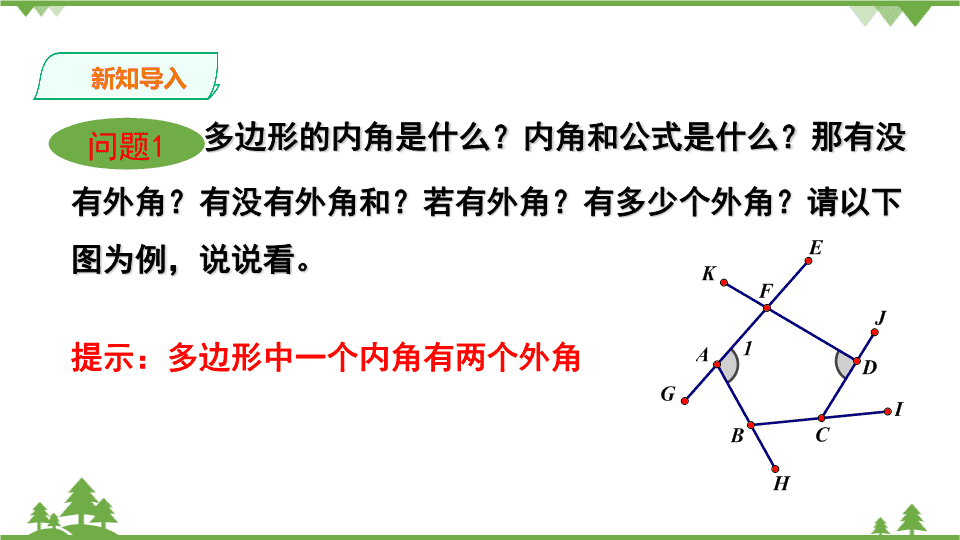
9.2多边形内角和与外角和第二课时第九章多边形 1.理解多边形外角的定义2.掌握多边形外角和3.灵活运用多边形内角和与外角和公式解决有关问题，体验并掌握探索、归纳图形性质的推理方法，进一步培养说理和进行简单推理的能力.。学习目标 多边形的内角是什么？内角和公式是什么？那有没有外角？有没有外角和？若有外角？有多少个外角？请以下图为例，说说看。问题1新知导入提示：多边形中一个内角有两个外角 新知导入想一想1、什么样的角时多边形的外角？2、怎样的角的和才算是多边形的外角和呢？多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。在每个顶点处取这个多边形的一个外角，他们的和叫做这个多边形的外角和。 问题2（1）小明从一条街道转到下一个街道时，身体转过的角是那个角？（2）他跑玩一圈，身体转过的角度之和是多少？（3）在右图中，你能求出∠1+∠2+∠3+∠4+∠5=？吗？你是怎么得到的？新知导入清晨，小明沿一个五边形的广场周围的小路，按逆时针方向跑步。 探究新知新知讲解12345αθβσγ结论：∠1+∠2+∠3+∠4+∠5=360° 新知讲解相信聪明的你好有其他办法证明这五个角的和。大家一起说一说！ 新知讲解我们可以借助多边形内角和来证明：∠1∠2∠3∠4∠5因为∠1+∠6=180°同理可得∠5+∠AED=180°∠4+∠EDC=180°∠3+∠BCD=180°∠2+∠ABC=180°则∠1+∠BAE+∠5+∠AED+∠4+∠EDC+∠3+∠BCD+∠2+∠ABC=5×180°又因为∠BAE+∠AED+∠EDC+∠BCD+∠ABC=540°所以∠1+∠2+∠3+∠4+∠5=360° 新知讲解那如果广场的形状是六边形、七边形、八边形…n边形呢？结论还是一样的么？分组合作多边形的边数多边形的外角和六边形七边形八边形...n边形 新知讲解任意多边形的外角和360° 新知讲解例3一个多边形的每个外角都是72°，这个多边形是几边形？解：设多边形的边数为n,根据题意，得n•72°=360°解得n=5因此这个多边形是五边形 新知讲解解：设多边形的边数为n.根据题意，得（n-2）•180°=5×360°解得n=12因此，这个多边形是十二边形例4一个多边形的内角和等于它外角和的5倍，这个多边形是几边形 课堂练习1、一个多边形的外角和是内角和的一半，则它是（）边形A7B6C5D42、一个多边形的内角和与外角和共540°，则它是（）边形A5B4C3D不确定BC 课堂练习3、若一个n边形的每一个内角都相等,且内角的度数与它相邻的外角的度数比为3:1，那么这个多边形的边数是。提示：可设n边形的内角为x°,则与它相邻的外角180°-x,根据题意可得x:180-x=3:1,解得x=135°则外角度数为45°这个多边形的边数为360°÷45°=8八边形 拓展提升利用多边形的内角和可以推出多边形的外角和，那如何利用多边形的外角和推出内角和的公式呢？ 课堂总结多边形的外角和定义多边形的外角和任意多边形外角和为360°通过本课时的学习，需要我们掌握 作业布置从教材中选择 谢谢