上海教育版数学第十三章《相交线 平行线》练习

上海教育版数学第十三章《相交线 平行线》练习

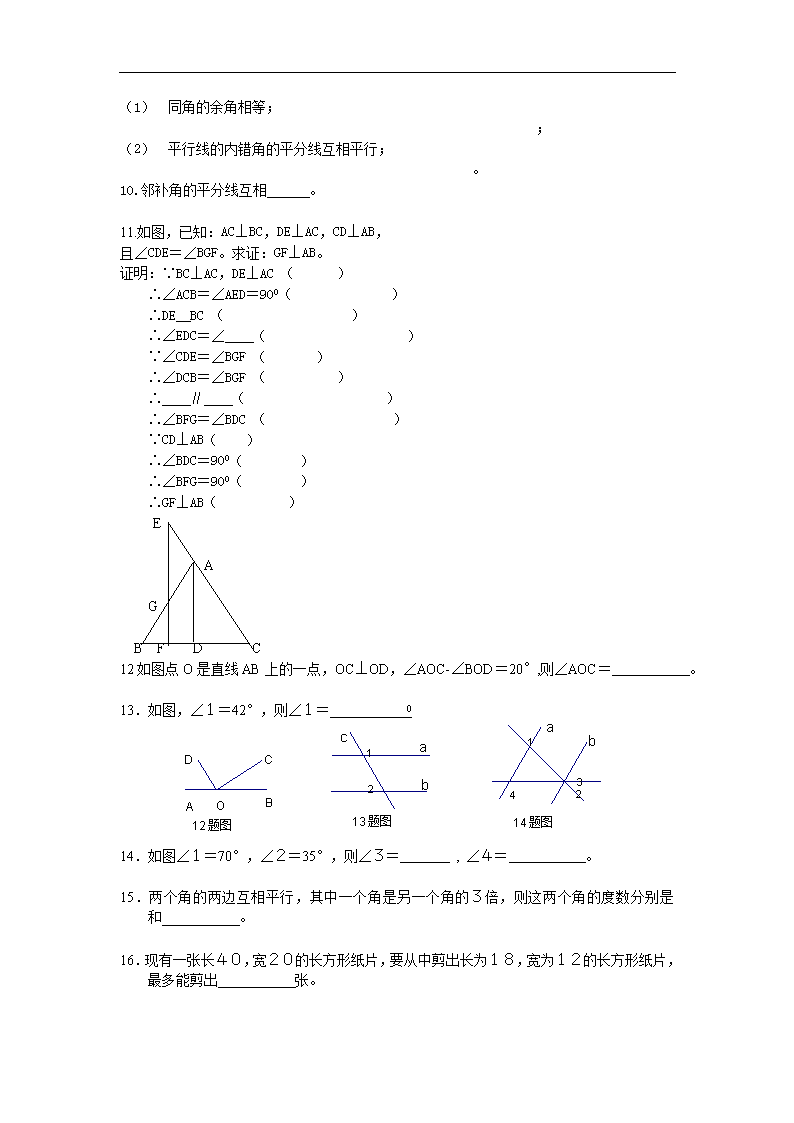
第十三章 相交线与平行线 知识梳理 1、相交直线：只有一个交点 邻补角 对顶角 斜交-----角平分线 垂直-----垂直的基本性质 -----点到直线的距离 -----线段的垂直平分线 两条直线被第三条直线所截-----同位角 -----内错角 -----同旁内角 2、平行直线：没有交点 平行线的性质定理 平行线的判定定理 ①平行线：在同一平面内，__________的两条直线叫做平行线。 ②在同一平面内，两条直线的位置关系只有两种：__________。相交时，对顶角相等。 ③平行线的判定： （1）同位角__________，两直线平行。 （2）内错角相等，两直线__________。 （3）同旁内角__________，两直线平行。 （4）平行（或垂直）于同一直线的两直线__________。 ④平行线的性质：（1）经过直线外一点，有且只有________条直线与这条直线平行。 （2）两直线平行，同位角__________。 （3）两直线平行，内错角__________。 （4）两直线平行，同旁内角__________． （5）一条直线和两条平行线中的一条垂直（或平行），这条直线也和__________垂直（或 平行）． （6）平行线间的距离处处__________。 （7）经过三角形一边的中点与另一边平行的直线必平分__________。 考点透视 1、了解直线、线段和射线等概概念的区别，两条相交直线确定一个交点，了解 线段和与差及线段的中点、两点间的距离、角、周角、平角、直角、锐角、钝 角等概念，掌握两点确定一条直线的性质，角平分线的概念，度、分、秒的换 算，几何图形的符号表示法，会根据几何语句准确、整洁地画出相应的图形； 2、了解斜线、斜线段、命题、定义、公理、定理及平行线等概念，了解垂线段 最短的性质，平行线的基本性质，理解对顶角、补角、邻补角的概念，理解对 顶角的性质，同角或等角的补角相等的性质，掌握垂线、垂线段、点到直线的 距离等概念，会识辨别同位角、内错角和同旁内角，会用一直线截两平行线所 得的同位角相等、内错角相等、同旁内角互补等性质进行推理和计算，会用同 位角相等、内错角相等、或同旁内角互补判定两条直线平行。 一.填空题 1．平行线：在同一平面内，__________的两条直线叫做平行线。 2．在同一平面内，两条直线的位置关系只有两种：__________。相交时，对顶角相等。 3．平行线的判定： （1）同位角__________，两直线平行。 （2）内错角相等，两直线__________。 （3）同旁内角__________，两直线平行。 （4）平行（或垂直）于同一直线的两直线__________。 4.平行线的性质：（1）经过直线外一点，有且只有________条直线与这条直线平行。 （2）两直线平行，同位角__________。 （3）两直线平行，内错角__________。 （4）两直线平行，同旁内角__________． （5）一条直线和两条平行线中的一条垂直（或平行），这条直线也和__________ 垂直（或平行）． （6）平行线间的距离处处__________。 （7）经过三角形一边的中点与另一边平行的直线必平分__________。 5.两条直线相交，构成 对对顶角， 对邻补角。 6.如图 （1）∠BAO 与∠AOC 是由直线 、 被 所截的 角； （2）∠AOB 与∠BCD 是由直线 、 被 所截的 角； （3）∠B 与∠BCE 是由直线 、 被 所截的 角； （4）∠DAE 与∠AOC 是由直线 、 被 所截的 角； 7.如图，已知：AD∥BC，AB∥DE，DF∥AC， ∠OEC＝72O，∠OCE＝64O，那么∠B＝ ，∠F＝ ， ∠BAD＝ ，∠ADF＝ 。 8.如图，已知：l1∥l2, ∠1=70o, ∠2=65o. 则∠3＝ ，∠4＝ 。 9.把下列命题改成一般形式： A D B O C E A D O B E C F 4 1 l1 3 2 l2 （1） 同角的余角相等； ； （2） 平行线的内错角的平分线互相平行； 。 10.邻补角的平分线互相 。 11.如图，已知：AC⊥BC，DE⊥AC，CD⊥AB， 且∠CDE＝∠BGF。求证：GF⊥AB。 证明：∵BC⊥AC，DE⊥AC （ ） ∴∠ACB＝∠AED＝90O（ ） ∴DE BC （ ） ∴∠EDC＝∠ （ ） ∵∠CDE＝∠BGF （ ） ∴∠DCB＝∠BGF （ ） ∴ ∥ （ ） ∴∠BFG＝∠BDC （ ） ∵CD⊥AB（ ） ∴∠BDC＝90O（ ） ∴∠BFG＝90O（ ） ∴GF⊥AB（ ） E A G B F D C 12如图点O是直线AB上的一点，OC⊥OD，∠AOC-∠BOD＝20°,则∠AOC＝ 。 13．如图，∠１＝42°，则∠１＝ 0 14．如图∠１＝70°，∠２＝35°，则∠３＝ , ∠４＝ 。 15．两个角的两边互相平行，其中一个角是另一个角的３倍，则这两个角的度数分别是 和 。 16．现有一张长４０，宽２０的长方形纸片，要从中剪出长为１８，宽为１２的长方形纸片， 最多能剪出 张。 O D C BA 12 题图 c b a 13 题图 2 1 b a 14 题图 4 3 2 1 17．填写推理的理由： 已知，ＡＢ⊥ＭＮ，ＣＤ⊥ＭＮ，垂足为Ｂ、Ｄ，ＢＥ、ＤＦ分别平分， ∠ＡＢＮ，∠ＣＤＮ。 求证：∵ＡＢ⊥ＭＮ，ＣＤ⊥ＭＮ ∴∠ＡＢＤ＝∠ＣＤＮ＝90° ∵ＢＥ、ＤＦ分别平分∠ＡＢＮ、∠ＣＤＮ ∴∠１＝ ，∠２＝ （ ） ∴ ＝ ∴ＢＥ∥ＤＦ（ ） ∴∠Ｅ＋∠Ｆ＝180° 18.如图一个弯形管道ＡＢＣＤ的拐角∠ＡＢＣ＝１２０0，∠ＢＣＤ＝６０0，这时说管道Ａ Ｂ∥ＣＤ，是根据 1９.如图直线ＡＢ、ＣＤ、ＥＦ相交于点Ｏ，是∠ＡＯＣ的邻补角是 ，∠ＤＯ Ａ的对顶角是 ，若∠ＡＯＣ＝５０0，则 ∠ＢＯＤ＝0，∠ＣＯＢ＝ 0 20.如图所示的长方体，用符号表示下列棱的位置关系： A1B1 AB AA1 AB1，A1D1 C1D1 AD BC 21.如图直线，a∥b,∠1=540，则∠2= 0，∠3= 0，∠4= 0。 22.命题“同角的余角相等”的题设是 ， 结论是 。 23.如图 OC⊥AB，DO⊥OE，图中与∠1 与 互余的角是 ，若∠COD=600， 则∠AOE= 0。 NM 21 FE D C B A 18 题图 D C BA O 19 题图 F E D C BA D1 C1 B1 A1 20 题图 D C BA 21 题图 b a 43 2 1 O 23 题图 ED C BA NM 24 题图 F E D C BA 24.如图直线 AB 分别交直线 EF，CD 于点 M，N 只需添一个条件 就可得 到 EF∥CD。 25．如图，a 与 b 直线相交，∠1=36０，则∠3=________，∠2=__________ 26．如图，直线 AB、CD、EF 相交于点 O，则∠AOC 的对顶角是_____________，∠AOD 的对顶角是_____________ 27．在同一平面内，两条直线的位置关系只有两种_________ 28．命题“两直线平行，内错角相等”的题设_________，结论____________ 29．如图，要从小河 a 引水到村庄 A，请设计并作出一最佳路线，理由是：__________ 30．如图，∠1=70０，a∥b 则∠2=_____________， 31．如图，若∠1=∠2，则互相平行的线段是________________ 32.如图，若 AB⊥CD，则∠ADC=____________， 33．如图，a∥b,∠1=118０，则∠2=___________ 34．如图∠B 与∠_____是直线______和直线_______被直线_________所截的同位角。 35.两条直线相交最多有 个交点，三条直线相交最多有 个交点，四条直线相交 最多有 个交点。 3６．一个角的补角比这个角的余角大 度。 3７．５个同学互相握手，共握_________次。 38．如图所示，有一个破损的扇形零件，利用图中的量角器可以量出这个扇形的圆心角的度 数，所用的数学依据是 ； 3 2 1 25 题图 b a O 26 题图 FE D C B A 29 题图 A 2 1 30 题图 ba 2 1 31 题图 D C BA 32 题图 D C BA 2 1 33 题图 c b a 34 题图 F CB A 39．如图，光线 a 照射到平面镜 CD 上，然后在平面镜 AB 和 CD 之间来回反射，这时光线 入射角等于反射角，即∠1＝∠6，∠5＝∠3，∠2＝∠4。若已知∠1=55°，∠3=75°，那 么∠2 等于 。 40、用尺规作图时，用 画直线、射线和直线，用 画弧或圆。 41、黎老师家在小星家的北偏东 68 度，则小星家在黎老师家的南偏西 度 。 42、如图①，如果∠ ＝ ∠ ，可得 AD∥BC，你的根据是 。 43、如图②，∠1 = 82º，∠2 ＝ 98º，∠3 = 80º，则∠4 ＝ 度。 44、如图③，直线 AB，CD，EF 相交于点 O，AB⊥CD，OG 平分∠AOE， ∠FOD = 28º，则∠BOE = 度，∠AOG = 度。 45、一个角与它的补角之差是 20º，则这个角的度数是 度。 46、如图④，AB∥CD，∠BAE = 120º，∠DCE = 30º，则∠AEC = 度。 47、如图⑤，OA⊥OB，OC⊥OD，O 是垂足，∠BOC=55º，那么∠AOD= . 48、如图⑥中∠DAB 和∠B 是直线 DE 和 BC 被直线 所截而成的，称它们为 角。 O F E D C B A O E D C B A O 4 3 2 1 D C B A 49、把一张长方形纸条按图⑦中，那样折叠后，若得到∠AOB′= 70º，则∠B′OG = 。 50．自钝角的顶点引角的一边的垂线，把这个钝角分成两个角的度数之比是 3∶1，则这个 钝角的度数是___________． 51．如图 BE，CF 相交于 O，OA，OD 是射线，其中构成对顶角的角是____________ （第 51 题图） （第 52 题图） 52．如图，直线 AB，CD 相交于 O，OE 平分∠AOC，∠EOC=35°，则∠BOD=___________． 53．如图，直线 AB 和 CD 相交于点 O，则∠3 的对顶角是 ，∠2 的邻补角是 ， 若∠2=120°，则 ∠1= ，∠4= . 54. 在同一平面内，不重合的两条直线的位置关系只有____________。 55. 如图（1），直线 AB、CD、EF 相交于 O 点，则∠AOC 的对顶角是________， ∠DOE 的邻补角是_____________。 56. 直线 AB、CD 相交于 O 点,若∠AOC = 30°,则∠AOD = _____。 57. 点到直线的距离是直线外一点到这条直线的_____________。 58. 如图（2），AB⊥CD，∠1 = 30°，则∠2 = _____。 A BC D (3) · A B1 2 C D (2) A B C D E F O (1) 59. 如图（3），计划把河水引到村庄 A，先引 AB⊥CD， 垂足为 B，然后沿 AB 开渠，能使所开的渠道最短， 这样设计的依据是__________________。 60. 在同一平面内 a⊥b，c⊥b，则 a____c。 61. 如图（4），若 a∥b，∠1 = 50°，则∠2 = _____。 62. 如图（5），若∠1 =∠2，则_____∥_____。 63. 如图（6）：AB∥CD∥EF，则∠BAC+∠ACE+∠CEF = ________. 二.选择题 1、如果一个角的补角是 150°，那么这个角的度数是（ ） A. 30° B. 60° C.90° D.120° 2、如图，已知直线 a、b 被直线 c 所截，a∥b，∠1＝130°，则 ∠2＝（ ） A. 130° B. 50° C.40° D.60° 3、下列说法错误的是( ) Ａ.内错角相等，两直线平行． Ｂ.两直线平行，同旁内角互补． C.相等的角是对顶角． D.等角的补角相等． 4、下列图中∠1 和∠2 是同位角的是（ ） A. ⑴、⑵、⑶， B. ⑵、⑶、⑷， C. ⑶、⑷、⑸， D. ⑴、⑵、⑸ 5、已知:如图, ∠1＝∠2 , 则有( ) A.AB∥CD B.AE∥DF C. AB∥CD 且 AE∥DF D.以上都不对 6、如图,直线 AB 与 CD 交于点 O,OE⊥AB 于 O,图∠1 与∠2 的关系是( ) A.对顶角 B.互余 C.互补 D 相等 7、如图，DH∥EG∥BC，且 DC∥EF，那么图中和∠1 相等的角的个数是（ ） A.2， B. 4， C. 5， D. 6 1 2 A B C D(5) A C E F D B (6) 1 2 b a (4) 8、如图，AB//CD，BC//DE，则∠B+∠D的值为（ ） A.90° B.150° C.180° D. 以上都不对 9、如图，直线AB与CD相交于点O，OB平分∠DOE.若∠DOE＝60 º， 则∠AOE的度数是（ ） A.90° B.150° C.180° D. 不能确定 10、一束光线垂直照射在水平地面，在地面上放一个平面镜，欲使这束光线经过平面镜反射 后成水平光线，则平面镜与地面所成锐角的度数为（ ） A.45º B.60º C.75º D.80º 11．命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④ 同 位角相等。 其中错误的有（ ） Ａ、1 个 Ｂ、２个 Ｃ、３个 Ｄ、４个 12．如图 直线ＡＢ、ＣＤ相交于点Ｏ，ＯＥ⊥ＡＢ于Ｏ，∠DOE＝55°， 则∠AOC 的度数为（ ） Ａ、40° Ｂ、45° Ｃ、30° Ｄ、35° 13.如图两条非平行的直线 AB，CD 被第三条直线 EF 所截，交点为 PQ，那么这条直线将所 在平面分成（ ） A、5 个部分 B、6 个部分 C、7 个部分 D、8 个部分 O 12 题图 E D C B A P 13 题图 Q F E D C BA 14 题图 DC BA 5 15 题图 L2 L1 4 3 21 1４．如图ＡＢ∥ＣＤ，ＡＣ⊥ＢＣ，图中与∠ＣＡＢ互余的角有（ ） Ａ、１个 Ｂ、２个 Ｃ、３个 Ｄ、４个 15．如图下列条件中，不能判断直线的是（ ） Ａ、∠１＝∠３ Ｂ、∠２＝∠３ Ｃ、∠４＝∠５ Ｄ、∠４＋∠２＝180° 16．如图已知∠１＝∠２，∠ＢＡＤ＝∠ＢＣＤ，则下列结论⑴ＡＢ∥ＣＤ ⑵ＡＤ∥ＢＣ，⑶∠Ｂ＝∠Ｄ，⑷∠Ｄ=∠ＡＣＢ，正确的有（ ） Ａ、１个 Ｂ、２个 Ｃ、３个 Ｄ、４个 17.如果两条直线被第三条直线所截，那么一组内错角的平分线（ ） Ａ、互相垂直 Ｂ、互相平行 Ｃ、互相重合 Ｄ、 以上均不正确 18 如图已知∠１＋∠３＝180°，则图中与∠１互补的角还有（ ） Ａ、１个 Ｂ、２个 Ｃ、３个 Ｄ、４个 19．在下图中，∠1,∠2 是对顶角的图形是（ ） 20．若 a⊥b，c⊥d 则 a 与 c 的关系是（ ） A、 平行 B、垂直 C、 相交 D、以上都不对 21．下列语句中，正确的是（ ） A、相等的角一定是对顶角 B、互为补角的两个角不相等 C、两边互为反向处长线的两个角是对顶角 D、交于一点的三条直线形成 3 对对顶角 22．下列语句不是命题的是（ ） A、 明天有可能下雨 B、同位角相等 C、∠A 是锐角 D、 中国是世界上人口 最多的国家 23．下列语句中，错误的是（ ） A、一条直线有且只有一条垂线 B、不相等的两个角不一定是对顶角， C、直角的补角必是直角 D、两直线平行，同旁内角互补 24．如图，不能推出 a∥b 的条件是（ ） A 2 1 21 B 2 1 C 2 1 D 16 题图 2 1 D C BA 87 65 18 题图 4 32 1 4 3 2 1 c b a A、∠1=∠3 B、∠2=∠4 C、∠2=∠3 D、∠2+∠3=1800 25．如图 a∥b,∠1 与∠2 互余，∠3=1150，则∠4 等于（ ） A、 115０ B、 155０ C、 135０ D、125０ 26．如图，∠1=15０ , ∠AOC=90０，点 B、O、D 在同一直线上，则∠2 的度数为（ ） A、75０ B、15０ C、105０ D、 165０ 27、如图，能表示点到直线（或线段）距离的线段有（ ） A、 2 条 B、3 条 C、4 条 D、5 条 28.如果角的两边有一边在同一条直线上，另一边互相平行，则这两个角 A．相等 B．互补 C．相等且互补 D．相等或互补 29．下列命题中的真命题是 A．在所有连结两点的线中，直线最短。 B．经过两点有一条直线，并且只有一条直线 C．内错角互补，则两直线平行 D．如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直 30.如图，点 E 在 BC 的延长线上，在下列四个条件中，不能判定 AB∥CD 的是( ) A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180° 4 3 2 1 A E C D B 31. 一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐 弯的角度是（ ） A．第一次右拐 50°，第二次左拐 130° B．第一次左拐 50°，第二次右拐 50° C．第一次左拐 50°，第二次左拐 130° D．第一次右拐 50°，第二次右拐 50° 32. 如图，AB∥CD，那么∠A，∠P，∠C 的数量关系是( ) A.∠A+∠P+∠C=90° B.∠A+∠P+∠C=180° C.∠A+∠P+∠C=360° D.∠P+∠C=∠A d 25 题图 4 3 2 1 c b a O 26 题图 D C B A 2 1 27 题图 D C BA D A P C B 33 下列说法中，正确的个数是（ ） （1） 相等且互补的两个角都是直角． （2） 互补角的平分线互相垂直． （3） 邻补角的平分线互相垂直． （4） 一个角的两个邻补角是对顶角． （Ａ）１． （Ｂ）２． （Ｃ）３． （Ｄ）４． 34.下列图中，∠1 与∠2 是对顶角（ ） 35 如图（7），一条公路两次转弯后又回到原来的方向（即 AB∥CD），如果第一次转弯时的∠ B = 140°，那么∠C 是（ ） A. 40° B. 140° C. 100° D. 180° 36.下列说法中正确的是（ ） A. 同位角相等 B. 过一点有且只有一条直线与已知直线平行 C. 两条直线不相交是平行 D. 若 a∥b，a∥c，则 b∥c 37.∠1 和∠2 是直线 a、b 被直线 c 所截的内错角，则∠1 与∠2 大小关系是（ ） A. ∠1 = ∠2 B. ∠1﹥∠2 C. ∠1 和∠2 D. 无法确定 38.如图（8），∠BAC = 90°，AD⊥BC，垂足为 D，则点 A 到 BC 的距离是线段（ ） A. BC B. AD C. AC D. BD 39.如图（9）直线 AB、CD 相交于点 O，OE⊥CD，O 为垂足，若∠EOB = 52°，则∠AOC 的 度数是（ ） A. 38° B. 52° C. 90° D. 128° 三、解答题： 1.如图ＡＢ∥ＣＤ，∠NCM＝90°，∠NCB＝30°，CM 平分∠BCE，求∠B 的大小（10 分）。 E N M C D BA 2 A 2 D2B 2 C A B C D (7) A B C D O E (9) A B CD(8) 2.对于同一平面的三条直线，给出下列５个论断: ①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件，一个论断为结论，组成一个你 认为正确的命题（8 分） 已知： ,结论 . 理由： 3.如图已知∠１＝∠２，再添上什么条件，可使ＡＢ∥ＣＤ成立（至少写出四组条件，其中 每一组条件均能使ＡＢ∥ＣＤ成立）？并说明理由（10 分） 4.如图已知ＡＢ、ＢＥ、ＥＤ、ＣＤ依次相交于Ｂ、Ｅ、Ｄ， ∠Ｅ＝∠Ｂ＋∠Ｄ。试说明ＡＢ∥ＣＤ. 5.根据题意，画出图形，写出已知、求证：（不要求证明，能独立完成证明者可获加公） 平行线的内错角的平分线互相平行。 6.如图：已知 AB∥CD，∠A＝ 2 1 ∠D。求∠A、∠D。 D C A B 21 E NM C F DB A E C D BA 7.如图 ① 若∠1=∠2 则 ∥ （ ） 若∠DAB+∠ABC=1800 则 ∥ （ ） ② 当 ∥ 时 ∠ C+∠ABC=1800 （ ） 当 ∥ 时 ∠3=∠C （ ） 8.：如图ＡＢ∥ＣＤ，ＥＦ交ＡB 于 G，交 CD 于 F，FH 平分∠EFD，交 AB 于 H ，∠AGE=500 （10 分） 求：∠BHF 的度数。 9.∠1=300，∠B=600，AB⊥AC（10 分） ① ∠DAB+∠B= 0 ② AD 与 BC 平行吗？AB 与 CD 平行吗？ 试说明理由。 10.已知：如图 AE⊥BC 于点 E，∠DCA=∠CAE， 试说明 CD⊥BC 3 2 1D C BA H G F E DC BA 1 D CB A 11.已知：如图∠1=∠2，∠C=∠D，∠A=∠F 相等吗？试说明理由 12.如图，直线 CD 与直线 AB 相交于 C，根据下列语句画图 （1）过点 P 作 PQ∥CD，交 AB 于点 Q （2）过点 P 作 PR⊥CD，垂足为 R （3）若∠DCB=120０，猜想∠PQC 是多少度？并说明理由 13.填写推理理由（1′×15） （1） 已知：如图，D、E、F 分别是 BC、CA、AB 上的点，D∥AB，DF∥AC 试说明∠ FDE=∠A 解：∵DE∥AB（ ） ∴∠A+∠AED=180０ （ ） ∵DF∥AC（ ） E D CB A H G 2 1 FED CBA P D C BA FE D CB A ∴∠AED+∠FED=180０ （ ） ∴∠A=∠FDE（ ） （2） 如图 AB∥CD ∠1=∠2，∠3=∠4，试说明 AD∥BE 解：∵AB∥CD（已知） ∴∠4=∠_____（ ） ∵∠3=∠4（已知） ∴∠3=∠_____（ ） ∵∠1=∠2（已知） ∴∠ 1+∠CAF=∠2+∠CAF（ ） 即 ∠_____ =∠_____（ ） ∴∠３＝∠_____ ∴ＡＤ∥ＢＥ（ ） 14．已知：如图，AB⊥CD，垂足为 O ，EF 经过点 O，∠２＝４∠１， 求∠２，∠３，∠ＢＯＥ的度数（１０′） 15.如图：已知；ＡＢ∥ＣＤ，ＡＤ∥ＢＣ，∠Ｂ与∠Ｄ相等吗？试说明理由。（１０′） 16.如图：在三角形ＡＢＣ中，∠ＢＣＡ＝９００，ＣＤ⊥ＡＢ于点 D，线段ＡＢ、ＢＣ、Ｃ Ｄ的大小顺序如何？并说明理由。 F E D CB A 4 3 2 1 F E O D C BA 3 2 1 D C BA D C BA 17．已知：如图 AOC 与 BOD 为对顶角，OE 平分 AOC，OF 平分 BOD. 求证：OE、OF 互为反向延长线 18．已知：如图 AB // CD，AD // BC。 求证： A =  C， B =  D 19．如图，已知：  ABC 和  CBD 互为邻补角，BE 平分  ABC，BF 平分  CBD。 求证： BE BF 。 20．已知： AD BC EF BC    , , 1 2 求证： DG BA/ / B D E 1 3 A C F 2 21．已知；如图 AB // ED 求证 B +  BCD +  D = 360° 22.已知 AD⊥BC，FG⊥BC，垂足分别为 D、G，且∠1=∠2，猜想∠BDE 与∠C 有怎样的大小关 系？试说明理由. 23. 如图，已知直线 l1∥l2，直线 l3 和直线 l1、l2 交于点 C 和 D，在 C、D 之间有一点 P，如 果 P 点在 C、D 之间运动时，问∠PAC，∠APB，∠PBD 之间的关系是否发生变化.若点 P 在 C、D 两点的外侧运动时（P 点与点 C、D 不重合），试探索∠PAC，∠APB，∠PBD 之间 的关系又是如何？ l1 l C B D P l2 A 24.完成推理填空：如图：直线 AB、CD 被 EF 所截，若已知 AB//CD，求证：∠1 ＝ ∠C 。 请你认真完成下面填空。 证明：∵ AB//CD（已知）， ∴∠1 ＝ ∠ （ 两直线平行， ） 又∵∠2 ＝ ∠3， （ ） ∴∠1 ＝ ∠C （ ）。 25.完成推理填空：如图：已知∠A＝∠F，∠C＝∠D，求证：BD∥CE 。 请你认真完成下面的填空。 证明：∵∠A＝∠F （ 已知 ） ∴AC∥DF （ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ ） ∴∠D＝∠ （ ＿＿＿＿＿＿＿＿＿＿＿＿＿ ） 又∵∠C＝∠D （ 已知 ）， ∴∠1＝∠C （ 等量代换 ） ∴BD∥CE（ ）。 26.如图：已知∠B＝∠BGD，∠DGF＝∠F，求证：∠B ＋ ∠F ＝180°。 请你认真完成下面的填空。 证明：∵∠B＝∠BGD （ 已知 ） ∴AB∥CD （ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ ） ∵∠DGF＝∠F；（ 已知 ） ∴CD∥EF （ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ ） ∵AB∥EF （ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ ） ∴∠B ＋ ∠F ＝180°（ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ ）。 27.如图：已知 AB∥A′B′，BC∥B′C′，那么∠B 与∠B′有何关系？为什么？ 28.如图：a∥b，∠1=122°，∠3=50°，求∠2 和∠4 的度数 。 4 3 2 1 b a 29.如图 ，已知 AB∥CD，∠ABE 和∠CDE 的平分线相交于 F，∠E = 140º， 求∠BFD 的度数？ 30.如图，已知 1 2, 3 4 180        ，求证： 5 6   3 1 2 5 4 6 31.如图，已知 AD ∥ BC ， DFE C   ，求证： AD ∥ EF A D E F B C 32 如图， AB 与 CD 交于点 O ， ,A COA B BOD      ，求证： AC ∥ BD A D O C B 33.如图， 180B D     ，AE、CE 分别平分 ,BAC DCA  ，求证： AE CE A B E C D 34 如图， oc 平分 ,AOB DC ∥OB ，求证： DO DC A D C  B 35 如图１－５，已知 AD//BC，∠1=∠2，∠A=112°，且 BD⊥CD，则∠ABC=_____，∠C=_____. 36 已知：如图 AC 平分∠DAB，∠1 =∠2，问：AB 平行 CD 吗？为什么？ A D C B 1 2 37 如图，AD 是∠EAC 的平分线，AD∥BC，∠B = 30°，求∠C 的度数。 38 如图，已知∠AMB=∠EBF，∠BCN=∠BDE，求证：∠CAF=∠AFD． 39.如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角 A 是 120°，第二次 拐的角 B 是 150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行， 问∠C 是多少度？说明你的理由． 40．（1）如图，若 AB∥DE，∠B=135°，∠D=145°，你能求出∠C 的度数吗？ （2）在 AB∥DE 的条件下，你能得出∠B、∠C、∠D 之间的数量关系吗？并说明理由． A B C D E 41 如图，在折线 ABCDEFG 中，已知∠1=∠2=∠3=∠4=∠5，延长 AB、GF 交于点 M．试探索 ∠AMG 与∠3 的关系，并说明理由． 42 已知如图，四边形 ABCD 中，AB∥CD，BC∥AD，那么∠A 与∠C，∠B 与∠D 的大小关系如 何？请说明你的理由． 43.如图：直线 AB、CD 相交于点 O，∠EOC = 80°，OA 平分∠EOC，求:∠BOD 的度数。 AB O C ED · 44.如图 AB⊥CD，垂足为 O，EF 经过点 O，∠1 = 25°，求:∠2，∠13，∠EOB 的度数。 45.已知：线段 AB 及线段 AB 外一点 P （1）过点 P 作线段 AB 的垂线 PD，垂足为 D （2）过点 P 作 PE∥AB A B C D E F 3 2 1 O