人教版7年级下册数学全册教案第17课时 6_1平方根（第2课时）

人教版7年级下册数学全册教案第17课时 6_1平方根（第2课时）

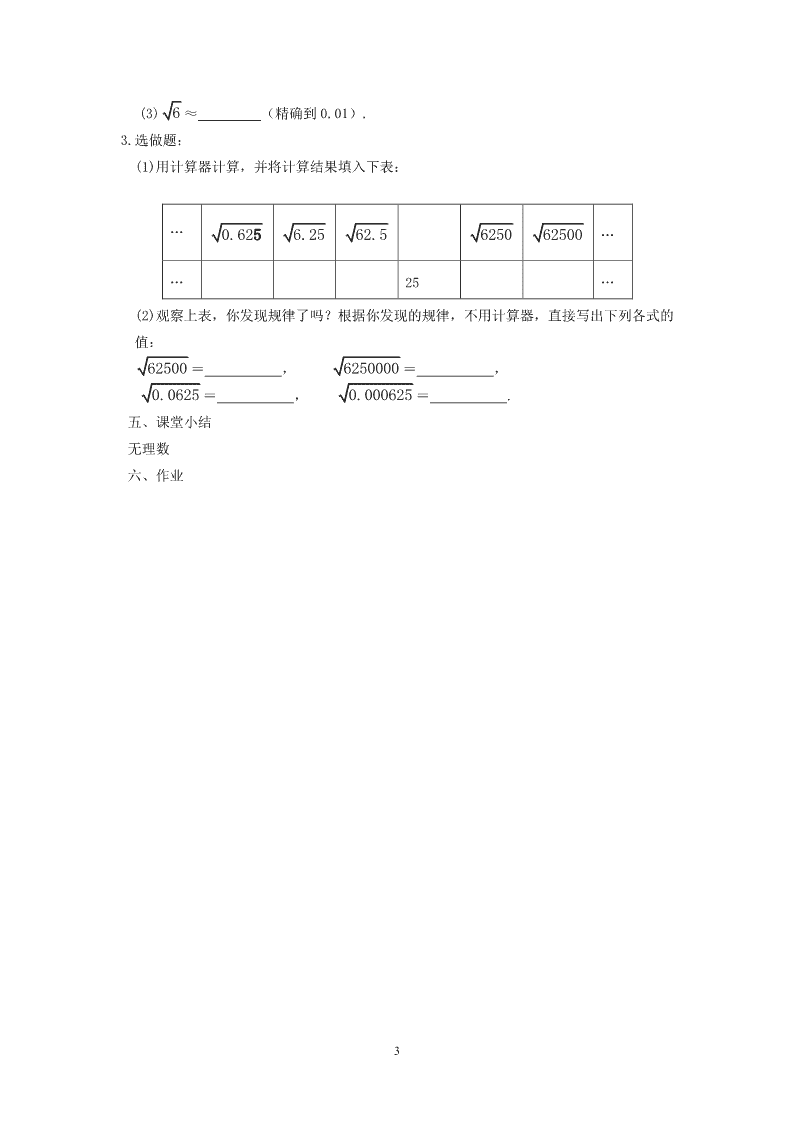
1 6 .1 平方根（第 2 课时） 一、教学目标 1.通过由正方形面积求边长，让学生经历 2 的估值过程，加深对算术平方根概念的理解， 感受无理数，初步了解无限不循环小数的特点. 2.会用计算器求算术平方根. 二、重点和难点 1.重点：感受无理数. 2.难点：感受无理数. （本节课使用计算器，最好每个同学都要有计算器） 三、合作探究 1.填空：如果一个正数的平方等于 a，那么这个正数叫做 a 的_______________，记作_______. 2.填空： (1)因为_____2＝36，所以 36 的算术平方根是_______，即 36 ＝_____； (2)因为(____)2＝ 9 64 ，所以 的算术平方根是_______，即 9 64 ＝_____； (3)因为_____2＝0.81，所以 0.81 的算术平方根是_______，即 0.81 ＝_____； (4)因为_____2＝0.572，所以 0.572 的算术平方根是_______，即 20.57 ＝_____. 3.师抽卡片生口答. （课前制作若干张卡片，一面是 a 的形式，一面是算术平方根的值，卡片中要包括 121 到 361 ，还要包括被开方数是分数、小数、a2 等形式） （二） （看下图） 这个正方形的面积等于 4，它的边长等于多少？ 谁会用算术平方根来说这个正方形边长和面积的关系？ 这个正方形的面积等于 1，它的边长等于多少？ 用算术平方根来说这个正方形边长和面积的关系？ （指准图）这个正方形的边长等于面积 1 的算术平方根，也就是边长＝ 1 （边讲边板书： 边长＝ ）. 等于多少？ 生：等于 1.（师板书：＝1） （看下图）这个正方形的面积等于 2，它的边长等于什么？（稍停） 因为边长等于面积的算术平方根，所以边长等于 2 面积＝4 面积＝1 面积＝2 2 （板书：边长＝ 2 ）.（上面三个图的位置如下所示） 4 ＝2， 1 ＝1，那么 等于多少呢？（在 后板书：＝？）求 等于多少，怎么求？ 在 1 和 2 之间的数有很多，到底哪个数等于 呢？我们怎么才能找到这个数呢？我们可以 这样来考虑问题，等于 的那个数，它的平方等于多少？ 第一条线索是那个数在 1 和 2 之间，第二条线索是那个数的平方恰好等于 2.根据这两条线 索，我们来找等于 的那个数. 我们在 1 和 2 之间找一个数，譬如找 1.3，（板书：1.32＝）1.3 的平方等于多少？（师生共 同用计算器计算） 1.69 不到 2，说明 1.3 比我们要找的那个数小.1.3 小了，那我们找 1.5，1.5 的平方等于多 少？（师生共同用计算器计算）2.25 超过 2，说明 1.5 比我们要找的那个数大.找 1.3 小了， 找 1.5 又大了，下面怎么找呢？大家用计算器，算一算，找一找，哪个数的平方恰好等于 2？ 等于 1.41421356 点点点，可见是一个小数，这个小数与我们以前学过的小数相比有点 不同，有什么不同呢？第一，这个小数是无限小数（板书：无限）. 是无限小数，又是 不循环小数，所以 是一个无限不循环小数. 除了 ，还有别的无限不循环小数吗？无限不循环小数还有很多很多， 3 、 5 、 6 、 7 都是无限不循环小数（板书： 、 、 、 都是无限不循环小数）. 那怎么求 、 、 、 这些无限不循环小数的值呢？我们可以利用计算器来求.四、 精讲精练 例 用计算器求下列各式的值： (1) （精确到 0.001）； (2) 3136 . （按键时，教师要领着学生做；解题格式要与课本上的相同） 练习 1.填空： (1)面积为 9 的正方形，边长＝ ＝ ； (2)面积为 7 的正方形，边长＝ ≈ （利用计算器求值，精确到 0.001）. 2.用计算器求值： (1) 1849 ＝ ； (2) 86.8624 ＝ ； 边长＝ 4＝2边长＝ 2边长＝ 1＝1 面积＝2面积＝1 面积＝4 3 (3) 6 ≈ （精确到 0.01）. 3.选做题： (1)用计算器计算，并将计算结果填入下表： … 0.625 6.25 62.5 6250 62500 … … 25 … (2)观察上表，你发现规律了吗？根据你发现的规律，不用计算器，直接写出下列各式的 值： ＝ ， 6250000 ＝ ， 0.0625 ＝ ， 0.000625 ＝ . 五、课堂小结 无理数 六、作业