- 2021-07-01 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【百强校】甘肃省兰州市第一中学2019届高三6月最后高考冲刺模拟数学(理)试题(含答案解析)
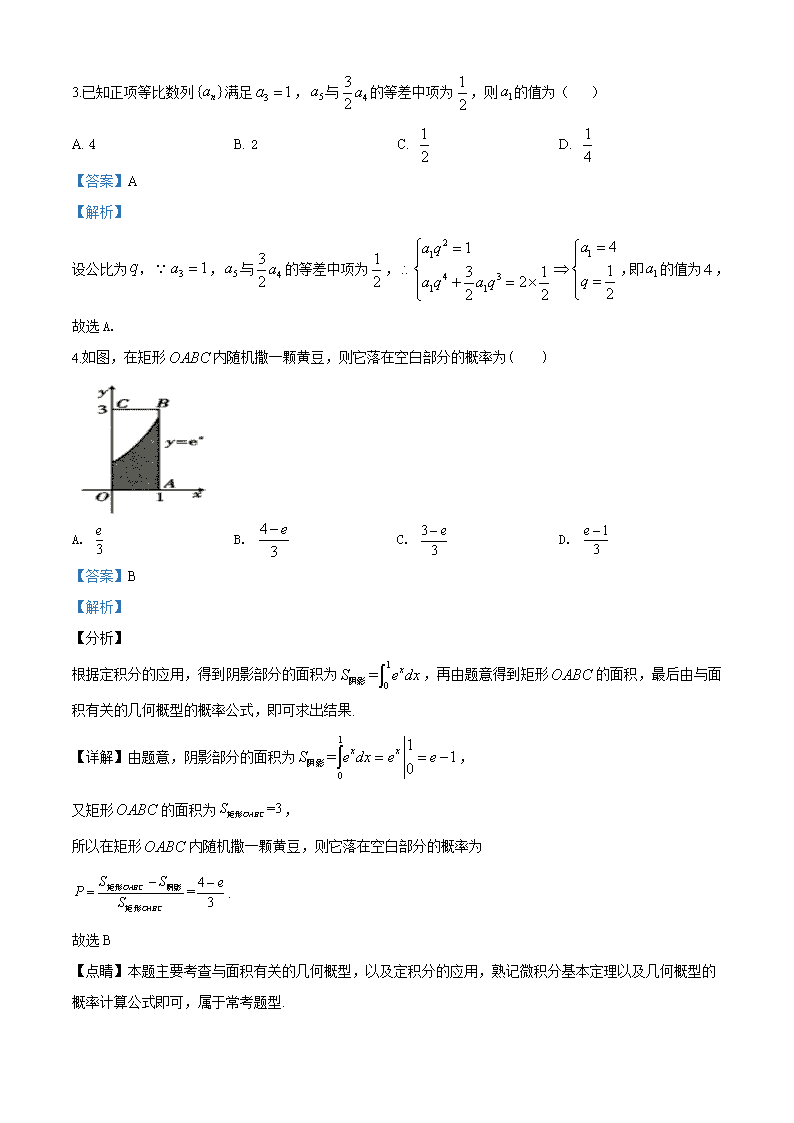
兰州一中 2019 届高三冲刺模拟试题 数学(理科) 第Ⅰ卷(选择题 共 60 分) 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一 项是符合题目要求的) 1.已知集合 A= ,则 =( ) A. (2,6) B. (2,7) C. (-3,2] D. (-3,2) 【答案】C 【解析】 【分析】 由题得 ={x|x≤2 或 x≥7},再求 得解. 【详解】由题得 ={x|x≤2 或 x≥7},所以 . 故选 C 【点睛】本题主要考查集合的运算,意在考查学生对这些知识的理解掌握水平和分析推理能力. 2.已知复数 对应复平面上的点 ,复数 满足 ,则 ( ) A. B. C. D. 【答案】D 【解析】 【分析】 先由题意得到 ,再由 求出 ,根据复数模的计算公式,即可求出结果. 【详解】因为复数 对应复平面上的点 ,所以 , 又复数 满足 , 所以 , 因此 . 故选 D 【点睛】本题主要考查复数的模的计算,熟记复数的运算法则以及复数的几何意义即可,属于基础题型. { | 3 6}, { | 2 7}x x B x x− < < = < < ( )RA B C B∪ ( )A C B∪∩ C B∪ ( )A C B∪∩ = ( ]3,2− 1z ( 1,1)− 2z 1 2 2z z = − 2 2iz + = 2 2 10 10 1 1z i= − + 1 2 2z z = − 2z 1z ( 1,1)− 1 1z i= − + 2z 1 2 2z z = − 2 1 2 2 2 2(1 ) 11 1 (1 )(1 ) iz iz i i i i − − += = = = = +− + − − + 2 2i 1 3 10z i+ = + = 3.已知正项等比数列 满足 , 与 的等差中项为 ,则 的值为( ) A. 4 B. 2 C. D. 【答案】A 【解析】 设公比为 , , 与 的等差中项为 , ,即 的值为 , 故选 A. 4.如图,在矩形 内随机撒一颗黄豆,则它落在空白部分的概率为( ) A. B. C. D. 【答案】B 【解析】 【分析】 根据定积分的应用,得到阴影部分的面积为 ,再由题意得到矩形 的面积,最后由与面 积有关的几何概型的概率公式,即可求出结果. 【详解】由题意,阴影部分的面积为 , 又矩形 的面积为 , 所以在矩形 内随机撒一颗黄豆,则它落在空白部分的概率为 . 故选 B 【点睛】本题主要考查与面积有关的几何概型,以及定积分的应用,熟记微积分基本定理以及几何概型的 概率计算公式即可,属于常考题型. { }na 3 1a = 5a 4 3 2 a 1 2 1a 1 2 1 4 q 3 1a = 5a 4 3 2 a 1 2 2 11 4 3 1 1 41 13 12 22 2 aa q qa q a q = = ∴ ⇒ =+ = × 1a 4 OABC 3 e 4 3 e− 3 3 e− 1 3 e − 1 0 = xS e dx∫阴影 OABC 1 0 1= 10 x xS e dx e e= = −∫阴影 OABC =3OABCS矩形 OABC 4= 3 OABC OABC S S eP S − −= 阴影矩形 矩形 5.已知命题 ,命题 ,且 ,则( ) A. 命题 是真命题 B. 命题 是假命题 C. 命题 是假命题 D. 命题 是真命题 【答案】A 【解析】 【分析】 先分别判断命题 与命题 的真假,进而可得出结果. 【详解】令 ,则易知 在 上单调递增, 所以当 时, ,即 ; 因此命题 为真命题; 由 得 ; 所以,当 时, ;当 时, ; 因此,命题 ,且 为假命题; 所以命题 是真命题. 故选 A 【点睛】本题主要考查简单的逻辑连接词,复合命题真假的判定,熟记判定方法即可,属于常考题型. 6.7 人乘坐 2 辆汽车,每辆汽车最多坐 4 人,则不同的乘车方法有( ) A. 35 种 B. 50 种 C. 60 种 D. 70 种 【答案】D 【解析】 分析】 根据题意,分 2 步分析,①先将 7 人分成 2 组,1 组 4 人,另 1 组 3 人;②将分好的 2 组全排列,对应 2 辆汽车,由分步计数原理计算可得答案. 【详解】解:根据题意,分 2 步分析, ①,先将 7 人分成 2 组,1 组 4 人,另 1 组 3 人,有 C74=35 种分组方法, ②,将分好的 2 组全排列,对应 2 辆汽车,有 A22=2 种情况, 则有 35×2=70 种不同的乘车方法; 故选 D. 【 : ,2 xp x R x e∃ ∈ − > :q a R+∀ ∈ 21,log ( 1) 0aa a≠ + > p q∧ ¬ p q∨ ¬ p q∨ p q∧ p q ( ) xf x e x= + ( ) xf x e x= + R 0x < ( ) 1 2xf x e x= + < < 2xe x< − : ,2 xp x R x e∃ ∈ − > 0a > 2 1 1a + > 1a > 2log ( 1) 0a a + > 0 1a< < 2log ( 1) 0a a + < :q a R+∀ ∈ 21,log ( 1) 0aa a≠ + > p q∧ ¬ 【点睛】排列组合的综合应用问题,一般按先选再排,先分组再分配的处理原则.对于分配问题,解题的 关键是要搞清楚事件是否与顺序有关,对于平均分组问题更要注意顺序,避免计数的重复或遗漏. 7.将函数 的图象向右平移 个单位长度得到 图象,则下列判断正确的是( ) A. 函数 在区间 上单调递增 B. 函数 图象关于直线 对称 C. 函数 在区间 上单调递减 D. 函数 图象关于点 对称 【答案】ABD 【解析】 【分析】 根据图像变换的知识求得 解析式,由此判断 的单调性和对称性,确定正确选项. 【 详 解 】 函 数 的 图 像 向 右 平 移 个 单 位 长 度 得 到 . 由于 ,故 是 的对称轴,B 选项正确. 由于 ,故 是 的对称中心,D 选项正确. 由 ,解得 ,即 在区间 上递增,故 A 选项正确、C 选项错误. 故选:ABD. 【点睛】本小题主要考查三角函数图像变换,考查三角函数的对称性和单调性,属于基础题. 8.已知非零向量 , 的夹角为 ,且满足 ,则 的最大值为( ) A. B. C. D. ( ) sin 2 3f x x π = + 2 π ( )g x ( )g x ,12 2 π π ( )g x 7 12x π= ( )g x ,6 3 π π − ( )g x ,03 π ( )g x ( )g x ( ) sin 2 3f x x π = + 2 π ( ) π πsin 2 2 3g x x = − + 2πsin 2 3x = − 7π 7π 2π πsin sin 112 6 3 2g = − = = 7π 12x = ( )g x π 2π 2πsin sin 0 03 3 3g = − = = ,03 π ( )g x π 2π π22 3 2x− ≤ − ≤ π 7π 12 12x≤ ≤ ( )g x π 7π,12 12 a b 60 2 2a b− = a b⋅ 1 2 1 2 3 【答案】B 【解析】 【分析】 根据 得到 ,再由基本不等式得到 ,结 合数量积的定义,即可求出结果. 【详解】因为非零向量 , 的夹角为 ,且满足 , 所以 , 即 ,即 , 又因为 ,当且仅当 时,取等号; 所以 ,即 ; 因此, . 即 的最大值为 . 故选 B 【点睛】本题主要考查向量的数量积与基本不等式,熟记向量数量积的运算与基本不等式即可,属于常考 题型. 9.榫卯是我国古代工匠极为精巧的发明,它是在两个构件上采用凹凸部位相结合的一种连接方式.榫卯结构 中凸出部分叫榫(或叫榫头),已知某“榫头”的三视图如图所示,则该“榫头”的体积是( ) A. 36 B. 45 C. 54 D. 63 【答案】C 2 2a b− = 22 4 2 4a b a b+ − = 222 4 2 4a b a b a b≤ + − = a b 60 2 2a b− = 2 222 4 4 4a b a b a b− = + − ⋅ = 22 4 4 cos60 4a b a b+ − = 22 4 2 4a b a b+ − = 22 4 4a b a b+ ≥ 2a b= 222 4 2 4a b a b a b≤ + − = 2a b ≤ 1cos60 12a b a b a b⋅ = = ≤ a b⋅ 1 【解析】 【分析】 根据三视图还原该几何体,得到该几何体为两个相同的四棱柱拼接而成,再由题中数据,即可求出结果. 【详解】由三视图还原该几何体如下: 可得,该几何体可看作两个相同的四棱柱拼接而成,且四棱柱底面为直角梯形, 由题中数据可得,底面的上底为 3,下底为 6,高为 3,四棱柱的高为 3. 因此,该几何体的体积为 . 故选 C 【点睛】本题主要考查由几何体的三视图求几何体的体积问题,熟记棱柱的体积公式即可,属于常考题型. 10.已知数列 满足 ,数列 的前 项和为 ,则 ( ) A. B. C. D. 【答案】B 【解析】 【分析】 先由 求出 ,得到 ,再求出 ,即可求出结果. 【详解】因为 , 所以 , 12 (3 6) 3 3 542V = × × + × × = { }na 2 * 1 22 2 ... 2 ( )n na a a n n N+ + + = ∈ 2 2 1 1 log logn na a + n nS 1 2 3 10...S S S S⋅ ⋅ ⋅ ⋅ = 1 10 1 11 2 11 1 5 2 1 22 2 ... 2n na a a n+ + + = na 2 2 1 1 log logn na a + nS 2 1 22 2 ... 2n na a a n+ + + = 2 1 1 2 12 2 ... 2 1( 2)n na a a n n− −+ + + = − ≥ 两式作差,可得 ,即 , 又当 时, ,即 满足 ,因此 ; 所以 ; 因为数列 的前 项和为 , 所以 , 因此 . 故选 B 【点睛】本题主要考查数列的应用,根据递推公式求通项公式,由裂项相消法求数列的和,属于常考题型. 11.已知 是双曲线 的左、右焦点,若点 关于渐近线的对称点 也在双曲线 上,则该双曲线的离心率为( ) A. B. C. D. 【答案】D 【解析】 【分析】 根据双曲线的方程,先写出点 的坐标,以及其中一条渐近线方程,再求出点 坐标,代入双曲线方程, 即可得出结果. 【详解】因为双曲线方程为 ,所以其中一条渐近线方程为 , 又 是双曲线右焦点,记 ; 设点 关于渐近线 的对称点为 , 则有 ,解得 即 , 又点 在双曲线上, 2 1n na = 1 ( 2)2n na n= ≥ 1n = 12 1a = 1 1 2a = 1 2n na = *1 2 ( )2 n n na n N−= = ∈ 2 2 2 1 1 2 1 1 1 1 1 log log log l2 2og ( 1) 1n n n na a n n n n+ − − −= = = −+ + 2 2 1 1 log logn na a + n nS 1 1 1 1 1 1(1 ) ( ) ... ( ) 12 2 3 1 1 1n nS n n n n = − + − + + − = − =+ + + 1 2 3 10 1 2 3 10 1... ...2 3 4 11 11S S S S⋅ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ = 1 2,F F 2 2 2 2 1( 0, 0)x y a ba b − = > > 2F M 5 2 2 2 5 2F M 2 2 2 2 1( 0, 0)x y a ba b − = > > by xa = 2F 2 ( ,0)F c 2F by xa = ( , )M x y 2 2 y a x c b y b x c a = − − + = ⋅ 2bx c aby c = − = 2 22 2( , )a c abM c c − M 所以 ,整理得 , 所以离心率为 . 故选 D 【点睛】本题主要考查求双曲线的离心率,熟记双曲线的简单性质即可,属于常考题型. 12.定义在 上的函数 满足 , ,则关于 的不等式 的解集为( ) A. B. C. D. 【答案】A 【解析】 【分析】 先构造函数 ,对 求导,根据题中条件,得到 单调性,再由 求 出 ,将不等式 化为 ,即可求出结果. 【详解】令 ,则 , 因为 时, , 所以 , 即函数 在 上单调递增; 又 ,所以 ; 由 得 , 所以 , 2 22 2 2 2 2 2 1 a c ab c c a b − − = 2 25c a= 5ce a = = ∞(0,+ ) f x( ) 2 ( ) 1 0x f x′ + > 52 2f =( ) x 1 2lnf lnx x > +( ) 2( , )e +∞ 2(0, )e 2( , )e e 2(1, )e 1( ) ( ) ( 0)g x f x xx = − > ( )g x ( )g x 52 2f =( ) (2) 2g = 1 2lnf lnx x > +( ) (ln ) (2)g x g> 1( ) ( ) ( 0)g x f x xx = − > 2 2 2 1 ( ) 1( ) ( ) x f xg x f x x x ′ +′ ′= + = 0x > 2 ( ) 1 0x f x′ + > 2 2 2 1 ( ) 1( ) ( ) 0x f xg x f x x x ′ +′ ′= + = > 1( ) ( )g x f x x = − ∞(0,+ ) 52 2f =( ) 1(2) (2) 22g f= − = 1 2lnf lnx x > +( ) 1 2lnf lnx x − >( ) (ln ) (2)g x g> 因此, ,解得 . 故选 A 【点睛】本题主要考查导数的应用,构造函数,利用导数的方法研究函数单调性即可求解,属于常考题型. 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.若 满足约束条件 则 的最小值为__________. 【答案】2 【解析】 【分析】 先由约束条件作出可行域,再由目标函数 可化为 ,因此当直线 在 轴 上截距最小时, 取最小,结合图像即可求出结果. 【详解】由约束条件 作出可行域如下: 因为目标函数 可化为 , 因此当直线 在 轴上截距最小时, 取最小. 由图像易得,当直线 过点 时,在 轴上截距最小, 即 . 故答案为 2 【点睛】本题主要考查简单的线性规划,只需由约束条件作出可行域,分析目标函数的几何意义,结合图 ln 2x > 2x e> ,x y 4 0, 2 0, 2 0, x y x x y − + ≥ − ≤ + − ≥ 2z x y= + 2z x y= + 1 2 2 zy x= − + 1 2 2 zy x= − + y 2z x y= + 4 0, 2 0, 2 0, x y x x y − + ≥ − ≤ + − ≥ 2z x y= + 1 2 2 zy x= − + 1 2 2 zy x= − + y 2z x y= + 1 2 2 zy x= − + (2,0)A y min 2z = 像即可求解,属于常考题型. 14. 的展开式中各项系数之和为 81,则展开式中 的系数为_______. 【答案】24 【解析】 【分析】 先由题意求出 ,再由二项展开式的通项公式,即可求出结果. 【详解】因为 的展开式中各项系数之和为 81, 所以 ,解得 , 因此 的展开式的通项是 , 由 得 , 所以,展开式中 的系数为 . 故答案为 24 【点睛】本题主要考查求指定项的系数,熟记二项式定理即可,属于常考题型. 15.在边长为 的菱形 中, ,沿对角线 折起,使二面角 的大小为 , 这时点 在同一个球面上,则该球的表面积为____. 【答案】 【解析】 【分析】 取 的中点 ,连接 、 ,可知外接球的球心在面 中,再作 ,分别求出 与 的 长度后即可得解. 1(2 )nx x + x n 1(2 )nx x + (2 1) 81n+ = 4n = 41(2 )x x + 344 4 42 2 1 4 42 2 r r r r r r r rT C x x C x − −− − − + = = 34 12 r− = 2r = x 2 2 4 2 24C = 2 3 ABCD 60A °= BD A BD C− − 120° , , ,A B C D 28π BD E AE CE AEC OG CE⊥ OG CG 【详解】 如图 1,取 的中点 ,连接 、 ,由已知易知面 面 ,则外接球的球心在面 中.由 二面角 的大小为 可知 . 在面 中,设球心为 ,作 ,连接 , 易知 在面 上的投影即为 , 平分 , 为 的中心, , , , . 故答案为: 【点睛】本题考查了立体图形外接球体积的求解,考查了空间想象能力,属于中档题. 16.已知抛物线 的焦点为 , 为 轴正半轴上的一点.且 ( 为坐标原点),若抛 物线 上存在一点 ,其中 ,使过点 的切线 ,则切线 在 轴上的截距为_______. 【答案】-1 【解析】 【分析】 先对函数 求导,求出抛物线 在点 处的切线斜率,再根据 ,得到 点坐标, 由过点 的切线 ,求出 点坐标,进而可得切线方程,即可求出结果. 【详解】因为抛物线方程 可化为 ,所以 , 因此抛物线 在点 处的切线斜率为 ; 又 为抛物线 的焦点,所以 ; 因为 为 轴正半轴上的一点,且 ,所以 , BD E AE CE AEC ⊥ BCD AEC A BD C− − 120° 120AEC∠ = AEC O OG CE⊥ OE O BCD G OE AEC∠ ∴ G BCD∆ ∴ 2 2CG GE= = ∴ tan 60 3OG GE= ⋅ = ∴ 2 2 7OC GC GO= + = ∴ ( )2 =4 7 =28S π π×球 28π 2: 4C x y= F E y 3OE OF= O C 0 0( , )M x y 0 0x ≠ M l ME⊥ l y 21 4y x= C 0 0( , )M x y 3OE OF= E M l ME⊥ M 2 4x y= 21 4y x= 1 2y x′ = C 0 0( , )M x y 0 1 2k x= F 2: 4C x y= (0,1)F E y 3OE OF= (0,3)E 所以 , 因为过点 的切线 ,所以 ,解得 , 因为 在抛物线上,所以 ,因此 ; 所以切线方程为 或 ,即 , 因此切线 在 轴上的截距为 【点睛】本题主要考查直线与抛物线位置关系,熟记抛物线的性质即可,属于常考题型. 三、解答题(本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤) 17.在 中,角 , , 的对边分别是 , , .已知 . (Ⅰ)求角 的值; (Ⅱ)若 , ,求 面积. 【答案】(I) ;(II) 【解析】 【分析】 (Ⅰ)由 ,利用正弦定理以及两角和与差的正弦公式可得 ,结 合角 的范围可得结果;(Ⅱ)由余弦定理可得 ,求出 的值,利用三角形面积公式可得 结果. 【详解】(Ⅰ)∵ , ∴由正弦定理可得, , 因为 , ∴ ,∴ . 的 0 0 3 ME yk x −= M l ME⊥ 0 0 0 31 12ME yk k x x −⋅ = ⋅ = − 0 1y = 0 0( , )M x y 0 2x = ± 0 1 12k x= = ± 1 2y x− = − 1 ( 2)y x− = − + 1y x= ± − l y 1− ABC∆ A B C a b c sin sin 03b C c B π − − = C 4a = 2 7c = ABC∆ 2 3C π= 2 3S = sin sin 03b C c B π − − = sin 03C π + = C 2 4 12 0b b+ − = b sin sin 03b C c B π − − = 1 3sin sin cos sin sin 02 2B C C C B − − = sin 0B ≠ 1 3sin cos 02 2C C+ = sin 03C π + = ∵ ,∴ . (Ⅱ)∵ ,∴ , ∵ ,∴ , ∴ . 【点睛】本题主要考查正弦定理、余弦定理及两角和与差的正弦公式,属于中档题.对余弦定理一定要熟记 两种形式:(1) ;(2) ,同时还要熟练掌握运用两种形式 的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住 等特殊角的三角函数值, 以便在解题中直接应用. 18.某商场营销人员进行某商品的市场营销调查时发现,每回馈消费者一定的点数,该商品每天的销量就会 发生一定的变化,经过试点统计得到以下表: 反馈点数 t 1 2 3 4 5 销量(百件)/天 0.5 0.6 1 1.4 1.7 (Ⅰ)经分析发现,可用线性回归模型 拟合当地该商品销量 (千件)与返还点数 之间 相 关关系.试预测若返回 6 个点时该商品每天的销量; (Ⅱ)若节日期间营销部对商品进行新一轮调整.已知某地拟购买该商品 消费群体十分庞大,经营销调研 机构对其中的 200 名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表: 返还点数预期值区间 (百分比) [1,3) [3,5) [5,7) [7,9) [9,11) [11,13) 频数 20 60 60 30 20 10 (1)求这 200 位拟购买该商品的消费者对返点点数的心理预期值 的样本平均数及中位数的估计值(同一 区间的预期值可用该区间的中点值代替;估计值精确到 0.1); (2)将对返点点数的心理预期值在 和 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨 的 的 ( )0,C π∈ 2 3C π= 2 2 2 2 cosc a b ab C= + − 2 4 12 0b b+ − = 0b > 2b = 1 1 3sin 2 4 2 32 2 2S ab C= = × × × = 2 2 2 2 cosa b c bc A= + − 2 2 2 cos 2 b c aA bc + −= 30 ,45 ,60o o o 0.08y bt= + y t x [1,3) [11,13] 胀型”消费者,现采用分层抽样的方法从位于这两个区间的 30 名消费者中随机抽取 6 名,再从这 6 人中随 机抽取 3 名进行跟踪调查,设抽出的 3 人中 “欲望紧缩型”消费者的人数为随机变量 ,求 的分布列 及数学期望. 【答案】(Ⅰ)返回 6 个点时该商品每天销量约为 2 百件;(Ⅱ)(1)均值 的估计值为 6, 中位数的估计 值为 5.7;(2)详见解析. 【解析】 【分析】 (Ⅰ)先由题中数据得到 ,根据回归直线必过样本中心,将 代入 ,即可求出结果; (Ⅱ)(1)根据频数表中数据,每组的中间值乘以该组的频率,再求和,即可得出平均值;根据中位数两 侧的频率之和均为 0.5,即可求出结果; (2)先求出抽取 6 名消费者中“欲望紧缩型”消费者人数与“欲望膨胀型”消费者人数,根据题意得到 的可能取值,求出其对应概率,即可得出分布列与数学期望. 【详解】解:(Ⅰ)由题意可得: , 因为线性回归模型为 ,所以 ,解得 ; 故 关于 的线性回归方程为 , 当 时, ,即返回 6 个点时该商品每天销量约为 2 百件. (Ⅱ)(1)根据题意,这 200 位拟购买该商品的消费者对返回点数的心里预期值 的平均值 的估计值为: , 中位数的估计值为 . (2)抽取 6 名消费者中“欲望紧缩型”消费者人数为 , “欲望膨胀型”消费者人数为 . 由题意 的可能取值为 , 所以 , , 故随机变量 的分布列为 X 1 2 3 X X x ,t y ,t y 0.08y bt= + X 1 2 3 4 5 0.5 0.6 1 1.4 1.73, 1.045 5t y + + + + + + + += = = = 0.08y bt= + 1.04 3 0.08b= + 0.32b = y t 0.32 0.08y t= + 6t = 2.00y = X x 2 0.1 4 0.3 6 0.3 8 0.15 10 0.1 12 0.05 6x = × + × + × + × + × + × = 100 20 60 25 2 5 5.760 3 − −+ × = + ≈ 206 430 × = 106 230 × = X 1,2,3 1 2 4 2 3 6 1( 1) 5 C CP X C = = = 2 1 4 2 3 6 3( 2) 5 C CP X C = = = 3 0 4 2 3 6 1( 3) 5 C CP X C = = = X P . 【点睛】本题主要考查线性回归分析、考查根据频数表求平均值与中位数、以及超几何分布,熟记线性回 归分析的基本思想,以及平均数、中位数的计算方法、超几何分布的概念等即可,属于常考题型. 19.如图,在直三棱柱 中,平面 侧面 ,且 , (Ⅰ)求证: ; (Ⅱ)若直线 与平面 所成角的大小为 ,求锐二面角 的大小. 【答案】(Ⅰ)详见解析;(Ⅱ) . 【解析】 【分析】 (Ⅰ)先取 的中点 ,连接 ,根据线面垂直的判定定理,证明 侧面 ,进而可得出 ; (Ⅱ)根据(Ⅰ)的结果,得到 且 底面 ,以点 为原点,以 所在直线 分别为 , , 轴建立空间直角坐标系 ,设 ,表示出 ,再求出平面 的一个法 向量,根据直线 与平面 所成角的大小为 ,求出 ,再求出平面 的一个法向量,由向量 夹角公式,即可求出结果. 【详解】(Ⅰ)如图,取 的中点 ,连接 . 1 5 3 5 1 5 1 3 1( ) 1 2 3 25 5 5E X = × + × + × = 1 1 1ABC A B C− 1A BC ⊥ 1 1ABB A 1 2AA AB= = AB BC⊥ AC 1A BC 30 1A AC B− − 60 1A B D AD BC ⊥ 1 1ABB A AB BC⊥ AB BC⊥ 1BB ⊥ ABC B 1BC BA BB、 、 x y z B xyz− BC a= AC 1A BC AC 1A BC 30 a 1A AC 1A B D AD 因为 ,所以 . 由平面 侧面 ,且平面 侧面 , 得 平面 . 又 平面 ,所以 , 因为三棱柱 是直三棱柱,则 底面 ,所以 又 ,从而 侧面 , 又 侧面 ,故 . (Ⅱ)由(1)知 且 底面 ,所以以点 为原点,以 所在直线分别为 , , 轴建立空间直角坐标系 . 设 ,则 , , , , , , , . 设平面 的一个法向量 ,由 , ,得 . 令 ,得 ,则 . 设直线 与平面 所成的角为 ,则 , 所以 , 解得 , 即 . 又设平面 的一个法向量为 ,同理可得 . 设锐二面角 的大小为 ,则 , 由 ,得 . ∴锐二面角 的大小为 . 1AA AB= 1AD A B⊥ 1A BC ⊥ 1 1A ABB 1A BC 1 1 1A ABB A B= AD ⊥ 1A BC BC ⊂ 1A BC AD BC⊥ 1 1 1ABC A B C− 1AA ⊥ ABC 1AA BC⊥ 1AA AD A= BC ⊥ 1 1ABB A AB Ì 1 1A ABB AB BC⊥ AB BC⊥ 1BB ⊥ ABC B 1BC BA BB、 、 x y z B xyz− BC a= ( )0,2,0A ( )0,0,0B ( ),0,0C a 1(0,2,2)A ( ,0,0)BC a= 1 (0,2,2)BA = ( , 2,0)AC a= − 1 (0,0,2)AA = 1A BC ( )1 , ,n x y z= 1BC n⊥ 1 1BA n⊥ 0 2 2 0 xa y z = + = 1y = 0, 1x z= = − ( )1 0,1, 1n = − AC 1A BC θ 30θ = 1 2 1 2 1sin30 24 2 AC n AC n a ⋅ = = = + 2a = (2, 2,0)AC = − 1A AC 2n 2 (1,1,0)n = 1A AC B− − α 1 2 1 2 1 2 1cos cos , 2 n nn n n n α ⋅= = = 0, 2 πα ∈ 60α = 1A AC B− − 60 【点睛】本题主要考查证明线线垂直、以及已知线面角求其它量和求二面角的问题,熟记线面垂直的判定 定理与性质定理,灵活运用向量的方法求空间角即可,属于常考题型. 20.椭圆 的左、右焦点分别为 ,离心率为 ,过焦点 且垂直于 轴的 直线被椭圆 截得的线段长为 . (Ⅰ)求椭圆 的方程; (Ⅱ)点 为椭圆 上一动点,连接 、 ,设 的角平分线 交椭圆 的 长轴于点 ,求实数 的取值范围. 【答案】(Ⅰ) ;(Ⅱ) . 【解析】 【分析】 (Ⅰ)先将 代入 ,得到弦长为 ,根据题中条件,列出方程组,求解即可得到 , 进而可求出椭圆方程; (Ⅱ)先设点 ,根据题意,得到直线 的方程,再由 的角平分线 交 椭圆 的长轴于点 ,得到 到直线 的相等,进而得出 ,根据 范围,即 可求出结果. 【详解】(Ⅰ)将 代入 中,由 可得 , 所以弦长为 , 2 2 2 2: 1( 0)x yC a ba b + = > > 1 2,F F 3 2 2F x C 1 C 0 0 0( , )( 0)P y yx ≠ C 1PF 2PF 1 2F PF∠ PM C ( ,0)M m m 2 2 14 x y+ = 3 3 2 2 − <查看更多