2013北京卷（文）数学试题

2013北京卷（文）数学试题

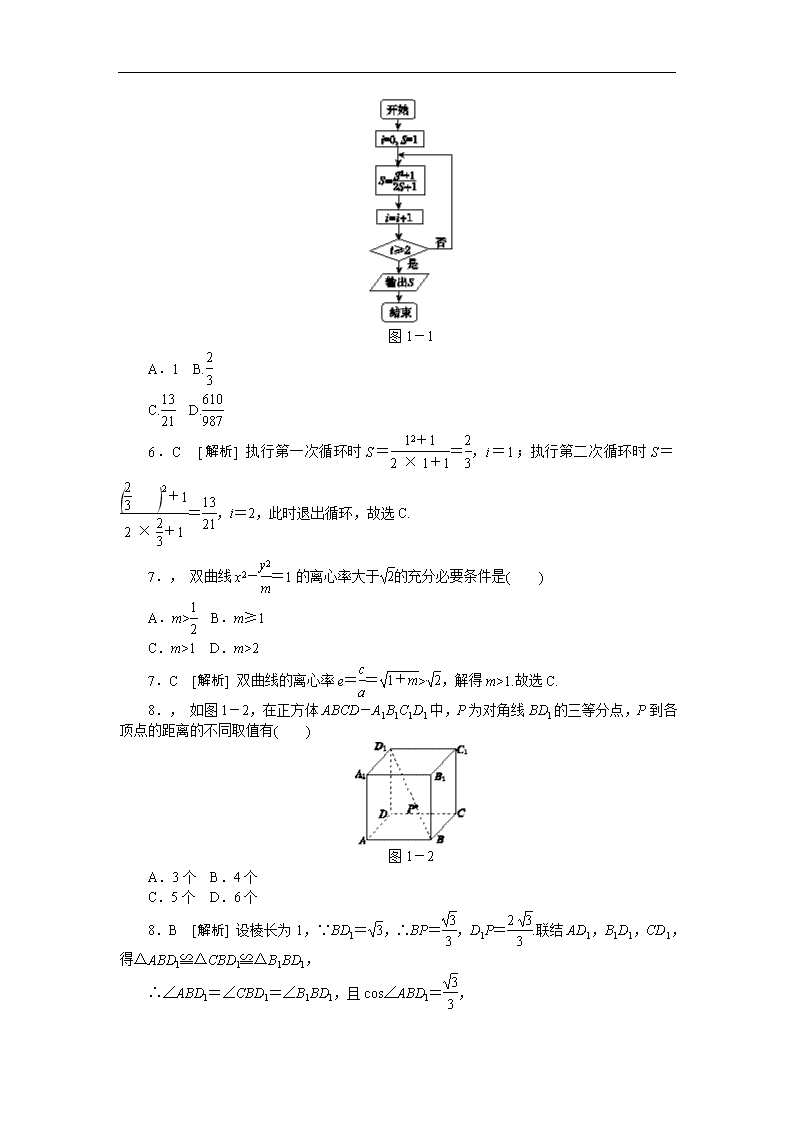
‎2013·北京卷(文科数学)‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1． 已知集合A＝{－1，0，1}，B＝{x|－1≤x<1}，则A∩B＝(　　)‎ A．{0} B．{－1，0} ‎ C．{0，1} D．{－1，0，1}‎ ‎1．B　[解析] ∵－1∈B，0∈B，1∉B，∴A∩B＝{－1，0}，故选B.‎ ‎2． 设a，b，c∈，且a>b，则(　　)‎ A．ac>bc B.< C．a2>b2 D．a3>b3‎ ‎2．D　[解析] ∵函数y＝x3在上是增函数，a>b，‎ ‎∴a3>b3.‎ ‎3．， 下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是(　　)‎ A．y＝ B．y＝e－x C．y＝－x2＋1 D．y＝lg |x|‎ ‎3．C　[解析] 对于A，y＝是奇函数，排除．对于B，y＝e－x既不是奇函数，也不是偶函数，排除．对于D，y＝lg |x|是偶函数，但在(0，＋∞)上有y＝lgx，此时单调递增，排除．只有C符合题意．‎ ‎4． 在复平面内，复数i(2－i)对应的点位于(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．A　[解析] ∵i(2－i)＝2i＋1，∴i(2－i)对应的点为(1，2)，因此在第一象限．‎ ‎5． 在△ABC中，a＝3，b＝5，sin A＝，则sin B＝(　　)‎ A. B. C. D．1‎ ‎5．B　[解析] 由正弦定理得＝，即＝，解得sin B＝.‎ ‎6． 执行如图1－1所示的程序框图，输出的S值为(　　)‎ 图1－1‎ A．1 B. C. D. ‎6．C　[解析] 执行第一次循环时S＝＝，i＝1；执行第二次循环时S＝＝，i＝2，此时退出循环，故选C.‎ ‎7．， 双曲线x2－＝1的离心率大于的充分必要条件是(　　)‎ A．m> B．m≥1‎ C．m>1 D．m>2‎ ‎7．C　[解析] 双曲线的离心率e＝＝>，解得m>1.故选C.‎ ‎8．， 如图1－2，在正方体ABCD－A1B1C1D1中，P为对角线BD1的三等分点，P到各顶点的距离的不同取值有(　　)‎ 图1－2‎ A．3个 B．4个 C．5个 D．6个 ‎8．B　[解析] 设棱长为1，∵BD1＝，∴BP＝，D1P＝.联结AD1，B1D1，CD1，得△ABD1≌△CBD1≌△B1BD1，‎ ‎∴∠ABD1＝∠CBD1＝∠B1BD1，且cos∠ABD1＝，‎ 联结AP，PC，PB1，则有△ABP≌△CBP≌△B1BP，‎ ‎∴AP＝CP＝B1P＝，同理DP＝A1P＝C1P＝1，‎ ‎∴P到各顶点的距离的不同取值有4个．‎ ‎9． 若抛物线y2＝2px的焦点坐标为(1，0)，则p＝________；准线方程为________. ‎ ‎9．2　x＝－1　[解析] ∵抛物线y2＝2px的焦点坐标为(1，0)，∴＝1，解得p＝2，∴准线方程为x＝－1.‎ ‎10．， 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．‎ 图1－3‎ ‎10．3　[解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V＝×(3×3)×1＝3.‎ ‎11． 若等比数列{an}满足a2＋a4＝20，a3＋a5＝40，则公比q＝________；前n项和Sn＝________．‎ ‎11．2　2n＋1－2　[解析] ∵a3＋a5＝q(a2＋a4)，∴40＝20q，∴q＝2，∴a1(q＋q3)＝20，∴a1＝2，∴Sn＝＝2n＋1－2.‎ ‎12． 设D为不等式组表示的平面区域，区域D上的点与点(1，0)之间的距离的最小值为________．‎ ‎12.‎ 　[解析] 在平面直角坐标系中画出可行域，如图所示．根据可行域可知，区域D内的点到点(1，0)的距离最小值为点(1，0)到直线2x－y＝0的距离，即d＝＝.‎ ‎13． 函数f(x)＝的值域为________．‎ ‎13．(－∞，2)　[解析] 函数y＝logx在(0，＋∞)上为减函数，当x≥1时，函数y＝logx的值域为(－∞，0]；函数y＝2x在上是增函数，当x<1时，函数y＝2x的值域为(0，2)，所以原函数的值域为(－∞，2)．‎ ‎14． 已知点A(1，－1)，B(3，0)，C(2，1)．若平面区域D由所有满足＝λ＋μ(1≤λ≤2，0≤μ≤1)的点P组成，则D的面积为________．‎ ‎14．3　[解析] 设P(x，y)，∴＝(x－1，y＋1)，＝(2，1)，＝(1，2)．∵＝λ＋μ，‎ ‎∴解得 又1≤λ≤2，0≤μ≤1，∴此不等式组表示的可行域为平行四边形，如图所示，‎ 由于A(3，0)，B(5，1)，所以|AB|＝＝，点B(5，1)到直线x－2y＝0的距离d＝，∴其面积S＝×＝3.‎ ‎15．，，， 已知函数f(x)＝(2cos2x－1)sin 2x＋cos 4x.‎ ‎(1)求f(x)的最小正周期及最大值；‎ ‎(2)若α∈，且f(α)＝，求α的值．‎ ‎15．解：(1)因为f(x)＝(2cos2 x－1)sin 2x＋cos 4x ‎＝cos 2x·sin 2x＋cos 4x ‎＝(sin 4x＋cos 4x)‎ ‎＝sin，‎ 所以f(x)的最小正周期为，最大值为.‎ ‎(2)因为f(α)＝，所以sin＝1.‎ 因为α∈，所以4α＋∈.‎ 所以4α＋＝.故α＝.‎ ‎16．，， 图1－4是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天．‎ 图1－4‎ ‎(1)求此人到达当日空气质量优良的概率；‎ ‎(2)求此人在该市停留期间只有1天空气重度污染的概率；‎ ‎(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)‎ ‎16．解：(1)在3 月1日至3 月13日这13天中，1日、2日、3日、7日、12日、13日共6天的空气质量优良，所以此人到达当日空气质量优良的概率是.‎ ‎(2)根据题意，事件“此人在该市停留期间只有1天空气 重度污染”等价于“此人到达该市的日期是4日，或5日，或7日，或8日”．‎ 所以此人在该市停留期间只有1天空气重度污染的概率为.‎ ‎(3)从3月5日开始连续三天的空气质量指数方差最大．‎ ‎17．，， 如图1－5，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：‎ ‎(1)PA⊥底面ABCD；‎ ‎(2)BE∥平面PAD；‎ ‎(3)平面BEF⊥平面PCD.‎ 图1－5‎ ‎17．证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.‎ ‎(2)因为AB∥CD，CD＝2AB，E为CD的中点，‎ 所以AB∥DE，且AB＝DE，‎ 所以ABED为平行四边形，‎ 所以BE∥AD.‎ 又因为BE⊄平面PAD，AD⊂平面PAD，‎ 所以BE∥平面PAD.‎ ‎(3)因为AB⊥AD，而且ABED为平行四边形，‎ 所以BE⊥CD，AD⊥CD.‎ 由(1)知PA⊥底面ABCD，‎ 所以PA⊥CD.‎ 又因为AD∩PA＝A，所以CD⊥平面PAD，‎ 所以CD⊥PD.‎ 因为E和F分别是CD和PC的中点，‎ 所以PD∥EF，‎ 所以CD⊥EF，‎ 所以CD⊥平面BEF，‎ 所以平面BEF⊥平面PCD.‎ ‎18．，，， 已知函数f(x)＝x2＋xsin x＋cos x.‎ ‎(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值；‎ ‎(2)若曲线y＝f(x)与直线y＝b有两个不同交点，求b的取值范围．‎ ‎18．解：由f(x)＝x2＋xsin x＋cos x，得 f′(x)＝x(2＋cos x)．‎ ‎(1)因为曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，所以f′(a)＝a(2＋cos a)＝0，b＝f(a)．‎ 解得a＝0，b＝f(0)＝1.‎ ‎(2)令f ′(x)＝0，得x＝0.‎ f(x)与f′(x)的情况如下：‎ x ‎(－∞，0)‎ ‎0‎ ‎(0，＋∞)‎ f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎  ‎1‎  所以函数f(x)在区间(－∞，0)上单调递减，在区间(0，＋∞)上单调递增，f(0)＝1是f(x)的最小值．‎ 当b≤1时，曲线y＝f(x)与直线y＝b最多只有一个交点；‎ 当b>1时，f(－2b)＝f(2b)≥4b2－2b－1>4b－2b－1>b，f(0)＝11时，曲线y＝f(x)与直线y＝b有且仅有两个不同交点．‎ 综上可知，如果曲线y＝f(x)与直线y＝b有两个不同交点，那么b的取值范围是(1，＋∞)．‎ ‎19．，， 直线y＝kx＋m(m≠0)与椭圆W：＋y2＝1相交于A，C两点，O是坐标原点．‎ ‎(1)当点B的坐标为(0，1)，且四边形OABC为菱形时，求AC的长；‎ ‎(2)当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形．‎ ‎19．解：(1)因为四边形OABC为菱形，所以AC与OB相互垂直平分．‎ ‎ 所以可设A，代入椭圆方程得＋＝1，即t＝±.‎ 所以|AC|＝2 .‎ ‎(2)证明：假设四边形OABC为菱形．‎ 因为点B不是W的顶点，且AC⊥OB，所以k≠0.‎ 由消y并整理得 ‎(1＋4k2)x2＋8kmx＋4m2－4＝0.‎ 设A(x1，y1)，C(x2，y2)，则 ＝－，＝k·＋m＝.‎ 所以AC的中点为M.‎ 因为M为AC和OB的交点，且m≠0，k≠0，所以直线OB的斜率为－.‎ 因为k·≠－1，所以AC与OB不垂直．‎ 所以OABC不是菱形，与假设矛盾．‎ 所以当点B不是W的顶点时，四边形OABC不可能是菱形．‎ ‎20．，，， 给定数列a1，a2，…，an，对i＝1，2，…，n－1，该数列前i项的最大值记为Ai，后n－i项ai＋1，ai＋2，…，an的最小值记为Bi，di＝Ai－Bi.‎ ‎(1)设数列{an}为3，4，7，1，写出d1，d2，d3的值；‎ ‎(2)设a1，a2，…，an(n≥4)是公比大于1的等比数列，且a1>0.证明：d1，d2，…，dn－1是等比数列；‎ ‎(3)设d1，d2，…，dn－1是公差大于0的等差数列，且d1>0，证明：a1，a2，…，an－1是等差数列．‎ ‎20．解：(1)d1＝2，d2＝3，d3＝6.‎ ‎(2)证明：因为a1>0，公比q>1，‎ 所以a1，a2，…，an是递增数列．‎ 因此，对i＝1，2，…，n－1，Ai＝ai，Bi＝ai＋1.‎ 于是对i＝1，2，…，n－1，‎ di＝Ai－Bi＝ai－ai＋1＝a1(1－q)qi－1.‎ 因此di≠0且＝q(i＝1，2，…，n－2)，‎ 即d1，d2，…，dn－1是等比数列．‎ ‎(3)证明：设d为d1，d2，…，dn－1的公差．‎ 对1≤i≤n－2，因为Bi≤Bi＋1，d>0，所以Ai＋1＝Bi＋1＋di＋1≥Bi＋di＋d>Bi＋di＝Ai.‎ 又因为Ai＋1＝max{Ai，ai＋1}，所以ai＋1＝Ai＋1>Ai≥ai.‎ 从而a1，a2，…，an－1是递增数列，因此Ai＝ai(i＝1，2，…，n－1)．‎ 又因为B1＝A1－d1＝a1－d1

查看更多