人教版高三数学总复习课时作业52

人教版高三数学总复习课时作业52

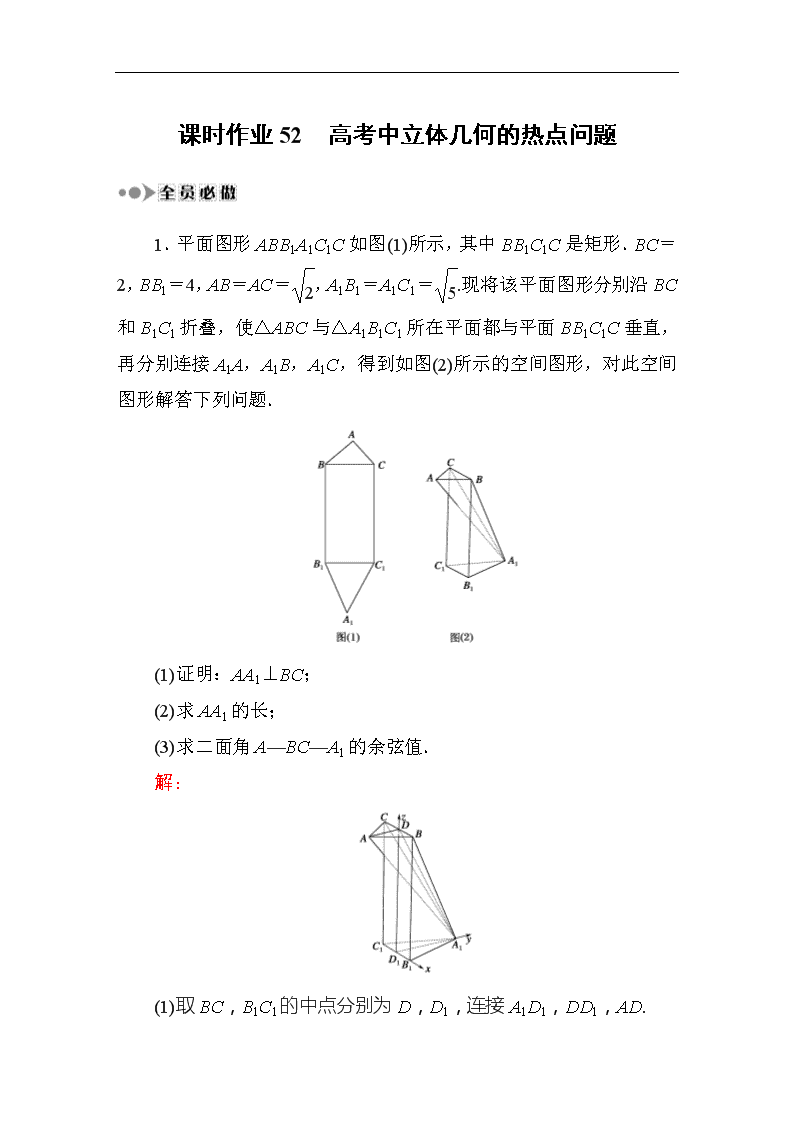
课时作业52　高考中立体几何的热点问题 ‎1．平面图形ABB1A1C1C如图(1)所示，其中BB1C1C是矩形．BC＝2，BB1＝4，AB＝AC＝，A1B1＝A1C1＝.现将该平面图形分别沿BC和B1C1折叠，使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直，再分别连接A1A，A1B，A1C，得到如图(2)所示的空间图形，对此空间图形解答下列问题．‎ ‎(1)证明：AA1⊥BC；‎ ‎(2)求AA1的长；‎ ‎(3)求二面角A—BC—A1的余弦值．‎ 解：‎ ‎(1)取BC，B1C1的中点分别为D，D1，连接A1D1，DD1，AD.‎ 由四边形BB1C1C为矩形，知DD1⊥B1C1.‎ 因为平面BB1C1C⊥平面A1B1C1，‎ 所以DD1⊥平面A1B1C1.‎ 由A1B1＝A1C1，知A1D1⊥B1C1.‎ 故以D1为坐标原点，可建立如图所示的空间直角坐标系D1—xyz.‎ 由题设可得A1D1＝2，AD＝1.‎ 由以上可知AD⊥平面BB1C1C，A1D1⊥平面BB1C1C，于是AD∥A1D1.‎ 所以A(0，－1,4)，B(1,0,4)，A1(0,2,0)，C(－1,0,4)，D(0,0,4)．‎ 故＝(0,3，－4)，＝(－2,0,0)，‎ 因为·＝0，所以⊥，即AA1⊥BC.‎ ‎(2)因为＝(0,3，－4)，所以||＝5，即AA1＝5.‎ ‎(3)连接A1D.‎ 由BC⊥AD，BC⊥AA1，可知BC⊥面A1AD，BC⊥A1D，‎ 所以∠ADA1为二面角A—BC—A1的平面角．‎ 因为＝(0，－1,0)，＝(0,2，－4)，‎ 所以cos〈，〉＝＝－，‎ 即二面角A—BC—A1的余弦值为－.‎ ‎2．在如图所示的几何体中，底面ABCD为菱形，∠BAD＝60°，AA1綊DD1綊CC1∥BE，且AA1＝AB，D1E⊥平面D1AC，AA1⊥底面ABCD.‎ ‎(1)求二面角D1—AC—E的大小；‎ ‎(2)在D1E上是否存在一点P，使得A1P∥平面EAC，若存在，求的值，若不存在，说明理由．‎ 解：‎ ‎(1)设AC与BD交于O，如图所示建立空间直角坐标系O－xyz，设AB＝2，则A(，0,0)，B(0，－1,0)，C(－，0,0)，D(0,1,0)，D1(0,1,2)，‎ 设E(0，－1，t)，t>0，则＝(0,2,2－t)，＝(2，0,0)，＝(，－1，－2)．‎ ‎∵D1E⊥面D1AC，∴D1E⊥CA，D1E⊥D1A，‎ ‎∴解得t＝3，∴E(0，－1,3)，‎ ‎∴＝(－，－1,3)，‎ 设平面EAC的法向量为m＝(x，y，z)，‎ 则∴ 令z＝1，y＝3，m＝(0,3,1)．‎ 又平面D1AC的法向量＝(0,2，－1)，‎ ‎∴cos〈m，〉＝＝.‎ 所以所求二面角的大小为45°.‎ ‎(2)假设存在点P满足题意．‎ 设＝λ＝λ(－)，‎ 得＝＝(0，－，)，‎ ＝＋＝(－，1,0)＋(0，－，)‎ ‎＝(－，1－，)‎ ‎∵A1P∥平面EAC，∴⊥m，‎ ‎∴－×0＋3×(1－)＋1×＝0，解得λ＝，‎ 故存在点P使A1P∥面EAC，此时D1PPE＝32.‎ ‎3．如图，在四棱锥P—ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且AD＝PA＝PD.‎ ‎(1)求证：平面PAB⊥平面PCD；‎ ‎(2)在线段AB上是否存在点G，使得平面PCD与平面PDG夹角的余弦值为？若存在，请说明理由．‎ 解：(1)∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，四边形ABCD为正方形，CD⊥AD，CD⊂平面ABCD，∴CD⊥平面PAD，∴CD⊥PA.‎ 又AD＝PA＝PD，∴△PAD为等腰直角三角形，‎ 且∠APD＝，即PA⊥PD.‎ 又CD∩PD＝D，且CD，PD⊂平面PDC，‎ ‎∴PA⊥平面PDC，‎ 又PA⊂平面PAB，∴平面PAB⊥平面PCD.‎ ‎(2)如图，取AD的中点O，连接OP.‎ ‎∵PA＝PD，∴PO⊥AD.‎ ‎∵侧面PAD⊥底面ABCD，‎ 平面PAD∩平面ABCD＝AD，‎ ‎∴PO⊥平面ABCD，‎ ‎∵AD＝PA＝PD，‎ ‎∴PA⊥PD，OP＝OA＝1.‎ 以O为原点，直线OA，OP分别为x，z轴，且底面ABCD中过O点垂直于AD的直线为y轴建立空间直角坐标系，则A(1,0,0)，D(－1,0,0)，P(0,0,1)．‎ 假设在AB上存在点G使得平面PCD与平面PDG夹角的余弦值为，连接PG，DG.‎ 设G(1，a,0)(0≤a≤2)．‎ 由(1)知平面PCD的一个法向量为＝(1,0，－1)．‎ 设平面PDG的法向量为n＝(x，y，z)．‎ ‎∵＝(1,0,1)，＝(－2，－a,0)，‎ ‎∴由n·＝0，n·＝0可得，‎ 令x＝1，则y＝－，z＝－1，故n＝(1，－，－1)，‎ ‎∴cos〈n，〉＝＝＝＝，解得，a＝.‎ ‎∴在线段AB上存在点G(1，，0)，‎ 使得平面PCD与平面PDG夹角的余弦值为.‎ ‎1．(2014·安徽卷)如右图，四棱柱ABCD ‎—A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD＝2BC.过A1，C，D三点的平面记为α，BB1与α的交点为Q.‎ ‎(1)证明：Q为BB1的中点；‎ ‎(2)求此四棱柱被平面α所分成上下两部分的体积之比；‎ ‎(3)若A1A＝4，CD＝2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小．‎ 解：(1)因为BQ∥AA1，BC∥AD，BC∩BQ＝B，AD∩AA1＝A.‎ 所以平面QBC∥平面A1AD.‎ 从而平面A1CD与这两个平面的交线相互平行，即QC∥A1D.‎ 故△QBC与△A1AD的对应边相互平行，于是△QBC∽△A1AD.‎ 所以＝＝＝，即Q为BB1的中点．‎ ‎(2)如图1，连接QA，QD.设AA1＝h，梯形ABCD的高为d，四棱柱被平面α所分成上下两部分的体积分别为V上和V下，BC＝a，则AD＝2a.‎ 图1‎ VQ—A1AD＝··2a·h·d＝ahd，‎ VQ—ABCD＝··d·(h)＝ahd，‎ 所以V下＝VQ—A1AD＋VQ—ABCD＝ahd，‎ 又VA1B1C1D1—ABCD＝ahd，‎ 所以V上＝VA1B1C1D1—ABCD－V下＝ahd－ahd＝ahd，故＝.‎ ‎(3)解法1：如图1，在△ADC中，作AE⊥DC，垂足为E，连接A1E.‎ 又DE⊥AA1，且AA1∩AE＝A，‎ 所以DE⊥平面AEA1，于是DE⊥A1E.‎ 所以∠AEA1为平面α与底面ABCD所成二面角的平面角．‎ 因为BC∥AD，AD＝2BC，所以S△ADC＝2S△BCA.‎ 因为梯形ABCD的面积为6，DC＝2，所以S△ADC＝4，AE＝4.‎ 于是tan∠AEA1＝＝1，∠AEA1＝.‎ 故平面α与底面ABCD所成二面角的大小为.‎ 图2‎ 解法2：如图2，以D为原点，，分别为x轴和z轴正方向建立空间直角坐标系．‎ 设∠CDA＝θ.‎ 因为SABCD＝·2sinθ＝6，‎ 所以a＝.从而C(2cosθ，2sinθ，0)，A1(，0,4)，‎ 所以＝(2cosθ，2sinθ，0)，＝(，0,4)．‎ 设平面A1DC的法向量为n＝(x，y,1)，‎ 由得x＝－sinθ，y＝cosθ，‎ 所以n＝(－sinθ，cosθ，1)．‎ 因为平面ABCD的法向量为m＝(0,0,1)，‎ 所以cos〈n，m〉＝＝，‎ 故平面α与底面ABCD所成二面角的大小为.‎ ‎2．如图，在四棱锥S—ABCD中，底面ABCD是直角梯形，侧棱SA⊥底面ABCD，AB垂直于AD和BC，SA＝AB＝BC＝2，AD＝1.M是棱SB的中点．‎ ‎(1)求证：AM∥平面SCD；‎ ‎(2)求平面SCD与平面SAB所成二面角的余弦值；‎ ‎(3)设点N是直线CD上的动点，MN与平面SAB所成的角为θ，求sinθ的最大值．‎ 解：‎ ‎(1)证明：以点A为原点建立如图所示的空间直角坐标系，则 A(0,0,0)，B(0,2,0)，C(2,2,0)，D(1,0,0)，S(0,0,2)，M(0,1,1)．‎ 则＝(0,1,1)，＝(1,0，－2)，＝(－1，－2,0)．‎ 设平面SCD的法向量是n＝(x，y，z)，‎ 则即 令z＝1，则x＝2，y＝－1，于是n＝(2，－1,1)．‎ ‎∵·n＝0，∴⊥n.又AM⊄平面SCD，‎ ‎∴AM∥平面SCD.‎ ‎(2)易知平面SAB的一个法向量为n1＝(1,0,0)．设平面SCD与平面SAB所成的二面角为φ，‎ 则|cosφ|＝＝ ‎＝＝，即cosφ＝.‎ ‎∴平面SCD与平面SAB所成二面角的余弦值为.‎ ‎(3)设N(x,2x－2,0)(x∈[1,2])，则＝(x,2x－3，－1)．‎ 又平面SAB的一个法向量为n1＝(1,0,0)，‎ ‎∴sinθ＝ ‎＝＝ ‎＝＝.‎ 当＝，即x＝时，(sinθ)max＝.‎