2013届人教A版文科数学课时试题及解析(5)函数的单调性与最值
课时作业(五) [第5讲 函数的单调性与最值]
[时间:45分钟 分值:100分]
1. 下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
A.y=x3 B.y=|x|+1
C.y=-x2+1 D.y=2-|x|
2.已知函数f(x)为R上的减函数,则满足f
0恒成立,则实数m的取值范围是( )
A.(0,1) B.(-∞,0)
C. D.(-∞,1)
9. 已知函数f(x)=若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(1,2010) B.(1,2011)
C.(2,2011) D.[2,2011]
10. 已知f(x)=是(-∞,+∞)上的减函数,那么a的取值范围是________.
11.对a,b∈R,记max(a,b)=函数f(x)=max(|x+1|,|x-2|)(x∈R)的最小值是________.
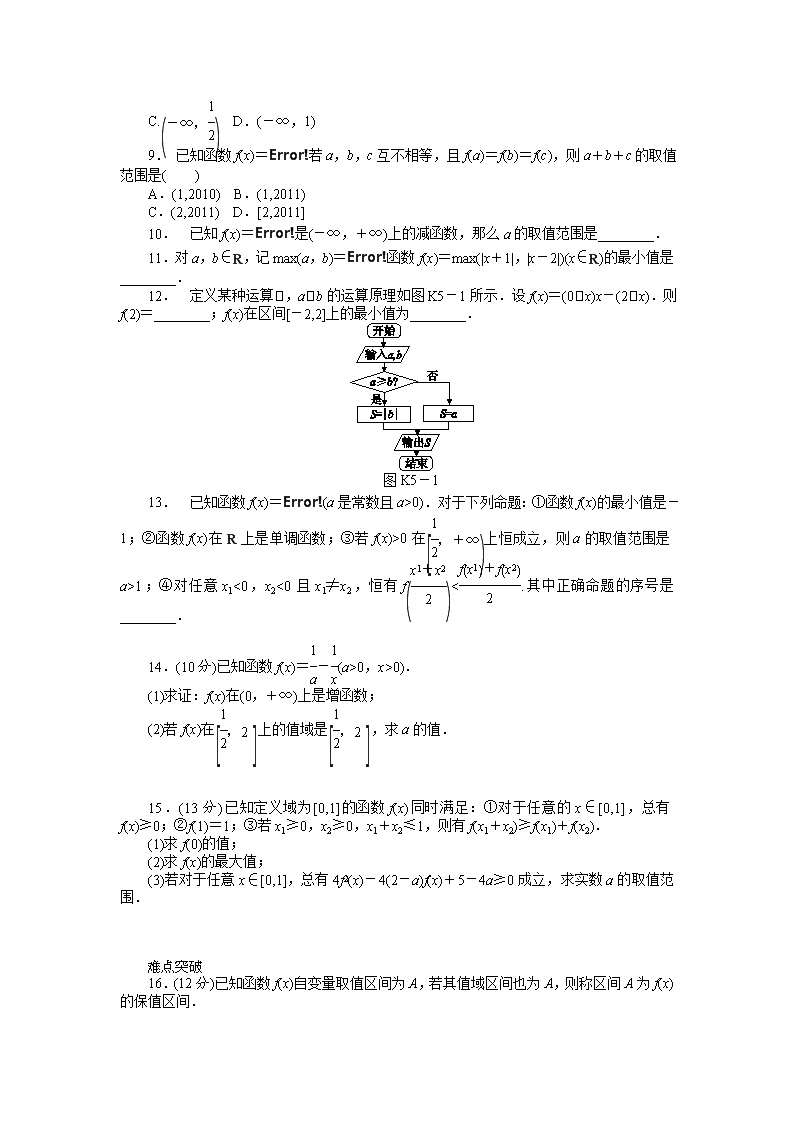
12. 定义某种运算,ab的运算原理如图K5-1所示.设f(x)=(0x)x-(2x).则f(2)=________;f(x)在区间[-2,2]上的最小值为________.
图K5-1
13. 已知函数f(x)=(a是常数且a>0).对于下列命题:①函数f(x)的最小值是-1;②函数f(x)在R上是单调函数;③若f(x)>0在上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2,恒有f<.其中正确命题的序号是________.
14.(10分)已知函数f(x)=-(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)在上的值域是,求a的值.
15.(13分)已知定义域为[0,1]的函数f(x)同时满足:①对于任意的x∈[0,1],总有f(x)≥0;②f(1)=1;③若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2).
(1)求f(0)的值;
(2)求f(x)的最大值;
(3)若对于任意x∈[0,1],总有4f2(x)-4(2-a)f(x)+5-4a≥0成立,求实数a的取值范围.
16.(12分)已知函数f(x)自变量取值区间为A,若其值域区间也为A,则称区间A为f(x)的保值区间.
(1)求函数f(x)=x2形如[n,+∞)(n∈R)的保值区间;
(2)g(x)=x-ln(x+m)的保值区间是[2,+∞),求m的取值.
课时作业(五)
【基础热身】
1.B [解析] A选项中,函数y=x3是奇函数;B选项中,y=|x|+1是偶函数,且在(0,+∞)上是增函数;C选项中,y=-x2+1是偶函数,但在(0,+∞)上是减函数;D选项中,y
=2-|x|=|x|是偶函数,但在(0,+∞)上是减函数.故选B.
2.C [解析] 由f(x)为R上的减函数且f1,∴函数f(x)的单调递减区间为.
6.B [解析] 因为ax与loga(x+1)的单调性相同,所以不论a>1,还是00,即f(msinθ)>f(m-1),即msinθ>m-1在上恒成立.当m>0时,即sinθ>恒成立,只要0>即可,解得00在上恒成立,则2a×-1>0,a>1,③正确;
由图象可知在(-∞,0)上对任意x1<0,x2<0且x1≠x2,恒有f<成立,④正确.
14.[解答] (1)证明:方法一:设x2>x1>0,
则x2-x1>0,x1x2>0.
∵f(x2)-f(x1)=-
=-=>0,
∴f(x2)>f(x1),∴f(x)在(0,+∞)上是增函数.
方法二:∵f(x)=-,
∴f′(x)=′=>0,
∴f(x)在(0,+∞)上为增函数.
(2)∵f(x)在上的值域是,
又f(x)在上单调递增,
∴f=,f(2)=2,∴a=.
15.[解答] (1)对于③,令x1=x2=0,得f(0)≤0,
又由①知f(0)≥0,∴f(0)=0.
(2)设0≤x10,即m>-2,
令g′(x)=1->0,得x>1-m,
所以g(x)在(1-m,+∞)上为增函数,
同理可得g(x)在(-m,1-m)上为减函数.
若2≤1-m,即m≤-1,则g(1-m)=2,
得m=-1,满足题意.
若2>1-m,即m>-1,
则g(2)=2,得m=-1,矛盾.
所以满足条件的m值为-1.