2020-2021学年数学新教材人教B版必修第四册课时分层作业：11

2020-2021学年数学新教材人教B版必修第四册课时分层作业：11

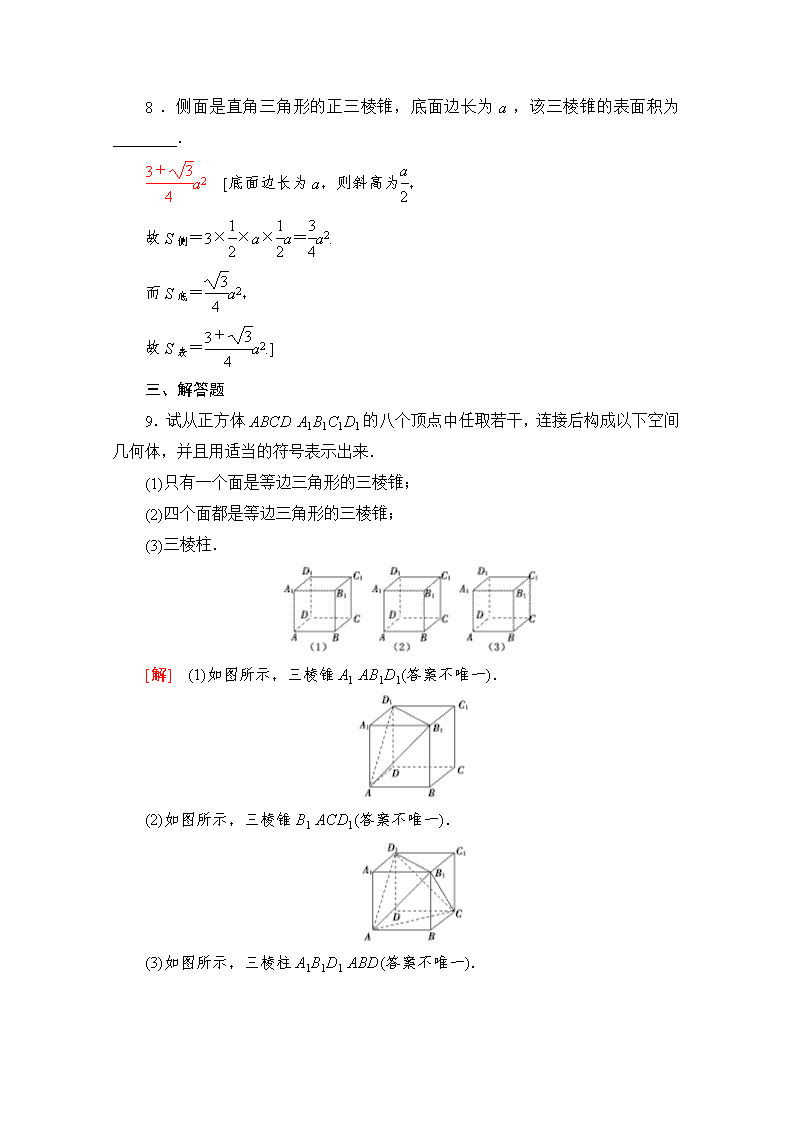
www.ks5u.com 课时分层作业(十二)　棱锥与棱台 ‎(建议用时：40分钟)‎ 一、选择题 ‎1．若一个正棱锥的各棱长和底面边长均相等，则该棱锥一定不是(　　)‎ A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥 D　[因为正六边形的边长与它的外接圆半径相等，所以满足上述条件的棱锥一定不是六棱锥．]‎ ‎2．如图所示，不是正四面体(各棱长都相等的三棱锥)的展开图的是(　　)‎ A．①③ B．②④ C．③④ D．①②‎ C　[可选择阴影三角形作为底面进行折叠，发现①②可折成正四面体，③④不论选哪一个三角形作底面折叠都不能折成正四面体．]‎ ‎3．下面说法中，正确的是(　　)‎ A．上下两个底面平行且是相似四边形的几何体是四棱台 B．棱台的所有侧面都是梯形 C．棱台的侧棱长必相等 D．棱台的上下底面可能不是相似图形 B　[由棱台的结构特点可知，A、C、D不正确．]‎ ‎4．下列三种叙述，其中正确的有(　　)‎ ‎①两个底面平行且相似，其余的面都是梯形的多面体是棱台；‎ ‎②如图所示，截正方体所得的几何体是棱台；‎ ‎③有两个面互相平行，其余四个面都是梯形的六面体是棱台．‎ A．0个 B．1个 C．2个 D．3个 A　[①不正确，因为不能保证各侧棱的延长线交于一点．②‎ 不正确，因为所得几何体两底面不相似，侧棱延长后不交于一点．③不正确，因为它们的侧棱延长后不一定交于一点，用一个平行于楔形底面的平面去截楔形，截得的几何体虽有两个面平行，其余各面是梯形，但它不是棱台．]‎ ‎5．正三棱锥的底面边长为a，高为a，则此棱锥的侧面积等于(　　)‎ A．a2 B．a‎2 C．a2 D．a2‎ A　[如图，在三棱锥SABC中，AB＝a，SO＝a，于是OD＝·AB·sin 60°＝a，从而SD＝＝，故三棱锥的侧面积为S＝3××a×＝a2.]‎ 二、填空题 ‎6．如图，已知四边形ABCD是一个正方形，E，F分别是边AB和BC的中点，沿折痕DE，EF，FD折起得到一个空间几何体，则这个空间几何体是________(只填几何体的名称)．‎ 三棱锥　[折起后是一个三棱锥(如图所示)．‎ ‎]‎ ‎7．若一个棱台共有21条棱，则这个棱台是________棱台．‎ 七　[由棱台的概念可知，棱台的上下底面为相似多边形，边数相同；侧面为梯形，侧面个数与底面多边形边数相同，可知该棱台为七棱台．]‎ ‎8．侧面是直角三角形的正三棱锥，底面边长为a，该三棱锥的表面积为________．‎ a2　[底面边长为a，则斜高为，‎ 故S侧＝3××a×a＝a2.‎ 而S底＝a2，‎ 故S表＝a2.]‎ 三、解答题 ‎9．试从正方体ABCDA1B‎1C1D1的八个顶点中任取若干，连接后构成以下空间几何体，并且用适当的符号表示出来．‎ ‎(1)只有一个面是等边三角形的三棱锥；‎ ‎(2)四个面都是等边三角形的三棱锥；‎ ‎(3)三棱柱．‎ ‎[解]　(1)如图所示，三棱锥A1AB1D1(答案不唯一)．‎ ‎(2)如图所示，三棱锥B1ACD1(答案不唯一)．‎ ‎(3)如图所示，三棱柱A1B1D1ABD(答案不唯一)．‎ ‎10．如图，正四棱台AC′的高是 ‎17 cm，两底面的边长分别是‎4 cm和‎16 cm，求这个棱台的侧棱长和斜高．‎ ‎[解]　设棱台两底面的中心分别是O′和O，B′C′，BC的中点分别是E′，E.连接O′O，E′E，O′B′，OB，O′E′，OE，则四边形OBB′O′，OEE′O′都是直角梯形．‎ 在正方形ABCD中，BC＝‎16 cm，‎ 则OB＝‎8 cm，OE＝‎8 cm；‎ 在正方形A′B′C′D′中，B′C′＝‎4 cm，‎ 则O′B′＝‎2 cm，O′E′＝‎2 cm.‎ 在直角梯形O′OBB′中，BB′＝＝＝19(cm)．‎ 在直角梯形O′OEE′中，EE′＝＝＝5(cm)．‎ 即这个棱台的侧棱长为‎19 cm，斜高为‎5 cm.‎ ‎11．(多选题)对有两个面互相平行，其余各面都是梯形的多面体，下列说法正确的是(　　)‎ A．可能是棱锥 B．可能是棱台 C．一定不是棱锥 D．一定不是棱柱 BCD　[有两个面互相平行，故此多面体一定不是棱锥，其余各面都是梯形，所以也不是棱柱，棱柱的侧面都是平行四边形，选B、C、D．]‎ ‎12．若棱长为1的正四面体ABCD中，M和N分别是边AB和CD的中点，则线段MN的长度为(　　)‎ A． B． C． D．2‎ A　[如图，连接AN，BN，‎ ‎∵正四面体ABCD的棱长为1，N是CD的中点，‎ ‎∴BN＝AN＝.‎ ‎∵M是AB的中点，∴MN⊥AB，‎ ‎∴MN＝＝＝.]‎ ‎13．已知正三棱锥的高是‎10 cm，底面积是‎12 cm2，则它的侧棱长是________cm.‎ ‎2 　[如图，已知三棱锥高SO＝‎10 cm，S正△ABC＝12，∴底面正三角形边长BC＝4.又O为△ABC中心，∴OC＝CD＝··4＝4.‎ 在Rt△SOC中，SC＝＝＝2.]‎ ‎14．在如图所示的三棱锥ABCD中，BD＝2，DC＝3，∠DAB＋∠BAC＋∠DAC＝90°，∠ADB＝∠BDC＝∠ADC＝90°.现有一只蚂蚁从点D出发经三棱锥ABCD的三个侧面绕行一周后回到点D，则蚂蚁爬行的最短距离为________．‎ ‎5　[三棱锥的侧面展开图如图(实线部分)所示．‎ 由题意知，蚂蚁爬行的最短距离即为DD′.‎ ‎∵∠DAB＋∠BAC＋∠DAC＝90°，‎ ‎∴∠DAD′＝90°.‎ ‎∵∠ADB＝∠BDC＝∠ADC＝90°且AD＝AD′，‎ ‎∴四边形ADED′为正方形．‎ 由题意，得BC＝＝，‎ 设CE＝x，则BE＝.‎ ‎∵DE＝D′E，‎ ‎∴3＋x＝2＋，解得x＝2，‎ ‎∴DE＝D′E＝5，‎ ‎∴DD′＝＝5.]‎ ‎15．设正三棱锥SABC的侧面积是底面积的2倍，正三棱锥的高SO＝3，求此正三棱锥的表面积．‎ ‎[解]　如图所示，设正三棱锥的底面边长为a，斜高为h′，过O作OE⊥AB，垂足为E，连接SE，则SE＝h′.‎ ‎∵S侧＝2S底，∴3×ah′＝a2×2，∴a＝h′.‎ ‎∵SO⊥OE，且OE＝×a＝×h′＝，‎ ‎∴由SO2＋OE2＝SE2，得32＋＝h′2，‎ ‎∴h′＝2，a＝h′＝6，‎ ‎∴S底＝a2＝×62＝9，S侧＝2S底＝18，‎ ‎∴S表＝S侧＋S底＝18＋9＝27.‎