- 2021-07-01 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修3教案:1_1_2程序框图(教、学案)
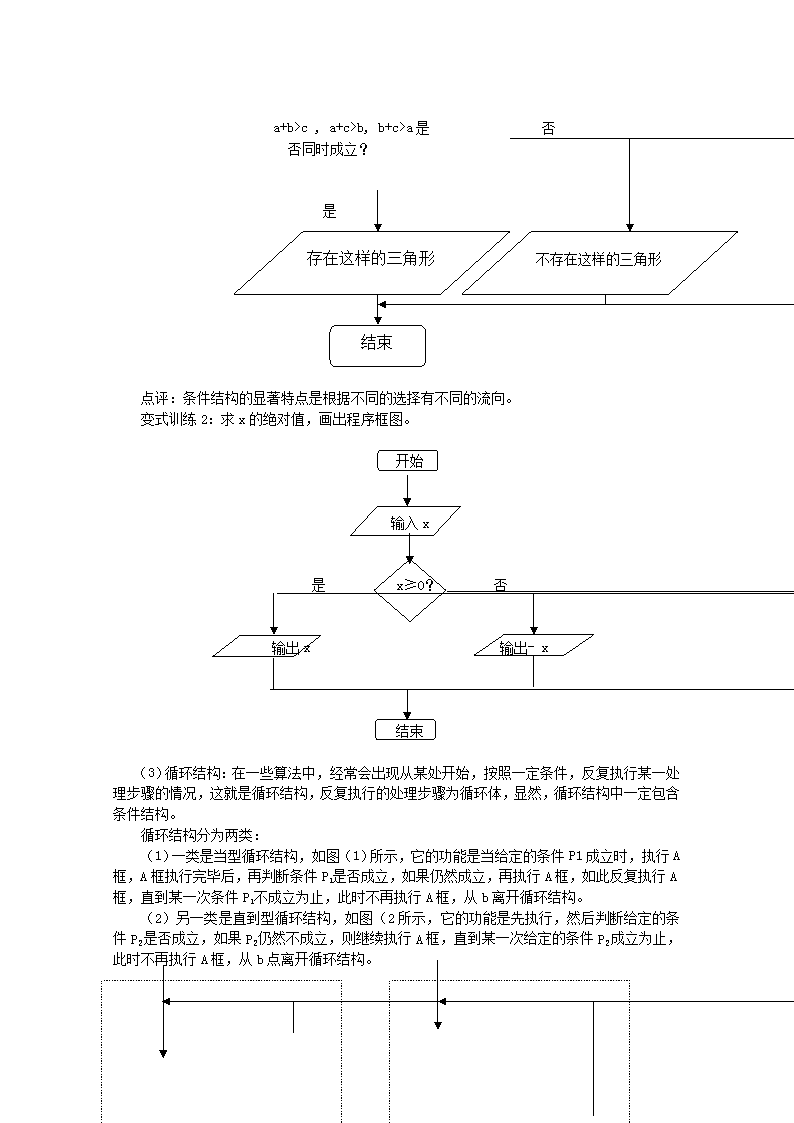
1. 1.2程序框图 [教学目标]: 1.掌握程序框图的概念;会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构;掌握画程序框图的基本规则,能正确画出程序框图。 2.通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程;学会灵活、正确地画程序框图。 3.通过本节的学习,使我们对程序框图有一个基本的了解;掌握算法语言的三种基本逻辑结构,明确程序框图的基本要求;认识到学习程序框图是我们学习计算机的一个基本步骤,也是我们学习计算机语言的必经之路。 [教学重难点]: 教学重点:程序框图的基本概念、基本图形符号和3种基本逻辑结构。 教学难点:能综合运用这些知识正确地画出程序框图。 [教学过程]: 一、.创设情境:如果你向全班同学介绍一下你心中偶像的形象,你认为用语言描述好还是拿出偶像的照片给同学们看好?说明一下你的理由算法除了用自然语言表示外,还可用程序框图表示。 二、基本概念: (1)起止框图: 起止框是任何流程图都不可缺少的,它表明程序的开始和结束,所以一个完整的流程图的首末两端必须是起止框。 (2)输入、输出框: 表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置。 (3)处理框: 它是采用来赋值、执行计算语句、传送运算结果的图形符号。 (4)判断框: 判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y”与“N”)两个分支。 三、算法的基本逻辑结构 (1)顺序结构:顺序结构描述的是是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的。 例1:已知一个三角形的三边分别为2、3、4,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图。 算法分析:这是一个简单的问题,只需先算出p的值,再将它代入公式,最后输出结果,只用顺序结构就能够表达出算法。 J 解:程序框图: 开始 p=(2+3+4)/2222 2 s=√p(p-2)(p-3)(p-4) 输出s 结束 点评:顺序结构是由若干个依次执行的步骤组成的,是任何一个算法都离不开的基本结构。 变式训练1:输入矩形的边长求它的面积,画出程序框图。 开始 输入a,b S=a*b 输出s 结束 (2)条件结构:根据条件选择执行不同指令的控制结构。 例2:任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的程序框图。 算法分析:判断分别以这3个数为三边边长的三角形是否存在,只需要验收这3个数当中任意两个数的和是否大于第3个数,这就需要用到条件结构。 程序框图: 开始 输入a,b,c a+b>c , a+c>b, b+c>a是 否 否同时成立? 是 不存在这样的三角形 存在这样的三角形 结束 点评:条件结构的显著特点是根据不同的选择有不同的流向。 变式训练2:求x的绝对值,画出程序框图。 开始 输入x 是 x≥0? 否 输出x 输出- x 结束 (3)循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。 循环结构分为两类: (1)一类是当型循环结构,如图(1)所示,它的功能是当给定的条件P1成立时,执行A框,A框执行完毕后,再判断条件P1 是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P1 不成立为止,此时不再执行A框,从b离开循环结构。 (2)另一类是直到型循环结构,如图(2所示,它的功能是先执行,然后判断给定的条件P2是否成立,如果P2 仍然不成立,则继续执行A框,直到某一次给定的条件P2成立为止,此时不再执行A框,从b点离开循环结构。 A A P1? P2? 不成立 不成立 成立 b b 当型循环结构 直到型循环结构 (1) (2) 例3:设计一个计算1+2+…+100的值的算法,并画出程序框图。 算法分析:只需要一个累加变量和一个计数变量,将累加变量的初始值为0,计数变量的值可以从1到100。 解:程序框图: 开始 i=1 Sum=0 i=i+1 Sum=sum+i i≤100? 否 是 输出sum 结束 点评:循环结构包含条件结构。 变式训练3:画出求21+22+23+…2100的值的程序框图。 解:程序框图: 开始 i=1 p=0 i=i+1 p=p+2i i≥100? 否 是 输出p 结束 四、课堂小结: 本节课主要讲述了程序框图的基本知识,包括常用的图形符号、算法的基本逻辑结构,算法的基本逻辑结有三种,即顺序结构、条件结构和循环结构。其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,它们共同构成了算法的基本结构,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达 五、布置作业: 1.输入3个实数按从大到小的次序排序。 解:程序框图: (2) 结 束 i= i +1 (1) 开 始 是 输出 s 否 i = 1 P = 1 S= 0 S= s + p (2题图) 2.给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 将上面给出的程序框图补充完整. (1)________i < = 50_________________ (2)_____p= p + i____________________ 1.1.2程序框图导学案 课前预习学案 一、预习目标: 1.了解程序框图的概念及其基本程序框图的功能; 2.知道算法的三个基本逻辑结构 二、预习内容: 1.什么是程序框图? 2.算法的基本逻辑结构有哪些? 三、提出疑惑:如何画程序框图? 课内探究学案 一、学习目标: 1.掌握程序框图的概念及其基本程序框图的功能; 2.会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构; 3.理解程序框图的顺序结构; 二、学习重点: 1. 程序框图的顺序结构的画法; 2.程序框图的概念及其基本程序框图的功能; 学习难点: 正确地画出程序框图的顺序结构。 三、学习过程: 1.情境问题: 如果你向全班同学介绍一下你心中偶像的形象,你认为用语言描述好还是拿出偶像的照片给同学们看好?说明一下你的理由。 2.新课探究: (1).右边的程序框图(如图所示),能判断任意输入的数x的 奇偶性,请大家参考书本第六页的表格,填下表: (2).你能用语言描述一下框图的基本结构特征吗? 程序框 名称 功能 m=0 m=0? (3).通过以上算法与上一节课比较,你觉得用框图来表达算法有哪些特点? (4).请大家观察、研究下面分解框图,能你总结出各有什么特点吗? 不成立 P 成立 A A B 否 P 是 A B (1)顺序结构: ; (2)条件结构: ; (3)循环结构: ; 例1:已知一个三角形的三边分别为2、3、4,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图。 变式训练1:输入矩形的边长求它的面积,画出程序框图。 例2:任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的程序框图。 变式训练2:求x的绝对值,画出程序框图。 例3:设计一个计算1+2+…+100的值的算法,并画出程序框图。 变式训练3:画出求21+22+23+…2100的值的程序框图。 3.课堂小结 (1).程序框图: (2).算法的基本逻辑结构: 4.当堂检测 (1)写出下面2个程序框图的作用: (2)写出下面2个程序框图的运行结果: 开始 开始 a=2 结束 输出S b=4 a,b S=a/b+b 输入R b= 开始 结束 输出sum a ,b abaa,b sum=a+b a=2b 输出a 结束 答案: (1)输入三个数,输出最大的一个; 输入a,b,求其和并输出。 (2)4.5; 课后练习与提高 1.流程图中的判断框,有1个入口和( )个出口. A.1 B.2 C.3 D.4 2.以下给出对程序框图的几种说法:①任何一个程序框图都必须有起止框;②输人框只能放在开始框后,输出框只能放在结束框前;③判断框是唯一具有超过一个退出点的符号;④对于一个程序来说,判断框内的条件表述方法是唯一的.其中正确说法的个数是( ). A.1 B.2 C.3 D.4 3.算法的三种基本结构是( ). A.顺序结构、流程结构、循环结构 B.顺序结构、分支结构、嵌套结构 C.顺序结构、条件结构、循环结构 D.流程结构、分支结构、循环结构 4. 若输入的a、b、c分别是21、32、75,则输出的a、b、c分别是: 5. 用代表第个学生学号,用 代表成绩,打印出每个班及格学生的学号和成绩,画出程序框图.查看更多