2019年高考数学练习题汇总10+7满分练(8)
10+7满分练(8)
1.已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B等于( )
A.(-2,0) B.(0,2) C.(-1,2) D.(-2,-1)
答案 C
解析 由x+1>0,得x>-1,
∴A=(-1,+∞),B={x||x|<2}=(-2,2),
∴A∩B=(-1,2).故选C.
2.已知a∈R,i是虚数单位.若z=a+i,z·=4,则a等于( )
A.1或-1 B.或- C.- D.
答案 A
解析 ∵z·=4,∴|z|2=4,即|z|=2.
∵z=a+i,∴|z|==2,∴a=±1.故选A.
3.在△ABC中,“sin A>sin B”是“cos A
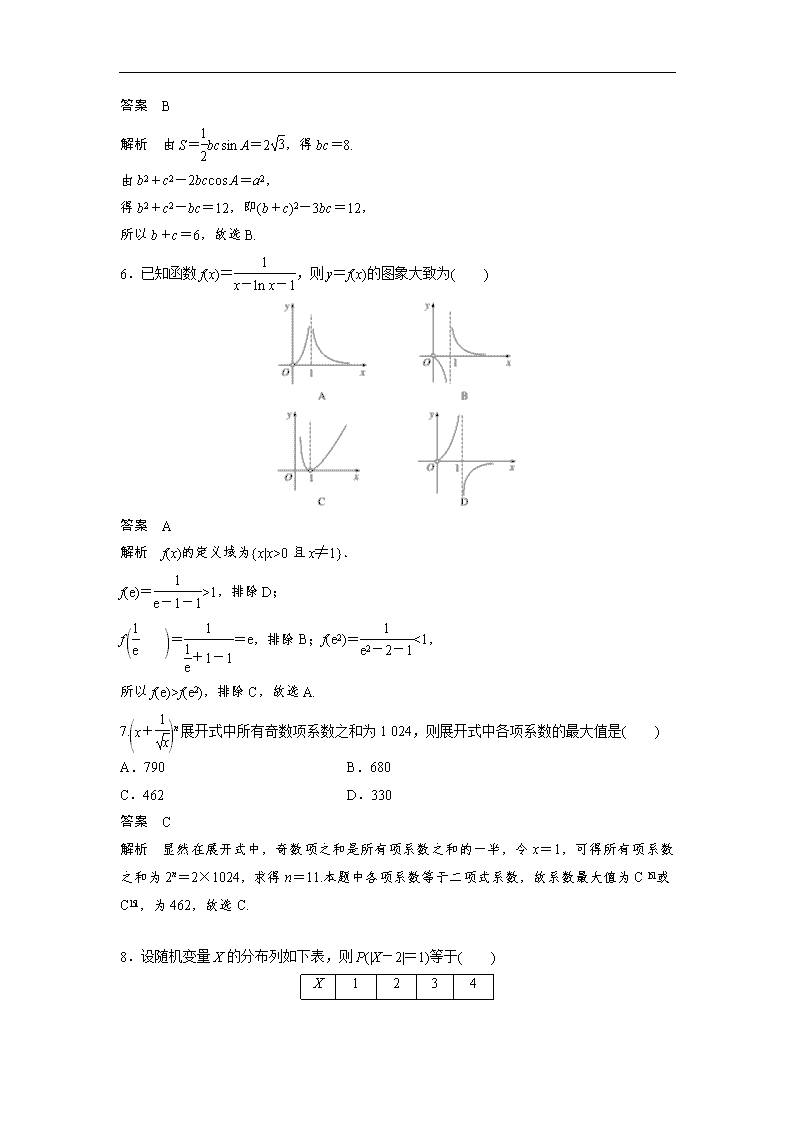
sin B⇔a>b⇔A>B,又因为在(0,π)内函数f(x)=cos x单调递减,所以A>B⇔cos Asin B⇔A>B⇔cos A0且x≠1}.
f(e)=>1,排除D;
f ==e,排除B;f(e2)=<1,
所以f(e)>f(e2),排除C,故选A.
7.n展开式中所有奇数项系数之和为1 024,则展开式中各项系数的最大值是( )
A.790 B.680
C.462 D.330
答案 C
解析 显然在展开式中,奇数项之和是所有项系数之和的一半,令x=1,可得所有项系数之和为2n=2×1024,求得n=11.本题中各项系数等于二项式系数,故系数最大值为C或C,为462,故选C.
8.设随机变量X的分布列如下表,则P(|X-2|=1)等于( )
X
1
2
3
4
P
m
A. B.
C. D.
答案 C
解析 由|X-2|=1,解得X=3或X=1,
所以P(|X-2|=1)=P(X=3)+P(X=1)=m+.
又由分布列的性质知,++m+=1,
所以m+=,
所以P(|X-2|=1)=,故选C.
9.已知实数a,b,c满足a2+2b2+3c2=1,则a+2b的最大值是( )
A. B.2 C. D.3
答案 A
解析 由a2+2b2+3c2=1,可得0≤a2+2b2≤1,
令a2+2b2=r2∈[0,1],a=rcos θ,b=rsin θ,
则a+2b=rcos θ+rsin θ=r=rsin(θ+φ)≤,
当r=1,sin(θ+φ)=1时取等号,
所以a+2b的最大值是,故选A.
10.设函数f(x)=x2+ax+b(a,b∈R)的两个零点为x1,x2,若|x1|+|x2|≤2,则( )
A.|a|≥1 B.|b|≤1
C.|a+2b|≥2 D.|a+2b|≤2
答案 B
解析 当b=0时,f(x)=x2+ax的两个零点x1=0,x2=-a,此时|x1|+|x2|=|-a|≤2,当a=时,排除A和C;当a=-,b=-时,f(x)=x2-x-=,x1=-,x2=满足|x1|+|x2|≤2,但|a+2b|==>2,排除D,故选B.
11.函数f(x)=2cos-1的对称轴为______________,最小值为________.
答案 x=kπ-(k∈Z) -3
解析 由x+=kπ(k∈Z),得x=kπ-(k∈Z),
即函数f(x)的对称轴为x=kπ-(k∈Z).
因为2cos∈[-2,2],所以2cos-1∈[-3,1],
所以函数f(x)的最小值为-3.
12.设等比数列{an}的首项a1=1,且4a1,2a2,a3成等差数列,则公比q=________;数列{an}的前n项和Sn=________.
答案 2 2n-1
解析 因为a1=1,且4a1,2a2,a3成等差数列,所以4a2=4a1+a3,即4q=4+q2,解得q=2,所以Sn==2n-1.
13.在平面直角坐标系中,A(a,0),D(0,b),a≠0,C(0,-2),∠CAB=90°,D是AB的中点,当A在x轴上移动时,a与b满足的关系式为________;点B的轨迹E的方程为________.
答案 a2=2b y=x2(x≠0)
解析 ∵∠CAB=90°,
∴·=-1,∴a2=2b.①
设B(x,y),∵D是AB的中点,
∴∴②
把②代入①,得y=x2(x≠0),∴点B的轨迹E的方程为y=x2(x≠0).
14.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积为________cm3,表面积为________cm2.
答案 24
解析 由三视图可知,该几何体为一个直三棱柱上边截去一个底面直角边分别为3,4的直角三角形、高为3的三棱锥后剩余的部分,
结合题中的数据,易得该几何体的体积为×3×4×5-××3×4×3=24(cm3),表面积为×3×4+5×5+×(2+5)×4+×(2+5)×3+×3×=(cm2).
15.函数f(x),g(x)的定义域都是D,直线x=x0(x0∈D)与y=f(x),y=g(x)的图象分别交于A,B两点,若|AB|的值是不等于0的常数,则称曲线y=f(x),y=g(x)为“平行曲线”,设f(x)=ex-aln x+c(a>0,c≠0),且y=f(x),y=g(x)为(0,+∞)上的“平行曲线”,g(1)=e,g(x)在(2,3)上的零点唯一,则a的取值范围是________.
答案
解析 因为y=f(x),y=g(x)为(0,+∞)上的“平行曲线”,所以函数g(x)是由函数f(x)的图象经过上下平移得到的,即g(x)=f(x)+m=ex-aln x+c+m,又g(1)=e-aln 1+c+m=e+c+m=e,所以c+m=0,即g(x)=ex-aln x,由g(x)=ex-aln x=0,得a=,令h(x)=,x∈(2,3),则g(x)在(2,3)上有唯一零点等价于函数y=h(x)的图象与函数y=a的图象在(2,3)上有唯一交点,h′(x)=,当x>2时,h′(x)>0,函数h(x)在(2,3)上单调递增,则h(2)
查看更多