云南省云天化中学、下关一中2021届高三复习备考联合质量检测卷（二）数学（文）试题 Word版含解析

云南省云天化中学、下关一中2021届高三复习备考联合质量检测卷（二）数学（文）试题 Word版含解析

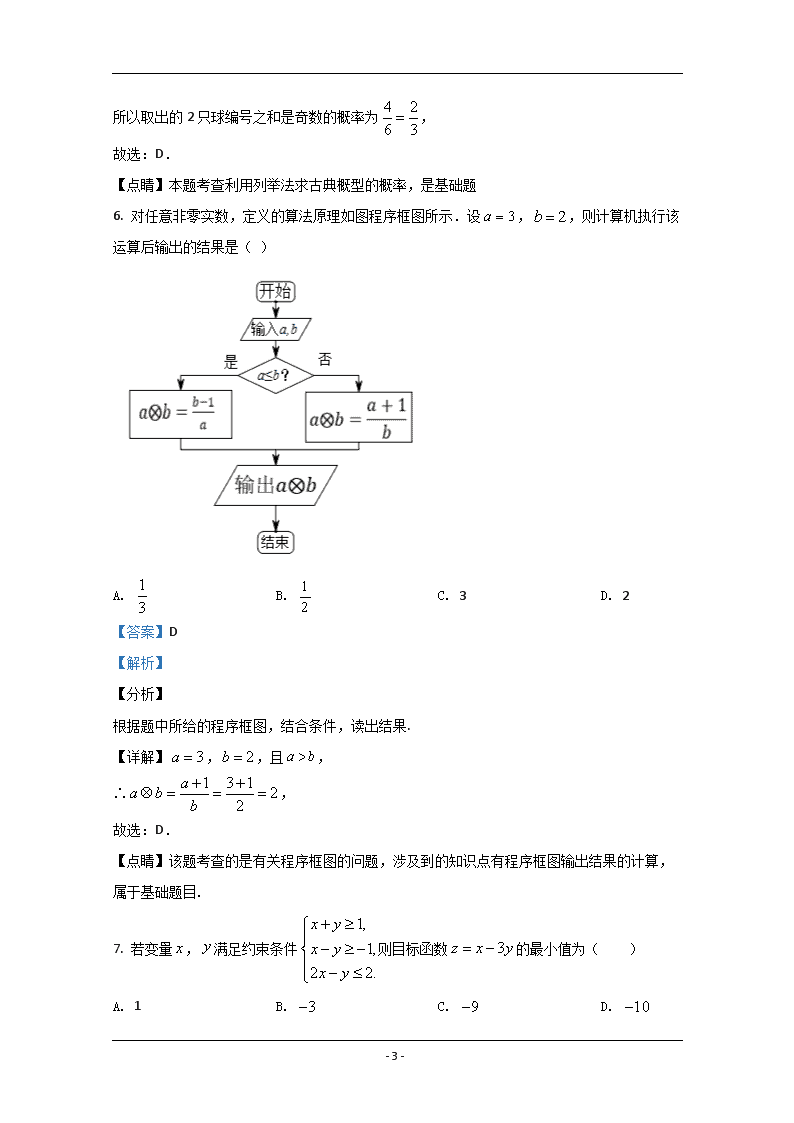
- 1 - 文科数学 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题所给的四个选项 中，只有一项是符合题目要求的） 1. 设集合 ， ，则 （ ） A. B. C. D. 【答案】A 【解析】 【分析】 根据集合交集的定义，结合题中所给的集合中的元素，求得结果. 【详解】 ， ，则 ， 故选：A． 【点睛】该题考查的是有关集合的问题，涉及到的知识点有集合的运算，属于基础题目. 2. 设复数 ， 在复平面内的对应点关于实轴对称， ．则 （ ） A. B. 5 C. D. 13 【答案】D 【解析】 【分析】 由题意求出 ，结合复数的乘法运算即可求出 . 【详解】由题意，得 ，则 ， 故选:D． 【点睛】本题考查了复数的计算，属于基础题.本题的关键是求出 . 3. 设向量 ， 满足 ， ，则 （ ） A. 14 B. C. 12 D. 【答案】B 【解析】 【分析】 { }1,0,1A = − { }1,2,3,4B = − A B = { }1− { }0 { }1 ∅ { }1,0,1A = − { }1,2,3,4B = − { }1A B∩ = − 1z 2z 1 2 3iz = + 1 2z z = 5− 13− 2z 1 2z z 2 2 3iz = − ( )( )1 2 2 3i 2 3i 13z z = + − = 2z a b 6a b− =r r 2a b⋅ =  a b+ =  14 2 3 - 2 - 利用配方法转化为 ，代入已知可解得结 果. 【详解】因为 ， 所以 ， 故选：B． 【点睛】本题平面向量数量积的运算律，考查了求向量的模长，属于基础题. 4. 化简 的值为（ ） A. B. C. D. 【答案】C 【解析】 【分析】 根据两角和余弦公式化简求值即可. 【详解】 ， 故选 C． 【点睛】本题考查了三角恒等变换，逆用两角和余弦公式化简求值，属于简单题. 5. 袋中共有完全相同 4 只小球、编号为 1，2，3，4，现从中任取 2 只小球，则取出的 2 只 球编号之和是奇数的概率为（ ） A. B. C. D. 【答案】D 【解析】 【分析】 先列举出任取 2 只小球的事件，共 6 种取法，再列举出 2 只球编号之和是奇数的事件，共 4 种取法，最后求取出的 2 只球编号之和是奇数的概率即可. 【详解】解：在编号为 1，2，3，4 的小球中任取 2 只小球，则有 ， ， ， ， ， ，共 6 种取法， 则取出的 2 只球编号之和是奇数的有 ， ， ， ，共 4 种取法， 的 ( ) ( )2 22 2 2 2 4a b a b a b a b a b a b+ = + = + + ⋅ = − + ⋅            ( ) ( )2 22 2 2 2 4a b a b a b a b a b a b+ = + = + + ⋅ = − + ⋅            6 4 2 14= + × = 2 14a b+ =  cos16 cos44 sin16 sin 44−° ° ° ° 3 2 3 2 − 1 2 1 2 − ( ) 1cos16 cos44 sin16 sin 44 cos 16 44 cos60 2 ° °− ° ° = °+ ° = ° = 2 5 3 5 1 3 2 3 { }1,2 { }1,3 { }1,4 { }2,3 { }2,4 { }3,4 { }1,2 { }1,4 { }2,3 { }3,4 - 3 - 所以取出的 2 只球编号之和是奇数的概率为 ， 故选：D． 【点睛】本题考查利用列举法求古典概型的概率，是基础题 6. 对任意非零实数，定义的算法原理如图程序框图所示．设 ， ，则计算机执行该 运算后输出的结果是（ ） A. B. C. 3 D. 2 【答案】D 【解析】 【分析】 根据题中所给的程序框图，结合条件，读出结果. 【详解】 ， ，且 ， ∴ ， 故选：D． 【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有程序框图输出结果的计算， 属于基础题目. 7. 若变量 ， 满足约束条件 则目标函数 的最小值为（ ） A. 1 B. C. D. 4 2 6 3 = 3a = 2b = 1 3 1 2 3a = 2b = a b> 1 3 1 22 aa b b + +⊗ = = = x y 1, 1, 2 2. x y x y x y + ≥  − ≥ −  − ≤ 3z x y= − 3− 9− 10− - 4 - 【答案】C 【解析】 【分析】 画出可行域，结合图形分析最优解，从而求出最小值. 【详解】画出可行域，向上平移基准直线 ,可得最优解为 ， 由此求得目标函数的最小值为 ， 故选:C． 【点睛】本题考查了线性规划求最值，属于基础题. 8. 已知函数 ，则函数 的图象在点 处的切线斜率为（ ） A. B. C. D. 【答案】C 【解析】 【分析】 根据 得到它的导函数 ，求 即可. 【详解】依据 ，有 ， 因此，函数 的图象在点 处的切线斜率为 ， 故选 C． 【点睛】本题考查了根据导数的几何意义求函数在某点处的切线斜率，属于简单题. 9. 某几何体的三视图如图所示，则该几何体的体积为（ ） 3 0x y− = ( )3,4A 3 3 4 9z = − × = − ( ) 2 1ln 1 2f x x x x= + − ( )f x ( )( ),e f e 1 2 1 2 − 13 2e − 1 32 e− ( )f x ( )f x¢ ( )f e′ ( ) 2 1ln 1 2f x x x x= + − ( ) 12 ln 2f x x x x′ = + − ( )y f x= ( )( ),e f e ( ) 13 2k f e e′= = − - 5 - A. B. C. D. 【答案】A 【解析】 【分析】 由三视图可知几何体：圆台，进而依据圆台的体积公式求体积即可. 【详解】该几何体为上、下底面直径分别为 2、4，高为 4 的圆台， ∴体积为 ， 故选 A． 【点睛】本题考查了根据三视图求几何体的体积，圆台的体积公式应用，属于简单题. 10. 已知 是双曲线 ： 的一个焦点，则点 到 的一条渐近线的距 离为（ ） A. B. 3 C. D. 【答案】A 【解析】 【分析】 根据题意，由双曲线的几何性质可得焦点坐标以及渐近线的方程，进而由点到直线的距离公 式计算可得答案． 【详解】双曲线 ： 的方程化为： . 所以双曲线 的焦点在 轴上，且 . 渐近线方程为： ， 28 3 π 25 3 π 28π 25π ( )2 21 284 2 1 2 13 3V ππ= × × + + × = F C 2 2 5 ( 0)x my m m− = > F C 5 5m 5m C 2 2 5 ( 0)x my m m− = > 2 2 15 5 x y m − = ( 0)m > C x 5 5c m= + x my= ± - 6 - 取 的坐标为 ，取一条渐近线 . 则点 到 的一条渐近线的距离 ， 故选：A 【点睛】本题考查双曲线的几何性质，关键是利用双曲线的标准方程，计算出焦点坐标以及 渐近线的方程．属于基础题. 11. 在正方体 中，点 为线段 的中点，则异面直线 与 所成角 的余弦值为（ ） A. 0 B. C. D. 【答案】C 【解析】 【分析】 连接 ，找出异面直线所成的角，结合余弦定理即可求出所成角的余弦值. 【详解】连接 ，则 ，则 为所求，设正方体棱长为 2， 在 中， ， ， ， 所以 ， 故选:C． 【点睛】本题考查了异面直线所成角的求解，考查了余弦定理，属于基础题.本题的关键是找 出异面直线所成的角. F ( 5 5,0)m + + =0x my F C 5 5 5 1 md m += = + 1 1 1 1ABCD A B C D− E AB 1A D EC 1 2 10 5 11 16 1 1, ,B C B E CE 1 1, ,B C B E CE 1 1//B C A D 1B CE θ∠ = 1B CE△ 5EC = 1 5B E = 1 2 2=B C 5 8 5 2 10cos 52 5 2 2 10 θ + −= = = × × - 7 - 12. 设函数 ，函数 ，若对于 ， ，使 成立，则实数 的取值范围是（ ） A. B. C. D. 【答案】A 【解析】 【分析】 由题意只需 ，对函数 求导，判断单调性求出最小值，对函数 讨 论对称轴和区间 的关系，得到函数最小值，利用 即可得到实数 的取 值范围. 【详解】若对于 ， ，使 成立，只需 ， 因为 ，所以 ，当 时， ，所以 在 上是减函数，所以函数 取得最小值 ． 因为 ， 当 时， 在 上单调递增，函数取得最小值 ，需 ，不成立； 当 时， 在 上单调递减，函数取得最小值 ，需 ，解得 ，此时 ； 当 时， 在 上单调递减，在 上单调递增，函数取得最小值 ，需 ，解得 或 ，此时无解； 综上，实数 的取值范围是 ， 故选:A． 【点睛】本题考查利用导数研究函数的最值，考查二次函数在区间的最值的求法，考查分类 讨论思想和转化思想，属于中档题. 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分） ( ) 31 143 3f x x x= − + ( ) 2 2 1g x x bx= − + [ ]1 1,2x∀ ∈ [ ]2 0,1x∃ ∈ ( ) ( )1 2f x g x≥ b 7 ,2  +∞  5 ,8  +∞  7, 2  −∞   5, 8  −∞   ( ) ( )min minf x g x≥ ( )f x ( )g x [ ]0,1 ( ) ( )min minf x g x≥ b [ ]1 1,2x∀ ∈ [ ]2 0,1x∃ ∈ ( ) ( )1 2f x g x≥ ( ) ( )min minf x g x≥ ( ) 31 143 3f x x x= − + ( ) 2 4f x x′ = − [ ]1,2x∈ ( ) 0f x′ ≤ ( )f x [ ]1,2 ( )f x ( )2 5f = − ( ) ( )22 22 1 1g x x bx x b b= − + = − + − 0b ≤ ( )g x [ ]0,1 ( )0 1g = 5 1− ≥ 1b ≥ ( )g x [ ]0,1 ( )1 2 2g b= − 5 2 2b− ≥ − 7 2b ≥ 7 2b ≥ 0 1b< < ( )g x [ ]0,b ( ],1b ( ) 21g b b= − 25 1 b− ≥ − 6b ≤ − 6b ≥ b 7 ,2  +∞  - 8 - 13. 已知函数 ．则 的值为______． 【答案】 【解析】 【分析】 根据题中所给的函数解析式，将自变量代入求得结果. 【详解】因为 ，所以 ． 故答案为： . 【点睛】该题考查的是有关函数的问题，涉及到的知识点有已知自变量求函数值，属于基础 题目. 14. 函数 的最大值为______. 【答案】7 【解析】 【分析】 由题得 ，再利用二次函数的图象和性质求最值. 【详解】由题得 ∴当 时， 取得最大值 7. 故答案为：7 【点睛】本题主要考查二倍角的余弦公式的应用，考查二次型复合函数的最值的求法，意在 考查学生对这些知识的理解掌握水平. 15. 已知偶函数 在 上单调递减． ．若 ．则 的取值范围 是______． 【答案】 【解析】 【分析】 根据奇偶性和单调性可得 ，从而得 ，即可得解. ( ) lnf x x x= ( )f e e ( ) lnf x x x= ( )f e e= e ( ) cos2 6cosf x x x= − ( ) 23 112 cos 2 2xf x  = − −   ( ) 2 2 3 112cos 6cos 1 2 cos 2 2f x xx x  = − − = − −   cos 1x = − ( )f x ( )f x [ )0,+∞ ( )1 0f = ( )2 0f x − > x ( )1,3 ( ) ( )2 1f x f− > 2 1x − < - 9 - 【详解】因为 是偶函数，所以不等式 ， 又因为 在 上单调递减，所以 ，解得 ． 故答案为： . 【点睛】本题主要考查了奇偶性和单调性的应用，属于基础题. 16. 在 中， ， ，则中线 的取值范围是______． 【答案】 【解析】 【分析】 由正弦定理可得 ，从而可求出 的轨迹方程，结合椭圆的性质即可求出中线的取值 范围. 【详解】由正弦定理得 ，则点 是以 ， 为焦点的椭圆上的一点， 不妨以 ， 所在直线为 轴，点 为原点建立平面直角坐标系，则椭圆方程为 ， 由椭圆的性质可知，椭圆上点到原点距离最大为长轴的一半，最小为短轴的一半， 则可知中线 长的取值范围为 ． 故答案为: . 【点睛】本题考查了正弦定理，考查了椭圆 性质，属于中档题.本题的难点是将中线转化为 椭圆问题. 三、解答题（共 70 分.解答应写出文字说明，证明过程或演算步骤） 17. 已知数列 为等差数列， ， ． 的 ( )f x ( ) ( ) ( )2 0 2 1f x f x f− > ⇔ − > ( )f x [ )0,+∞ 2 1x − < 1 3x< < ( )1,3 ABC 2BC = sin sin 3sinB C A+ = AD )2 2,3 6b c+ = A 3 6b c a+ = = A B C B C x D 2 2 19 8 x y+ = AD )2 2,3 )2 2,3 { }na 1 2a = 3 5 16a a+ = - 10 - （1）求数列 的通项公式； （2）设 ，求数列 的前 项和 ． 【答案】（1） ；（2） . 【解析】 分析】 （1）先建立方程组 求得 ，再求数列 的通项公式； （2）先化简 为 ，再利用“裂项相消法”求数列 的前 项和 即可 【详解】解：（1）因为 ， ，所以 ， 因为数列 为等差数列，所以 ，解得 ， 所以 ． （2）因为 ， ，所以 ， 所以 ． 【点睛】本题考查等差数列的基本量法、求等差数列的通项公式、“裂项相消法”求数列的 前 项和，是基础题. 18. 已知四边形 是梯形（如图甲）， ， ， ， ， 为 的中点，以 为折痕把 折起，使点 到达点 的位置（如图乙），且 ． 【 { }na 1 4 n n n b a a + = { }nb n nT 2na n= 1n nT n = + 1 3 5 1 2 2 6 16 a a a a d =  + = + = 2d = { }na nb 1 1 1n n − + { }nb n nT 1 2a = 3 5 16a a+ = 1 3 5 2 16 a a a =  + = { }na 1 3 5 1 2 2 6 16 a a a a d =  + = + = 2d = 2na n= 1 4 n n n b a a + = 2na n= ( ) 1 1 1 1 1nb n n n n = = −+ + 1 1 1 1 1 11 12 2 3 1 1 1n nT n n n n = − + − + + − = − =+ + + n ABCD //AB CD AD DC⊥ 4CD = 2AB AD= = E CD AE ADE D P 2PB = - 11 - 甲 乙 （1）求证：平面 平面 ； （2）求点 到平面 的距离． 【答案】（1）证明见解析；（2） . 【解析】 【分析】 （1）连接 ，取 的中点 ，连接 ， ， 可得 ， ，进而 可得 平面 ，又 平面 ，可得平面 平面 ； （2）设点 到平面 的距离为 ，利用等体积法 进行转化计算即可得解. 【详解】（1）连接 ，因为 ， ， ， 为 的中点， ，所以四边形 是边长为 2 的正方形，且 ， 取 的中点 ，分别连接 ， ， 因为 ，所以 ， ，且 ， ， 又 ，所以 ，所以 ， 又 ，所以 平面 ， 又 平面 ，所以平面 平面 ； （2）由（1）知， 平面 ， 为正三角形且边长为 2， 设点 到平面 的距离为 ， ， 则 ， PAE ⊥ ABCE A PBE 2 6 3 BE AE M PM BM PM AE⊥ PM MB⊥ PM ⊥ ABCE PM ⊂ PAE PAE ⊥ ABCE A PBE d P ABE A PBEV V− −= BE //AB CD AD DC⊥ 4CD = E CD 2AB AD= = ABED BE EC= AE M PM BM 2AP PE= = PM AE⊥ BM AE⊥ 2 2AE = 2PM AM BM= = = 2PB = 2 2 2PM MB PB+ = PM MB⊥ AE MB M∩ = PM ⊥ ABCE PM ⊂ PAE PAE ⊥ ABCE PM ⊥ ABCE PBE△ A PBE d P ABE A PBEV V− −= 1 1 3 3ABE PBES PM S d× × = × ×△ △ - 12 - 所以 ， 即 ，解得 ， 故点 到平面 的距离为 ． 【点睛】本题考查面面垂直的证明，考查点面间的距离求法，考查逻辑思维能力和计算能力， 考查空间想象能力，属于常考题. 19. 某校从参加市联考的甲、乙两班数学成绩 110 分以上的同学中各随机抽取 8 人，将这 16 人的数学成绩编成如下茎叶图. （Ⅰ）茎叶图中有一个数据污损不清（用△表示），若甲班抽出来的同学平均成绩为 122 分， 试推算这个污损的数据是多少？ （Ⅱ）现要从成绩在 130 分以上的 5 位同学中选 2 位作数学学习方法介绍，请将所有可能的 结果列举出来，并求选出的两位同学不在同一个班的概率. 【答案】（1）这个污损的数据是 ；（2）所求概率为 . 【解析】 试题分析：（1）根据平均数概念，求出污损不清的数字；（2）先选出甲乙两班分数在 130 分以上的学生共有 5 人，甲班 2 人，乙班 3 人，从 5 人中抽取 2 人共有 10 种取法，不在同一 21 1 1 3 3 2 3 4BE AB PM BE d× × × × = × × × 21 1 1 32 2 2 23 2 3 4 d× × × × = × × × 2 6 3d = A PBE 2 6 3 3 3 5 - 13 - 个班的学生的取法有 6 种，则最后的概率为 . 试题解析：（1）设污损不清的数字为 ，由平均数的概念得 ，解得 . （2）依据题意，甲班 分以上的有 人，编号为 ， ，乙班 分以上的有 人，编号 为 、 、 ，从 位同学中任选 人，所有的情况列举如下： , , , , , , , , , 共 10 种结果 其中两位同学不在同一班的有 , , , , , 共 6 种 所以所求概率为 . 考点：对茎叶图的理解，平均数，古典概型的求解. 20. 已知抛物线 ： 的焦点为 ， 为坐标原点．过点 的直线 与抛物线 交于 ， 两点． （1）若直线 与圆 ： 相切，求直线 的方程； （2）若直线 与 轴的交点为 ．且 ， ，试探究： 是否为定 值？若为定值，求出该定值；若不为定值，试说明理由． 【答案】（1） ；（2） ，理由见解析； 【解析】 【分析】 （1）由直线 过焦点 ，且与半径为 ，圆心 的圆相切知圆心 到直线 的距离 即可求直线斜率 ，进而得到直线方程；（2）由直线 与抛物线 、 轴的交点情况 知 斜 率 存 在 且 ， 令 ， 联 立 方 程 得 ， 又 ， ，应用向量共线的坐标表示有 即可确定 是否为定值. 【详解】（1）由题意知： 且圆 的半径为 ，圆心 ，即有 在圆 外， ∴设直线 为 ，则圆心 到直线 的距离 ， 6 10 x [110 3 120 3 130 2] 2 2 8 0 7 1 3 1228 xx × + × + × + + + + + + + += = 3x = 130 2 A B 130 3 c d e 5 2 AB Ac Ad Ae Bc Bd Be cd ce de Ac Ad Ae Bc Bd Be 6 3 10 5 = C 2 4y x= F O F l C A B l O 2 2 1 9x y+ = l l y D DA AFλ=  DB BFµ=  λ µ+ 2 ( 1)4y x= ± − 1λ µ+ = − l F 1 3r = (0,0)O O l 1 3d = k l C y 0k ≠ 1 1( , )A x y 2 2( , )B x y 1 2 1=x x DA AFλ=  DB BFµ=  1 2 ( 1)( 1)x x λµ λ µ= + + λ µ+ (1,0)F O 1 3r = (0,0)O F O l ( 1)y k x= − O l 2 | | 1 31 kd k −= = + - 14 - 解之得： ，即直线 的方程为 . （2）由过 的直线 与抛物线 交于 ， 两点，与 轴的交点为 ，即斜率存在且 ，设直线 为 ，有 ， 联立直线方程与椭圆方程，有 ，可得 ， 设 ， ，即有 ， ， ， ， ， 由 ， ，可得 ， ， ∴ ，即可得 为定值 【点睛】本题考查了抛物线，由直线与抛物线的交点情况，结合它与圆的位置关系求直线方 程，根据直线与 y 轴、抛物线的交点，结合向量共线情况说明参数之和是否为定值. 21. 已知函数 f（x）=ex﹣ax﹣1． （1）求 f（x）的单调增区间； （2）是否存在 a，使 f（x）在（﹣2，3）上为减函数，若存在，求出 a 的取值范围，若不存 在，说明理由． 【答案】（1）f（x）的递增区间是[lna，+∞）．（2）存在实数 a≥e3，使 f（x）在（﹣2，3）上 单调递减． 【解析】 试题分析：（1）先求出函数的导数，再讨论①若 a≤0，②若 a＞0 的情况，从而求出单调区 间； （2）由 f′（x）=ex﹣a≤0 在（﹣2，3）上恒成立．从而 a≥ex 在 x∈（﹣2，3）上恒成立，从而 f （x）在（﹣2，3）上为减函数，得 a≥e3．故存在实数 a≥e3，使 f（x）在（﹣2，3）上单调递 减． 解 f′（x）=ex﹣a， （1）若 a≤0，则 f′（x）=ex﹣a≥0， 2 4k = ± l 2 ( 1)4y x= ± − (1,0)F l C A B y D 0k ≠ l ( 1)y k x= − (0, )D k− 2 4 ( 1) y x y k x  =  = − 2 2 2 22( 2) 0k x k x k− + + = 1 1( , )A x y 2 2( , )B x y 1 2 1=x x 1 1( , )DA x y k= + 1 1( , )AF x yλ λ λ λ= − − 2 2( , )DB x y k= + 2 2( , )BF x yµ µ µ µ= − − DA AFλ=  DB BFµ=  1 1x λ λ= + 2 1x µ µ= + 1 2 1( 1)( 1)x x λµ λ µ= =+ + 1λ µ+ = − - 15 - 即 f（x）在 R 上递增， 若 a＞0，ex﹣a≥0，∴ex≥a，x≥ln a． 因此 f（x）的递增区间是[lna，+∞）． （2）由 f′（x）=ex﹣a≤0 在（﹣2，3）上恒成立． ∴a≥ex 在 x∈（﹣2，3）上恒成立． 又∵﹣2＜x＜3，∴e﹣2＜ex＜e3，只需 a≥e3． 当 a=e3 时 f′（x）=ex﹣e3 在 x∈（﹣2，3）上，f′（x）＜0， 即 f（x）在（﹣2，3）上为减函数， ∴a≥e3． 故存在实数 a≥e3，使 f（x）在（﹣2，3）上单调递减． 考点：利用导数研究函数的单调性． 22. 在平面直角坐标系 中，已知曲线 ： （ 为参数）．曲线 ： （ 为参数），且 ．点 为曲线 与 的公共点． （1）求动点 的轨迹方程； （2）在以原点 为极点， 轴的非负半轴为极轴的极坐标系中，直线 的极坐标方程为 ，求动点 到直线 距离的最大值． 【答案】（1） ；（2） ． 【解析】 【分析】 （ 1 ） 设 点 ， 点 P 同 时 满 足 曲 线 与 的 方 程 ， 消 参 得 ， ， ，由 ，即可求得点 的轨迹方程； （2）由 ， ，将极坐标方程转化为直角坐标方程，动点 为圆心在原 点，半径为 3 圆，先求出圆心到直线 的距离，即可求出动点 到直线 距离的最大值. 【详解】（1）设点 P 的坐标为 . 因为点 P 为曲线 与 的公共点，所以点 P 同时满足曲线 与 的方程. 的 xOy 1C 1 1 3 cos , sin . x t y t α α = − +  = 1t 2C 2 2 3 cos , sin . x t y t β β = +  = 2t tan tan 1α β = − P 1C 2C P O x l cos 2 sin 5 0ρ θ ρ θ− + = P l ( )2 2 9 3x y x+ = ≠ ± 5 3+ P ( ),x y 1C 2C 1tan 3 y x θ = + 2tan 3 y x θ = − 1 2tan tan 1θ θ = − P cosx ρ θ= siny ρ θ= P l P l ( ),x y 1C 2C 1C 2C - 16 - 曲线 消去参数可得 ，曲线 消去参数可得 . 由 ，所以 ， 所以点 的轨迹方程为 ． （2）因为直线 的极坐标方程为 ， 根据 ， 可化直线 的直角坐标方程为 ， 因为动点 的轨迹为圆 （去掉两点 ）， 圆心 到直线 的距离为 ， 所以动点 到直线 的距离的最大值为 ． 【点睛】本题主要考查动点的轨迹方程的求法、极坐标方程与直角坐标方程的互化、直线与 圆的位置关系，考查学生转化和计算能力，属于基础题. 23. 已知函数 （1）当 时，求不等式 的解集； （2）若 ，求 的取值范围． 【答案】（1） ；（2） 或 ． 【解析】 【分析】 （1）由题意 ，令 即有 求解集即可；（2）由绝对值的几何 含义知 ，则 等价于 ，即可求 的取值范围. 【详解】（1）当 时， ， 令 ，即求 解集， ∴解之得： ． 的 1C 1tan 3 y x θ = + 2C 2tan 3 y x θ = − tan tan 1α β = − 13 3 y y x x ⋅ = −+ − P ( )2 2 9 3x y x+ = ≠ ± l cos 2 sin 5 0ρ θ ρ θ− + = cosx ρ θ= siny ρ θ= l 2 5 0x y− + = P ( )2 2 9 3x y x+ = ≠ ± ( )3,0± O l 5 5 5 d = = P l 5 3+ ( ) 2 3f x x a x a= − + − + 2a = ( ) 3f x ≥ ( ) 1f x ≥ a ( ] [ ), 0 3,−∞ +∞ 2a ≤ 4a ≥ ( ) 3f x ≥ ( ) ( ) 3h x f x= − ( ) 0h x ≥ ( ) 3f x a≥ − ( ) 1f x ≥ 3 1a − ≥ a 2a = ( ) 3 2 , 1 2 1 1,1 2 2 3, 2 x x f x x x x x x − ≤ = − + − = < <  − ≥ 2 , 1 ( ) ( ) 3 2,1 2 2 6, 2 x x h x f x x x x − ≤ = − = − < <  − ≥ ( ) 0h x ≥ ( ] [ ), 0 3,−∞ +∞ - 17 - （2）因为 ， 由 ，即等价于 ， 解得 或 ． 【点睛】本题考查了解绝对值不等式，应用等价转化、绝对值的几何含义求解集、参数范围. ( ) 2 3 3f x x a x a a= − + − + ≥ − ( ) 1f x ≥ 3 1a − ≥ 2a ≤ 4a ≥