数学文科仿真模拟卷三
数学文科仿真模拟卷三
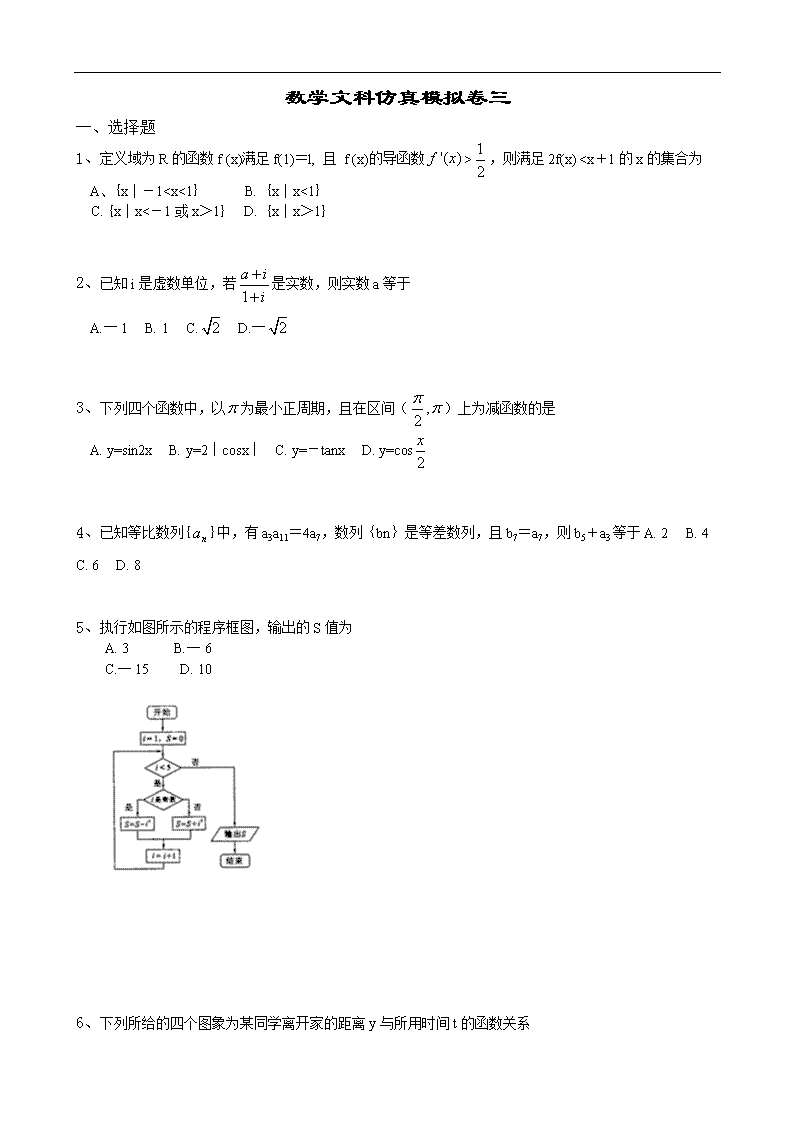
一、选择题
1、定义域为R的函数f (x)满足f(1)=l, 且 f (x)的导函数>,则满足2f(x)
0且a≠1,b>0,则“logab >0”是“(a一1)(b一1)>0”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9、一个棱锥的三视图如图(尺寸的长度单位为m),则该棱锥的体积是(单位:m3).
A. 4+2 B. 4+ C、 D、
10、已知向量=(cosθ, sinθ)与=(cosθ, -sinθ)互相垂直,且θ为锐角,则函数
f(x)=sin(2x-θ)的图象的一条对称轴是直线
A. x= B. x= C. x= D. x=
11、已知集合A={ x|lgx≤0},B= {x||x+1|>1},则A∩B=
A.(-2,1) B.(一co,一2〕U[1,+co)
C. (0,] D.(一co,-2) U (0,1]
12、在平面直角坐标系内,若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第二象限内,则实数a的取值范围为
A.(2,+∞) B.(1,十∞)
C.(一∞,一1) D.(-∞,2)
二、填空题
13、设互不相同的直线l,m,n和平面α、、,给出下列三个命题:
①若l与m为异面直线,,则α∥
②若α∥,,,则l∥m;
③若,l∥,则m∥n.
其中真命题的个数为______
14、已知实数m是2,8的等比中项,则圆锥曲线=1的离心率为___
15、在区间[-1,1]上随机取一个数k,使直线y=k(x+2)与圆x2+y2=1有公共点的概率为_____
16、设α为△ABC的内角,且tanα=-,则sin2α的值为____
三、解答题
17、
设f(x)=1n(|x-1|+m|x-2|一3) (m∈R).
(1)当m=0时,求函数f(x)的定义域;
(2)当时,是否存在m使得f (x) ≤0恒成立,若存在求出实数m的取值范
围,若不存在,说明理由.
18、已知等比数列{}的前n项和为Sn,S3=14,S6 =126.
(1)求数列{}的通项公式;
(2)设…+,试求的表达式.
19、为了搞好对水电价格的调研工作,管理部门采用了分层抽样的方法,分别从春之曲、
凤凰城、山水人家三个居民区的相关家庭中,抽取若干户家庭进行调研,有关数据见下表(单位:户)
(1)求x,y ;
(2)若从春之曲、山水人家两个片区抽取的家庭中随机选2户家庭参加实施办法的听证会,求这2户家庭分别来自春之曲、山水人家两个居民区的概率.
20、如图,四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,直线PD与底面ABCD所成的角等于300,PF=FB, E∈BC,EF∥平面PAC.
(1)试求若的值;
(2)求三棱锥P一ADC的表面积和体积
21、已知函数f (x) =x2- 2.x, g (x) 是R上的奇函数,且当x∈(-∞,0],
g(x) +fj(x)=x2.
(1)求函数g(x)在R上的解析式;
(2)若函数h(x)=x[g(x)-+]在〔0,十∞)上是增函数,且0,求的取值范围.
22、已知椭圆C:的离心率为,且过点Q(1,).
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于A,B两点,设P点在直线x+y-1=0
上,且满足 (O为坐标原点),求实数t的最小值.
23、
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE
求证:(1)BE-=DE;
(2)∠D=∠ACE.
24、
已知直线Cl: (t为参数),圆C2 : =1.(极坐标轴与x轴非负半轴重合)
(1)当时,求直线C1被圆C2所截得的弦长;
(2)过坐标原点O作C1的垂线,垂足为A.当a变化时,求A点的轨迹的普通方程.
以下是答案
一、选择题
1、 B
2、 B
3、 C
4、 D
5、 D
6、 A
7、 C
8、 C
9、 D
10、 B
11、 C
12、 A
二、填空题
13、 1
14、
15、
16、
三、解答题
17、
18、
19、
20、
21、
22、
23、
24、