- 2021-07-01 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】山东省临沂市2019-2020学年高一下学期期末考试试题
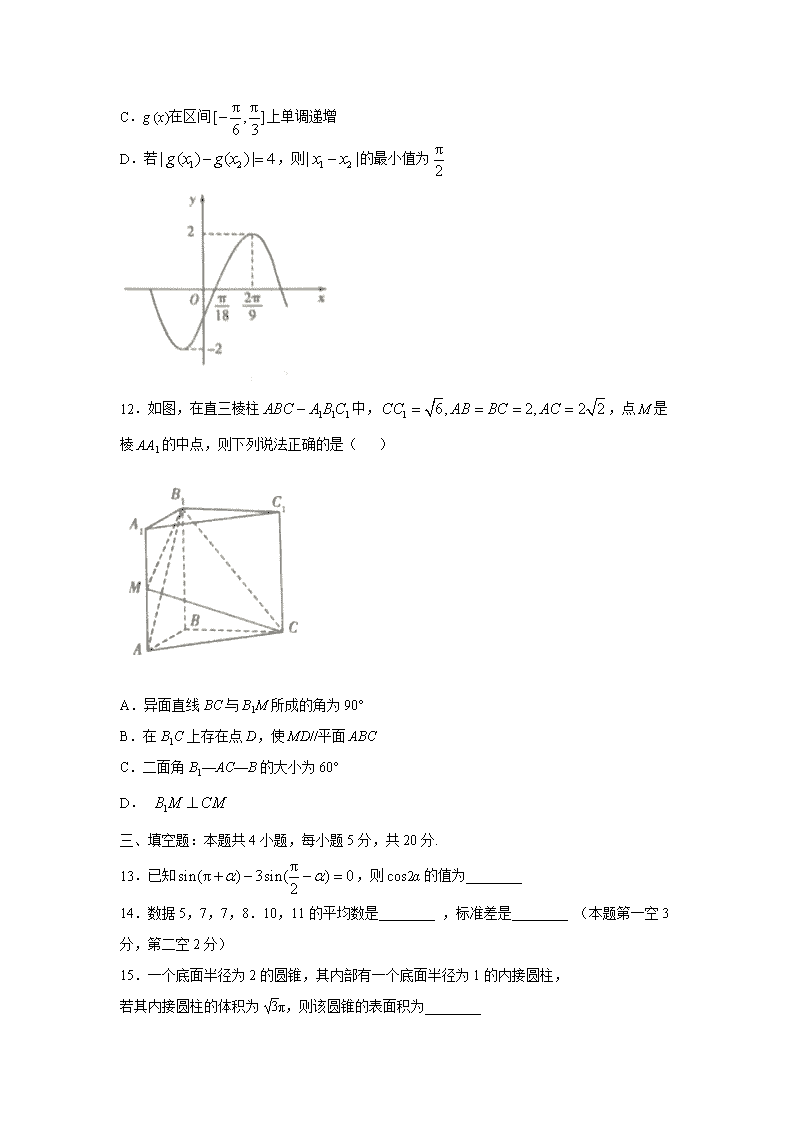
山东省临沂市2019-2020学年高一下学期期末考试数学试题 一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知复数z满足(i为虚数单位),则为z的共轭复数)在复平面内对应的点位于( ) A.第一限 B.第二象限 C.第三象限 D.第四象限 2.的值为( ) 3.某工厂12名工人的保底月薪如右表所示,第80百分位是( ) A. 3050 B. 2950 C. 3130 D. 3325 4.从两名男生和两名女生中任意抽取两人,若采取有放回简单随机抽样,则抽到的两人中有一男一女的概率是( ) 5.已知向量是两个非零向量,且,则夹角为( ) 6.已知α,β是两个不同的平面,m,n是两条不同的直线,下列四个命题中正确的是( ) A.如果m∥α,n∥α,那么 m∥n B.如果m⊥α,n∥α,,那么m⊥n C.如果m⊥n,m⊥α,n//β,那么α⊥β D.如果m//n,α∥β,么m与α所成的角和n与β所成的角不相等 7.魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成几何体为“牟合方盖”,刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为π :4,若“牟合方盖”的体积为18,则正方体的棱长为( ) A. 18 B.6 C.3 D. 2 8.在△ABC中,角A,B,C的对边分别为a,b,c,A=60°,且a=2b-c,则△ABC的形状为( ) A.钝角三角形 B.等腰直角三角形 C.直角三角形 D.等边三角形 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求的.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.设i为虚数单位,复数,则下列命题正确的是( ) A.若z为纯虚数,则实数a的值为2 B.若z在复平面内对应的点在第三象限,则实数a的取值范围是 C.实数是为z的共轭复数)的充要条件 D.若,则实数a的值为2 10.下列说法正确的是( ) A.在△ABC中,若,则点D是边BC的中点 B.已知,若,则x=-1 C.已知A,B,C三点不共线,B,C,M三点共线,若,则 D.已知正方形ABCD的边长为1,点M满足,则 11.已知函数的部分图象如图,将函数f(x)的图象所有点的横坐标伸长到原来的,再将所得函数图象向左平移个单位长度,得到函数g(x)的图象,则下列关于函数g(x)的说法正确的是( ) A.点是g(x)图象的一个对称中心 B. 是g(x)图象的一条对称轴 C.g (x)在区间上单调递增 D.若,则的最小值为 12.如图,在直三棱柱中,,点M是棱AA1的中点,则下列说法正确的是( ) A.异面直线BC与B1M所成的角为90° B.在B1C上存在点D,使MD//平面ABC C.二面角B1—AC—B的大小为60° D. 三、填空题:本题共4小题,每小题5分,共20分. 13.已知,则cos2α的值为________ 14.数据5,7,7,8.10,11的平均数是________ ,标准差是________ (本题第一空3分,第二空2分) 15.一个底面半径为2的圆锥,其内部有一个底面半径为1的内接圆柱, 若其内接圆柱的体积为π,则该圆锥的表面积为________ 16.如图,在四边形ABCD中,已知AB ⊥BC, AB=5,AD=7, ∠BCD=135°,,则 BC=________ 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17. (10分) 在平面直角坐标系xOy中,已知. (1)求与夹角的余弦值; (2)设,若BP⊥AC,求实数λ的值. 18. (12分) 某学校就学生对端午节文化习俗的了解情况,进行了一次20道题的问卷调查,每位同学都是独立答题,在回收的试卷中发现甲同学答对了12个,乙同学答对了16个.假设答对每道题都是等可能的,试求: (1)任选一道题日,甲乙都没有答对的概率; (2)任选一道题目,恰有一人答对的概率. 19. (12分) 在△ABC中,角A,B,C的对边分别为a,b,c,且. (1)求A; (2)在这三个条件中,选出两个使△ABC唯一确定的条件补充在下面的问题中,并解答问题,若________,________,求△ABC的面积.(注:如果选择多个条件分别解答,按第一个解答计分.) 20. (12分) 受突如其来的新冠疫情的影响,全国各地学校都推迟2020 年的春季开学,某学校“停课不停学",利用云课平台提供免费线上课程,该学校为了解学生对线上课程的满意程度,随机抽取了100名学生对该线上课程评分、其频率分布直方图如图. (1)求图中a的值; (2)求评分的中位数; (3)以频率当作概率,若采用分层抽样的方法,从样本评分在[60,70)和[90, 100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率. 21.(12分) 如图,在平行四边形ABCM中,AB=AC=4, ∠ACM=90°,以AC 为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA. (1)证明:平面ACD⊥平面ABC; (2)设Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积. 22. (12分) 已知,将曲线y=f(x)的图象向右平移 得到函数y=g(x)的图象. (1)若,求的值; (2)若不等式对任意x∈R恒成立,求实数m的取值范围. 【参考答案】查看更多