2020高中数学 课时分层作业10 双曲线及其标准方程 新人教A版选修2-1
课时分层作业(十) 双曲线及其标准方程
(建议用时:40分钟)
[基础达标练]
一、选择题
1.已知平面内两定点A(-5,0),B(5,0),动点M满足|MA|-|MB|=6,则点M的轨迹方程是( )
A.-=1 B.-=1(x≥4)
C.-=1 D.-=1(x≥3)
D [由题意知,轨迹应为以A(-5,0),B(5,0)为焦点的双曲线的右支.由c=5,a=3,知b2=16,
∴P点的轨迹方程为-=1(x≥3).]
2.若方程+=1,k∈R表示焦点在x轴上的双曲线,则k的取值范围是( )
【导学号:46342092】
A.-3
-2
D.k>-2
A [由题意知,解得-30,b>0),
则有a2+b2=c2=8,-=1,解得a2=3,b2=5.
故所求双曲线的标准方程为-=1.]
8.一动圆过定点A(-4,0),且与定圆B:(x-4)2+y2=16相外切,则动圆圆心的轨迹方程为________.
5
-=1(x≤-2) [设动圆圆心为P,由题意知|PB|=|PA|+4,即|PB|-|PA|=4<|AB|,则动圆圆心P的轨迹是以点A,B为焦点的双曲线的左支,又a=2,c=4,则b2=12,故动圆圆心的轨迹方程为-=1(x≤-2).]
三、解答题
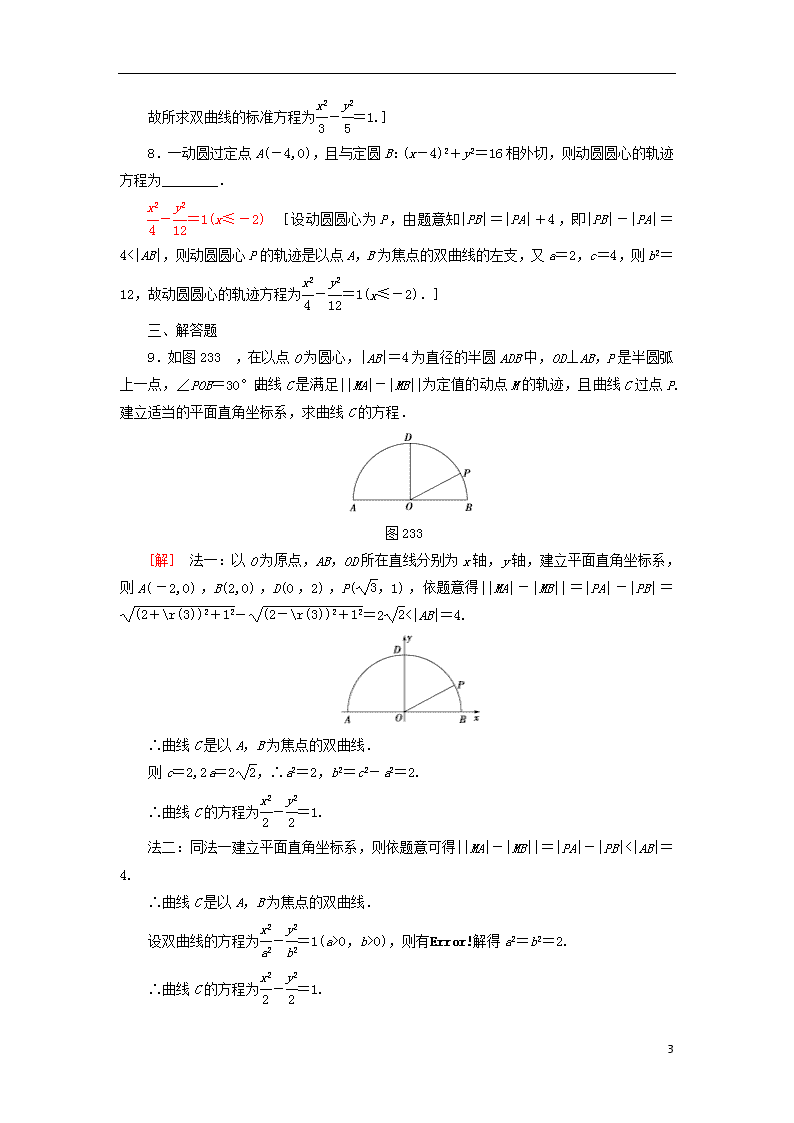
9.如图233,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.建立适当的平面直角坐标系,求曲线C的方程.
图233
[解] 法一:以O为原点,AB,OD所在直线分别为x轴,y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P(,1),依题意得||MA|-|MB||=|PA|-|PB|=-=2<|AB|=4.
∴曲线C是以A,B为焦点的双曲线.
则c=2,2a=2,∴a2=2,b2=c2-a2=2.
∴曲线C的方程为-=1.
法二:同法一建立平面直角坐标系,则依题意可得||MA|-|MB||=|PA|-|PB|<|AB|=4.
∴曲线C是以A,B为焦点的双曲线.
设双曲线的方程为-=1(a>0,b>0),则有解得a2=b2=2.
∴曲线C的方程为-=1.
10.已知方程kx2+y2=4,其中k为实数,对于不同范围的k值分别指出方程所表示的曲线类型.
【导学号:46342094】
[解] (1)当k=0时,y=±2,表示两条与x轴平行的直线;
(2)当k=1时,方程为x2+y2=4,表示圆心在原点,半径为2的圆;
5
(3)当k<0时,方程为-=1,表示焦点在y轴上的双曲线;
(4)当0<k<1时,方程为+=1,表示焦点在x轴上的椭圆;
(5)当k>1时,方程为+=1,表示焦点在y轴上的椭圆.
[能力提升练]
1.设θ∈,则关于x,y的方程+=1所表示的曲线是( )
A.焦点在y轴上的双曲线
B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆
D.焦点在x轴上的椭圆
B [由题意,知-=1,因为θ∈,所以sin θ>0,-cos θ>0,则方程表示焦点在x轴上的双曲线.故选B.]
2.已知P为双曲线-=1右支上一点,F1,F2分别为双曲线的左、右焦点,M为△PF1F2的内心,若S△PMF1=S△PMF2+8,则△MF1F2的面积为( )
A.2 B.10 C.8 D.6
B [设△PF1F2的内切圆的半径为R,由题意,知a=4,b=3,c=5.∵S=S+8,∴(|PF1|-|PF2|)R=8,即aR=8,∴R=2,∴S=·2c·R=10,故选B.]
3.已知双曲线-=1的左焦点为F,点P为双曲线右支上的一点,且PF与圆x2+y2=16相切于点N,M为线段PF的中点,O为坐标原点,则|MN|-|MO|=________.
【导学号:46342095】
-1 [设F′是双曲线的右焦点,连接PF′(图略),因为M,O分别是FP,FF′的中点,所以|MO|=|PF′|,又|FN|==5,由双曲线的定义知|PF|-|PF′|=8,故|MN|-|MO|=|MF|-|FN|-|PF′|=(|PF|-|PF′|)-|FN|=×8-5=-1.]
4.已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是________.
(-1,3) [由题意得(m2+n)(3m2-n)>0,解得-m2
查看更多