2019学年高一数学10月月考试题新人教版 新版

2019学年高一数学10月月考试题新人教版 新版

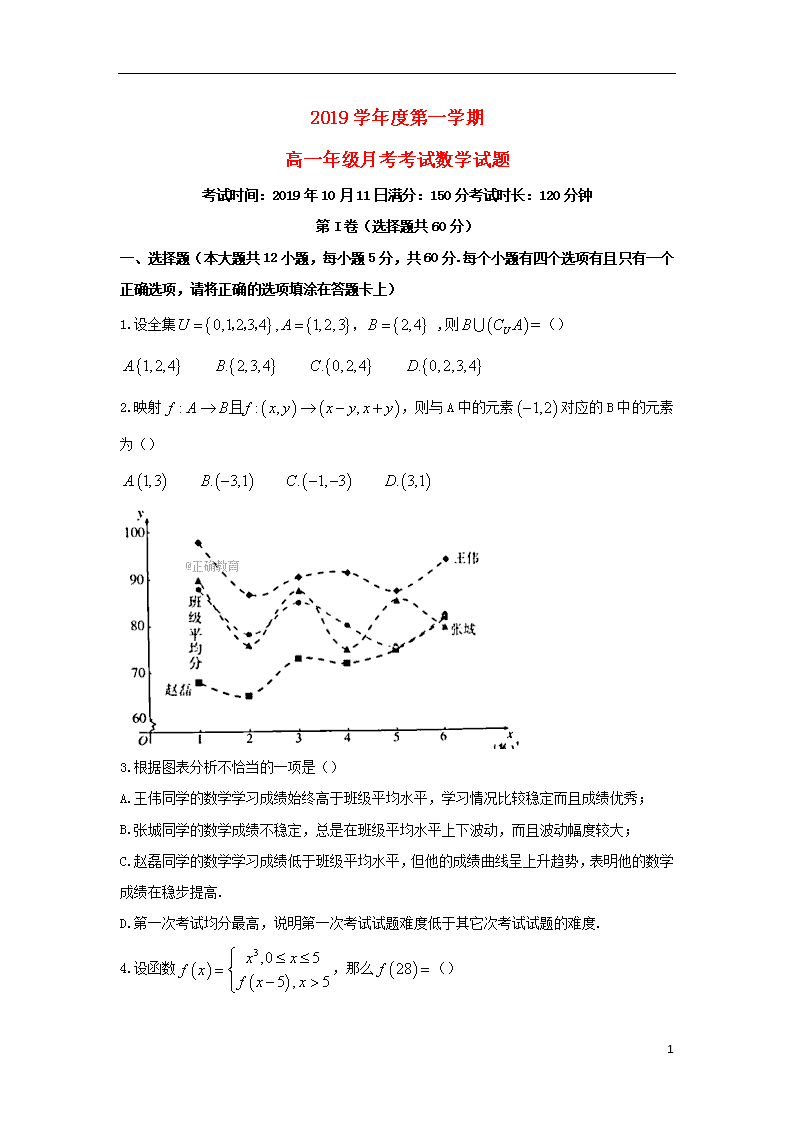
‎2019学年度第一学期 高一年级月考考试数学试题 考试时间：2019年10月11日满分：150分考试时长：120分钟 第I卷（选择题共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分.每个小题有四个选项有且只有一个正确选项，请将正确的选项填涂在答题卡上）‎ ‎1.设全集 ,则（）‎ ‎2.映射，则与A中的元素对应的B中的元素为（）‎ ‎3.根据图表分析不恰当的一项是（）‎ A.王伟同学的数学学习成绩始终高于班级平均水平，学习情况比较稳定而且成绩优秀；‎ B.张城同学的数学成绩不稳定，总是在班级平均水平上下波动，而且波动幅度较大；‎ C.赵磊同学的数学学习成绩低于班级平均水平，但他的成绩曲线呈上升趋势，表明他的数学成绩在稳步提高.‎ D.第一次考试均分最高，说明第一次考试试题难度低于其它次考试试题的难度.‎ ‎4.设函数，那么（）‎ 5‎ ‎5.下列函数中，不满足的是（）‎ ‎6.已知偶函数在上单调递减，则的大小关系是（）‎ ‎7.已知集合，则（）‎ ‎8.函数的值域是（）‎ ‎9. 设，若，则实数的取值范围是（）‎ ‎10.已知分别是定义在R上的偶函数和奇函数，且，则的值为（）‎ ‎11.已知函数在R上为单调递增函数，则实数的取值范围是（）‎ ‎12.对于任意两个正整数定义某种运算如下：当都为正偶数或正奇数时，‎ 5‎ ‎；当中一个为正偶数，另一个为正奇数时，，在此定义下，集合中的元素个数是（）‎ 第II卷（非选择题共90分）‎ 二、填空题（本大题共4个小题，每小题5分，共20分.请将正确答案填写在答题上）‎ ‎13.函数的定义域为____________‎ ‎14.函数在上是递增函数，则实数的取值范围__________‎ ‎15.已知定义在R上的奇函数，当，则函数的解析式______________‎ ‎16.给出下列四个命题：‎ ‎（1）若集合 ‎（2）若函数的定义域为，则函数的定义域为.‎ ‎（3）函数的单调递减区间是；‎ ‎（4）若，且，则 其中，正确的命题有___________（填序号）‎ 三、解答题（本大题共70分.解答应写出文字说明，证明过程或演算步骤）‎ ‎17.（本小题共10分）已知全集，‎ 求 ‎18.（本小题共12分）‎ 5‎ ‎《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过3500元的部分不必纳税，超过3500元的部分为全月应纳税所得额.此项税款按下表分段累计计算：‎ ‎（1）设应交纳税款为元，工资、薪金为元，写出与之间的函数关系式.‎ ‎（2）某人一月份应交纳税款为303元，那么他当月的工资、薪金所得是多少？‎ ‎19. （本小题共12分）已知集合，且，‎ 求的取值范围.‎ ‎20.（本小题共12分）已知函数 ‎（1）求的值；‎ ‎（2）用定义证明函数在区间上是减函数，说出在上的单调性.‎ ‎（3）若对任意的，总有成立，求实数m的取值范围.‎ ‎21.（本小题共12分）已知函数.‎ ‎（1）若函数具有单调性，求实数的取值范围；‎ 5‎ ‎（2）记函数的最小值为，求的解析式 ‎22.（本小题共12分）已知函数，当时，恒有 ‎（1）求证：为奇函数；‎ ‎（2）如果当时，恒有，证明函数在R上是单调递减；‎ ‎（3）在（2）条件下，解不等式.‎ 5‎