- 2021-07-01 发布 |
- 37.5 KB |
- 11页


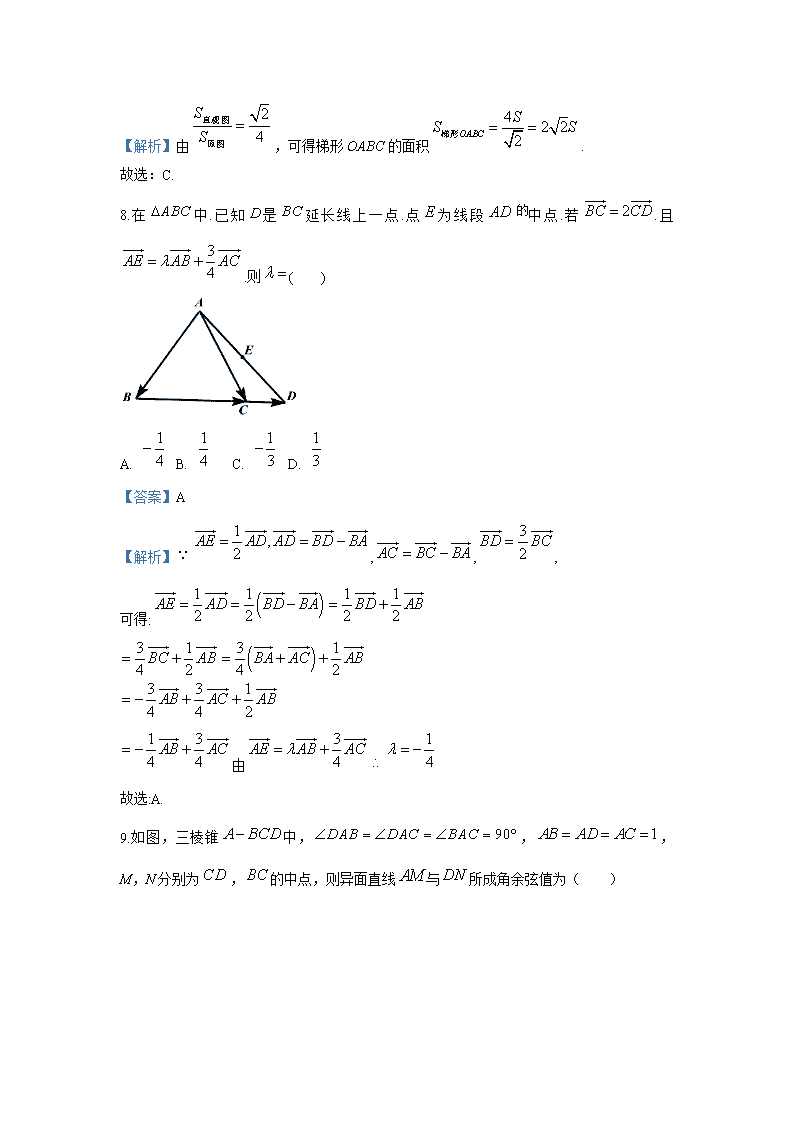
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】天津市宝坻区大钟庄高级中学2019-2020学年高一6月月考试题 (解析版)
天津市宝坻区大钟庄高级中学2019-2020学年高一6月月考数学试题 一、选择题(本大题共10小题,共50分) 1.已知复数z=(m2-m-6)+(m2+2m-8)i(i为虚数单位),若z<6,则实数m=( ) A. 2 B. 2或-4 C. 4 D. -2或4 【答案】A 【解析】因为z<6,故为实数,故,即,解得或. 当时成立;当时, 不满足.故. 故选:A 2.一个学校高一、高二、高三的学生人数之比为2:3:5,若用分层抽样的方法抽取容量为200的样本,则应从高三学生中抽取的人数为: A. 100 B. 80 C. 60 D. 40 【答案】A 【解析】由题意,学校高一、高二、高三的学生人数之比为2:3:5,采用分层抽样的方法抽取容量为200的样本,所以高三学生抽取的人数为人,故选A. 3.已知向量,,则( ) A. B. C. D. 【答案】B 【解析】由题意得,故选B. 4. 从甲、乙等5名学生中随机选出2人,则甲被选中的概率为( ) A. B. C. D. 【答案】B 【解析】从甲乙等名学生中随机选出人,基本事件的总数为,甲被选中包含的基本事件的个数,所以甲被选中的概率,故选B. 5.从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( ) A. “至少有一个黑球”与“都是黑球” B. “至少有一个黑球”与“至少有一个红球” C. “恰好有一个黑球”与“恰好有两个黑球” D. “至少有一个黑球”与“都是红球” 【答案】C 【解析】从装有两个红球和三个黑球的口袋里任取两个球, 在A中,“至少有一个黑球”与“都是黑球”能同时发生,不是互斥事件,故A错误; 在B中,“至少有一个黑球”与“至少有一个红球”能同时发生,不是互斥事件,故B错误; 在C中,“恰好有一个黑球”与“恰好有两个黑球”不能同时发生, 但能同时不发生,是互斥而不对立的两个事件,故C正确; 在D中,“至少有一个黑球”与“都是红球”是对立事件,故D错误. 故答案为:C 6.已知等边的边长为1,则( ) A. B. C. D. 【答案】D 【解析】解:因为三角形是等边三角形,边长为1,各内角为, 所以. 故选:D. 7.如图是一梯形OABC的直观图,其直观图面积为S,则梯形OABC的面积为( ) A. 2S B. S C. 2S D. S 【答案】C 【解析】由,可得梯形OABC的面积. 故选:C. 8.在中.已知是延长线上一点.点为线段中点.若.且.则( ) A. B. C. D. 【答案】A 【解析】,,, 可得: 由 故选:A. 9.如图,三棱锥中,,,M,N分别为,的中点,则异面直线与所成角余弦值为( ) A. B. C. D. 【答案】B 【解析】 取中点,连接,又因为为中点,故,故与所成角即为与所成的角.由题得,又为的中点, ,,所以,. 故,又. 又,故 所以异面直线与所成角余弦值为. 故选:B. 10.我国古代数学名著《九章算术》对立体几何也有深入研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱,其中,若,当“阳马”即四棱锥体积最大时,“堑堵”即三棱柱的表面积为 A. B. C. D. 【答案】C 【解析】详解:四棱锥的体积是三棱柱体积的,,当且仅当时,取等号. ∴. 故选C. 二、填空题(本大题共5小题,共20分) 11.计算复数_____________. 【答案】 【解析】解:. 故答案为:. 12.已知一组数据4.7,6.1,4.2,5.0,5.3,5.5,则该组数据的第25百分位数是________. 【答案】4.7 【解析】把这组数据按从小到大的顺序排列,可得:4.2,4.7,5.0,5.3,5.5,6.1共6个数据, 由 ,所以这组数据的第25百分位数是第2项,即4.7. 故答案为:4.7. 13.已知向量,,则向量的坐标是____________. 【答案】 【解析】 14.如图,点在正方形所在的平面外,,则与所成角的度数为____________. 【答案】 【解析】如图所示,以D为坐标原点,DA所在的直线为轴,DC所在的直线为轴,DP所在的直线为轴,建立空间直角坐标系, 因为点P在正方形ABCD所在平面外,平面, 令,所以, 所以, 所以,所以, 即异面直线PA与BD所成的角为 15.给出下列命题: ①如果a,b是两条直线,且a//b,那么a平行于经过b的任何平面; ②如果直线a和平面α满足a//α,那么直线a与平面α内的任何直线都平行; ③如果直线a,b和平面α满足a//α,b//α,那么a//b. 其中错误命题的序号是___________. 【答案】(1)(2)(3) 【解析】(1)如果a,b是两条直线,且a//b,那么a平行于经过b任何平面.不正确,a,b可能在同一个平面内; (2)如果直线a和平面α满足a//α,那么直线a与平面α内的任何直线都平行.不正确,直线a与平面α内的直线可能平行,也可能异面; (3)如果直线a,b和平面α满足a//α,b//α,那么a//b.不正确,a,b的位置关系为:平行、相交或异面. 故答案为:(1)(2)(3). 三、解答题(本大题共5小题,共50分) 16.在△ABC中,a=7,b=8,cosB= –. (Ⅰ)求∠A; (Ⅱ)求AC边上的高. 解:(1)在△ABC中,∵cosB=–,∴B∈(,π),∴sinB=.由正弦定理得 =,∴sinA=.∵B∈(,π),∴A∈(0,),∴∠A=. (2)在△ABC中,∵sinC=sin(A+B)=sinAcosB+sinBcosA==. 如图所示,在△ABC中,∵sinC=,∴h==,∴AC边上的高为. 17.设,,求的值. 解:∵,∴.又∵,∴. ∴,则. 18.掷红、白两颗骰子,事件A={红骰子点数小于3},事件B={白骰子点数小于3},求: (1)P(A∩B); (2)P(A∪B). 解:掷红、白两颗骰子,出现向上的点数如下表所示: 白1 白2 白3 白4 白5 白6 红1 (红1,白1) (红1,白2) (红1,白3) (红1,白4) (红1,白5) (红1,白6) 红2 (红2,白1) (红2,白2) (红2,白3) (红2,白4) (红2,白5) (红2,白6) 红3 (红3,白1) (红3,白2) (红3,白3) (红3,白4) (红3,白5) (红3,白6) 红4 (红4,白1) (红4,白2) (红4,白3) (红4,白4) (红4,白5) (红4,白6) 红5 (红5,白1) (红5,白2) (红5,白3) (红5,白4) (红5,白5) (红5,白6) 红6 (红6,白1) (红6,白2) (红6,白3) (红6,白4) (红6,白5) (红6,白6) 共有36种可能. (1)事件包含(红1,白1),(红1,白2),(红2,白1),(红2,白2)4种, . (2)事件包含(红1,白1),(红1,白2),(红1,白3),(红1,白4),(红1,白5),(红1,白6),(红2,白1),(红2,白2),(红2,白3),(红2,白4),(红2,白5),(红2,白6),(红3,白1),(红4,白1),(红5,白1),(红6,白1),(红3,白2),(红4,白2),(红5,白2),(红6,白2)共20种, . 19.如图所示,已知平面,,分别是,的中点,. (1)求证:平面; (2)求证:平面平面; (3)若,,求直线与平面所成的角. 解:(1)因为,分别是,的中点,所以. 又平面且平面,所以平面. (2)因为平面,平面,所以. 又且,所以平面. 又平面,所以平面平面. (3)因为平面,所以为直线与平面所成的角. 在直角中,,,所以.所以. 故直线与平面所成的角为. 20.有20名学生某次数学考试成绩(单位:分)的频率分布直方图如下: (1)求频率直方图中a的值; (2)分别求出成绩落在[50,60)与[60,70)中的学生人数; (3)试求本次考试数学平均成绩. 【答案】(1);(2)2,3;(3). 解:(1)由频率直方图可得. (2)成绩落在[50,60)中的学生人数为, 成绩落在[60,70)中的学生人数为. (3)本次考试数学的平均成绩为 .查看更多