初一数学试卷

初一数学试卷

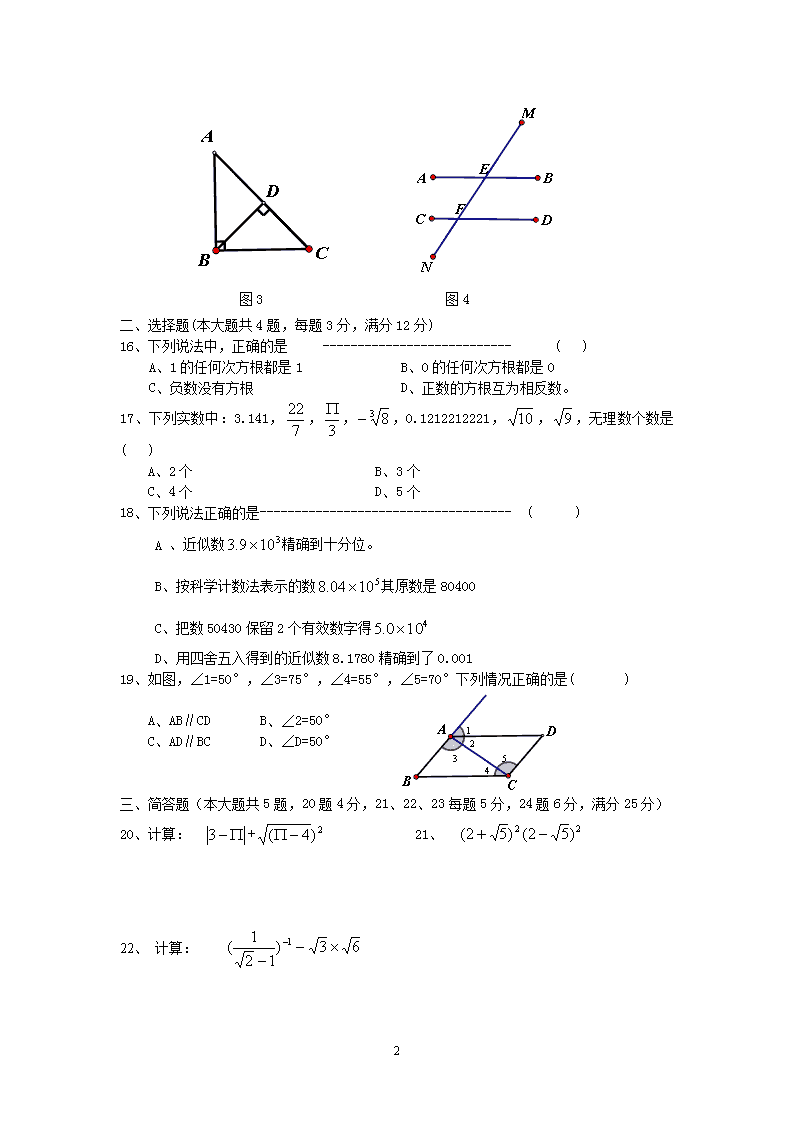
初一数学试卷 ‎（完卷时间90分钟，满分100分） ‎ 题 号 一 二 三 四 五 总分 得 分 一、 填空题（本大题共15题，每题2分，满分30分）‎ ‎1. 7的平方根是 , 是_________的平方根。‎ ‎2． 8的立方根是 。‎ ‎3. 的算术平方根是 。‎ ‎4. 把 表示成幂的形式是 。‎ ‎5. 在实数π、、- 、中，无理数是 。‎ ‎6. = ， =________________.‎ ‎7. 化简：‎ ‎8、若a、b是实数， 则___________.‎ ‎9. 精确到了________位，且有________个有效数字.‎ ‎10. 如果实数a在数轴上的对应点到原点的距离是，那么a= 。‎ ‎11．实数和在数轴对应的两点A、B之间的距离AB=________。‎ ‎12. 如图1，已知a∥b,∠1=(5t+10)°,∠2=(4t-10)°,则 t= 。‎ ‎13. 如图2，直线AB、CD、EF 相交与点O,∠AOE的角是_____________.‎ ‎ ‎ ‎ 图1 图2 ‎ ‎14. 如图3，点C到直线BD的距离就是线段 的长度 。‎ ‎15. 如图4，直线MN与直线AB、CD分别交于点E、F，要使AB∥CD，需要添加一个条件，这个条件可以是_____________________(只需写出一种情况)‎ 6‎ ‎ ‎ 图3 图4‎ 一、 选择题(本大题共4题，每题3分，满分12分)‎ ‎16、下列说法中，正确的是 --------------------------- ( )‎ A、1的任何次方根都是1 B、0的任何次方根都是0‎ C、负数没有方根 D、正数的方根互为相反数。‎ ‎17、下列实数中：3.141，，，，0.1212212221，，，无理数个数是 ( )‎ A、2个 B、3个 C、4个 D、5个 ‎18、下列说法正确的是------------------------------------ ( )‎ A 、近似数精确到十分位。‎ ‎ B、按科学计数法表示的数其原数是80400‎ ‎ C、把数50430保留2个有效数字得 ‎ D、用四舍五入得到的近似数8.1780精确到了0.001‎ ‎19、如图，∠1=50°，∠3=75°，∠4=55°，∠5=70°下列情况正确的是( )‎ A、AB∥CD B、∠2=50° ‎ ‎ C、AD∥BC D、∠D=50° ‎ 三、简答题（本大题共5题，20题4分，21、22、23每题5分，24题6分，满分25分）‎ ‎20、计算： + 21、 ‎ ‎22、 计算： ‎ 6‎ ‎23．利用幂的性质进行计算： ‎ ‎24、计算： ‎ 四、填写理由（每题7分，满分１４分）‎ ‎25、如图，在 △ABC中，FG∥EB,∠2=∠3,那么∠EDB+∠DBC等于多少度？为什么？‎ 解（1）∠EDB+∠DBC=______________.‎ ‎ (2 ) 因为 FG∥EB ( )‎ ‎ 所以∠1=∠2 ( )‎ ‎ 因为∠2=∠3( 已知 )‎ ‎ 所以∠1=∠3( )‎ ‎ 所以 DE∥BC ( ) ‎ ‎ 所以∠EDB+∠DBC=______________.（ ）‎ ‎ ‎ ‎26如图：∠1与∠2互补，∠3=∠4 . 求证ＡＢ∥ＣＤ 证明　：∵　∠1与∠2互补　（已知）‎ ‎　　　　∴　∠1＋∠2＝１８０°（　　　　　　　　）‎ ‎　　　　∴　＿＿＿∥＿＿＿＿　　（　　　　　　　　　　　）‎ ‎　　　　∵　∠3=∠4　　（已知）‎ ‎∴　＿＿＿∥＿＿＿＿　　（　　　　　　　　　　　）‎ ‎∴　＿＿＿∥＿＿＿＿　　（　　　　　　　　　　　）‎ 五、画图题 （6分）‎ 6‎ ‎ 1、过点P作已知直线a的平行线b 。‎ ‎ 2、过P点作已知直线a的垂线c,垂足记作O 。‎ ‎ 3、点P与直线a的距离是线段_________的长度。‎ 六、综合题（本大题共2题，1题6分，2题7分，满分13分）‎ ‎1、如图，已知BF∥ED, AB∥CD, ∠B=50°,求∠D的度数。‎ 解 ：设 AB与DE交于点O.‎ ‎ 因为 BF∥ED (已知)‎ ‎ 所以∠AOE=∠B ( ) ‎ ‎ (以下由同学自行完成) ‎ ‎ ‎ ‎2、如图 已知∠A=∠D，∠C=∠F ,那么CE与BF平行吗？为什么？‎ 初一数学试卷参考答案以及评分建议 6‎ ‎（说明：下列解答中如果有不同的计算方法，请参照给分；若有不妥请自行纠正，谢谢！）‎ 一、 填空题（本大题共15题，每题2分，满分30分）‎ ‎（1）, 3 （2）2 （3） （4） （5） ‎ ‎（6）6， （7） （8）2 （9）十 ，3 （10）‎ ‎（11） （12）20 （13）∠FOB （14）CD (15) ∠MEB=∠MFD（答案不唯一）‎ 二、选择题(本大题共4题，每题3分，满分12分)‎ ‎（16）B （17）B （18）C （19）C 三、简答题（本大题共5题，20题4分，21、22、23每题5分，24题6分，满分25分）‎ ‎20、计算： + ‎ ‎ =()+()……………………………………………………2‎ ‎ =+ ………………………………………………………1‎ ‎ =1…………………………………………………………………………….1‎ ‎21、 ‎ ‎ =…………………………………………………………2‎ ‎ =(4-5)……………………………………………………………………………1‎ ‎ =(-1)……………………………………………………………………………1‎ ‎ =1…………………………………………………………………………………1‎ ‎22、 计算： ‎ ‎ =……………………………………………………..2‎ ‎ =…………………………………………………………2‎ ‎ =……………………………………………………………1‎ ‎23．利用幂的性质进行计算： ‎ ‎ =……………………………………………2‎ ‎ =…………………………………………..1‎ ‎ =………………………………………………1‎ ‎ =……………………………………………………1‎ 6‎ ‎24、计算： ‎ ‎ =…………………………………….4‎ ‎ =…………………………………………………..1‎ ‎ =………………………………………………………..1‎ 一、 填写理由（每题7分，满分１４分）‎ ‎25、（1）180°……………………………………………………1‎ ‎（2）已知，……………………………………………………1‎ 两直线平行 同位角相等，……………………………………………………1‎ ‎ ‎ ‎ 等量代换，……………………………………………………1‎ 内错角相等 两直线平行……………………………………………………1‎ ‎180°两直线平行 同旁内角互补……………………………………………………2‎ ‎26、补角的意义 ……………………………………………………1‎ ‎ EF∥CD (同旁内角互补,两直线平行) ……………………………………………………2‎ AB∥EF(同位角相等,两直线平行) ……………………………………………………2‎ CD∥AB(平行的传递性) ……………………………………………………2‎ 五、画图题（略）‎ 六、综合题（本大题共2题，1题6分，2题7分，满分13分）‎ ‎1、( 两直线平行,同位角相等 )‎ ‎ ∵　AB∥CD　（已知）　　‎ ‎　∴　∠AOE=∠D（　两直线平行 同位角相等）‎ ‎∴　∠B=∠D　　（等量代换）‎ ‎∵∠B=50°　　（已知）　　‎ ‎　∴　∠D=50°‎ ‎2 解 因为∠A=∠D （已知）‎ ‎ 所以 AC∥DF （内错角相等，两直线平行）‎ ‎ 得 ∠F=∠FBA （两直线平行，内错角相等）‎ ‎ 因为 ∠C=∠F （已知）‎ ‎ 得 ∠FBA =∠C （等量代换）‎ ‎ 所以 CE∥BF (同位角相等,两直线平行)‎ 6‎