浙江省绍兴市嵊州市2020届高三上学期期末考试数学试题 Word版含解析

浙江省绍兴市嵊州市2020届高三上学期期末考试数学试题 Word版含解析

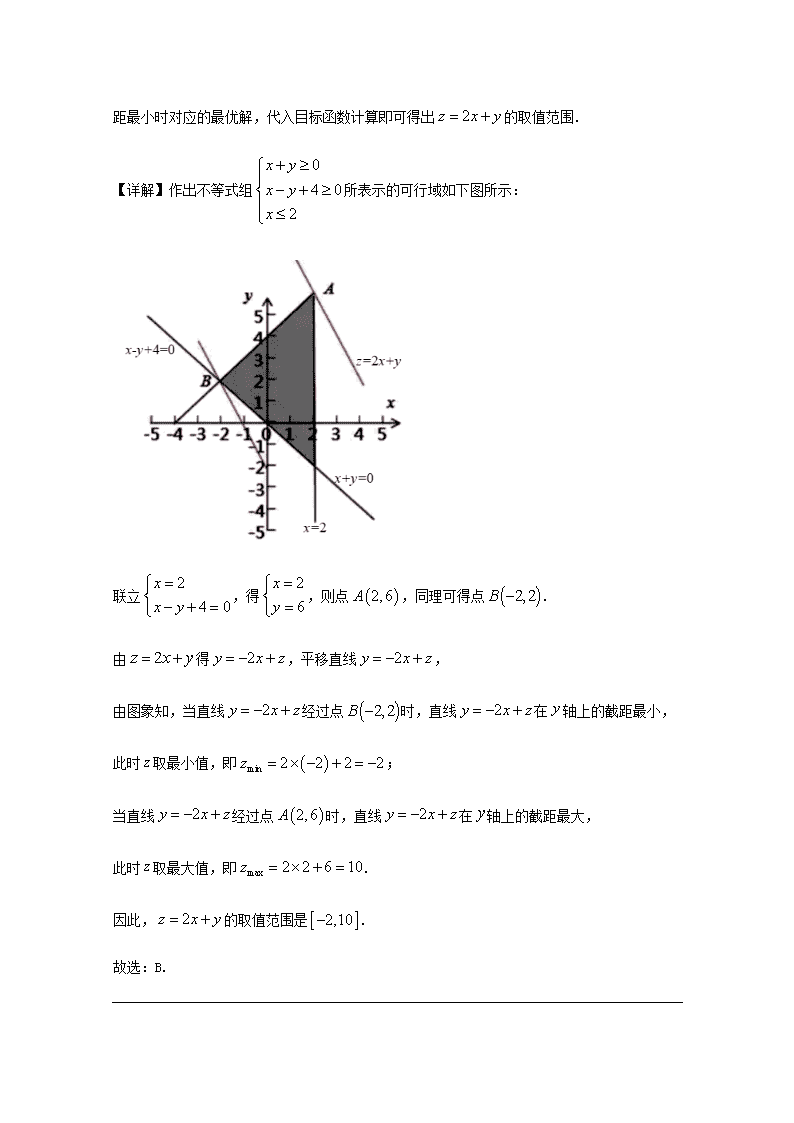
嵊州市 2019 学年第一学期期末教学质量调测 高三数学试题 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1.已知全集 ，集合 ，集合 ，则 （　　） A. B. C. D. 【答案】C 【解析】 【分析】 利用补集的定义可得出 ，再利用交集的定义可得出集合 . 【详解】由已知条件得 ，因此， . 故选：C. 【点睛】本题考查补集和交集的混合运算，考查计算能力，属于基础题. 2.若实数 、 满足约束条件 ，则 的取值范围是（　　） A. B. C. D. 【答案】B 【解析】 【分析】 作出不等式组对应的可行域，利用平移直线的方法找出直线 在 轴上截距最大和截 { }1,2,3,4,5U = { }1,2,3A = { }2,4B = ( )U A B = ∅ { }2 { }4 { }2,4 U A ( )U A B∩ { }4,5U A = ( ) { }4U A B∩ = x y 0 4 0 2 x y x y x + ≥  − + ≥  ≤ 2z x y= + [ ]2,4− [ ]2,10− [ ]2,4 [ ]2,10 2z x y= + y 距最小时对应的最优解，代入目标函数计算即可得出 的取值范围. 【详解】作出不等式组 所表示的可行域如下图所示： 联立 ，得 ，则点 ，同理可得点 . 由 得 ，平移直线 ， 由图象知，当直线 经过点 时，直线 在 轴上的截距最小， 此时 取最小值，即 ； 当直线 经过点 时，直线 在 轴上的截距最大， 此时 取最大值，即 . 因此， 的取值范围是 . 故选：B. 2z x y= + 0 4 0 2 x y x y x + ≥  − + ≥  ≤ 2 4 0 x x y =  − + = 2 6 x y =  = ( )2,6A ( )2,2B − 2z x y= + 2y x z= − + 2y x z= − + 2y x z= − + ( )2,2B − 2y x z= − + y z ( )min 2 2 2 2z = × − + = − 2y x z= − + ( )2,6A 2y x z= − + y z max 2 2 6 10z = × + = 2z x y= + [ ]2,10− 【点睛】本题主要考查线性规划的基本应用，利用目标函数的几何意义找出最优解是解决问 题的关键，考查数形结合思想的应用，属于基础题. 3.已知复数 ， （其中 是虚数单位），则 （　　） A. B. C. D. 【答案】B 【解析】 【分析】 利用复数的除法运算法则化简计算即可. 【详解】由已知条件得 . 故选：B. 【点睛】本题考查复数的除法运算，考查计算能力，属于基础题. 4.函数 的图象大致是（　　） A. B. C. D. 【答案】C 【解析】 3z i= − 2 1z i= + i 1 2 z z = 2 2i− 1 2i− 1 i+ 2 i+ ( )( ) ( )( )1 2 3 13 2 4 1 21 1 1 2 i iz i i iz i i i − −− −= = = = −+ + − ( ) 2 2 2 1x x xf x −= + 【分析】 求解函数 的零点，考查函数 在 时的函数值符号，可得出结论. 【详解】由 ，得 ，解得 或 ，该函数有两个零点，有一个正 零点，排除 A、B 选项； 当 时， ，排除 D 选项. 故选：C. 【点睛】本题考查函数图象的识别，一般分析函数的定义域、奇偶性、单调性、零点以及函 数值符号，结合排除法得出选项，考查推理能力，属于中等题. 5.已知 ，则“ ”是“ ”成立的（　　）条件 A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要 【答案】B 【解析】 【分析】 求出不等式 在 上的解，然后利用集合的包含关系即可得出结论. 【详解】 ，解不等式 ，得 ，  ，因此，“ ”是“ ”成立的必要不充分条件. 故选：B. 【点睛】本题考查必要不充分条件的判断，涉及正弦不等式的求解，考查推理能力与运算求 解能力，属于中等题. ( )y f x= ( )y f x= ( )0,2x∈ ( ) 0f x = 2 2 0x x− = 0x = 2x = 0 2x< < ( ) 2 2 02 1x x xf x −= <+ ( )0,x π∈ 6x π> 1sin 2x > 1sin 2x > ( )0,x π∈ ( )0,x π∈ 1sin 2x > 5 6 6x π π< < 5,6 6 π π     ,6 π π     6x π> 1sin 2x > 6.若圆 上的点到直线 的最大距离与最小距离的差为 ，则实数 的值是（　　） A. B. C. D. 【答案】D 【解析】 【分析】 先将圆的方程化为标准方程，设圆心到直线的距离 ，则圆 上的点 到直线 的最大距离为 ，最小距离为 （ 为圆的半径），根据已知条 件求出半径，从而可求得 的值. 【详解】圆的方程化为标准方程得 ，则 ， 圆的半径为 ，设圆心 到直线 的距离为 ， 当 时，圆 上 点到直线 的最大距离为 ， 最小距离为 ，由已知条件得 ， 即 ，解得 . 此时， ，直线 与圆 相离，合乎题意. 当 时，圆 上的点到直线 的最大距离为 ，最 小距离为 ，由已知条件得 ，舍去 综上， 故选：D. 的 2 2 2 2 0x y x y k+ − − − = 10 0x y+ − = 6 k 34− 1 4 7 d 2 2 2 2 0x y x y k+ − − − = 10 0x y+ − = d r+ d r− r k ( ) ( )2 21 1 2x y k− + − = + 2 0 2k k+ > ⇒ > − 2r k= + ( )1,1 10 0x y+ − = d 8 4 2 2 d = = d r> 2 2 2 2 0x y x y k+ − − − = 10 0x y+ − = d r+ d r− ( ) ( ) 2 6 3d r d r r r+ − − = = ⇒ = 2 3k + = 7k = 8 4 2 3 2 d = = > 10 0x y+ − = ( ) ( )2 21 1 9x y− + − = d r≤ 2 2 2 2 0x y x y k+ − − − = 10 0x y+ − = d r+ 0 6 6 4 2 4 2d r r+ = ⇒ = − < 7k = 【点睛】本题考查了圆上的点到直线距离的最大值和最小值的求解，考查运算求解能力，属 于中等题. 7.设 ，随机变量 的分布列是 则当 在 内变化时，（　　） A. 增大 B. 减小 C. 先增大后减小 D. 先减小后增大 【答案】A 【解析】 【分析】 计算出 和 ，根据 将 表示成关于 的函数，研究 函数的单调性即可得出结论. 【详解】 ， 由分布列得 ， ， 0 1p< < ξ ξ 1− 0 1 P 1 2 1 2 p− 2 p p ( )0,1 ( )D ξ ( )D ξ ( )D ξ ( )D ξ ( )E ξ ( )2E ξ ( ) ( ) ( )2 2D E Eξ ξ ξ= − ( )D ξ p ( ) ( ) ( ) ( )2 2 2 1 1 2 n n i i i i i i i D E p E E pξ ξ ξ ξ ξ ξ ξ = =  = − ⋅ = − + ⋅    ∑ ∑ ( ) ( ) ( ) ( ) ( ) ( ) ( )2 2 2 2 2 2 2 1 2 2 n i i i i i p p E E E E E E Eξ ξ ξ ξ ξ ξ ξ ξ ξ =  = − + = − + = − ∑ ( ) 1 1 11 0 12 2 2 2 p p pE ξ − −= − × + × + × = ( )2 1 1 11 02 2 2 p p pE ξ + − += × + × = 所以， ， 所以，当 时， 随着 的增大而增大. 故选：A. 【点睛】本题考查离散型随机变量的期望和方差，考查二次函数的单调性，属于中等题. 8.如图，在三棱锥 中，已知 平面 ， ，且 ，设 是棱 上的点（不含端点）．记 ， ，二面角 的大小 为 ，则（　　） A. ，且 B. ，且 C. ，且 D. ，且 【答案】D 【解析】 【分析】 作出二面角 的平面角，利用角的余弦值的大小关系得出 与 、 与 的大小 关系. ( ) ( ) ( ) ( )2 22 2 21 1 1 1 1 522 2 4 4 4 4 p pD E E p p pξ ξ ξ + − = − = − = − + + = − − +   ( )0,1p∈ ( )D ξ p D ABC− DA ⊥ ABC AB BC⊥ DA AB BC= = P DC PAB α∠ = PBC β∠ = P AB C- - γ γ α> γ β> γ α> γ β< γ α< γ β> γ α< γ β< P AB C- - γ α γ β 【详解】如下图所示： 过点 作 交 于点 ，过点 作 交 于点 ，过点 作 交 于点 ，连接 、 、 . ， 平面 ， 平面 ， 平面 ， ， ， ， ， ， 平面 ， 同理可得 平面 ， 平面 ， ， ， 易知 ， ， ， ，则 ， ， ， . ， ， ，则四边形 为矩形， ， 则 ， . 综上所述， ，且 . 故选：D. P //PO AD AC O O //OE BC AB E O //OF AB BC F OB PE PF //PO AD AD ⊥ ABC PO∴ ⊥ ABC AB ⊂ ABC AB PO∴ ⊥ //OE BC BC AB⊥ OE AB∴ ⊥ OE PO O=  AB∴ ⊥ POE BC ⊥ POF PE ⊂ POE AB PE∴ ⊥ PEO γ∴∠ = PE PA< PE PB< AB BC= AB BC⊥ 45BAC∠ =  OE AE∴ = cos cosAE OE PA PE α γ= < = γ α∴ < //OE BF OF //BE 90EBF∠ =  OEBF OE BF∴ = cos cosOE BF PE PB γ β= > = γ β∴ < γ α< γ β< 【点睛】本题考查二面角与线线角的大小比较，作出二面角的平面角，并利用三角函数值的 大小关系来得出角的大小关系是解题的关键，考查化归与转化思想的应用，属于中等题. 9.已知 、 ，设函数 ，若函数 有且只有一个零点，则 （　　） A. ，且 B. ，且 C. ，且 D. ，且 【答案】D 【解析】 【分析】 令 ，可知关于 的二次方程 有实根，可得出 ，分 与 两种情况讨论，先求出方程 的根，再讨论函数 的零点 即可得出结论. 【详解】设 ，则关于 的二次方程 有根，可得出 ， 解得 . ①当 时， ，解方程 ，得 ， 此时方程 只有一根，即 只有一根，则 ； ②当 时， ， 解方程 ，得 ， ，则 ， a b R∈ ( ) 2f x x ax b= + + ( )( )y f f x= 0a ≤ 0b ≤ 0a ≤ 0b ≥ 0a ≥ 0b ≤ 0a ≥ 0b ≥ ( )u f x= u 2 0u au b+ + = 2 4 0a b∆ = − ≥ 0∆ = > 0∆ 2 0u au b+ + = ( )u f x= ( )u f x= u 2 0u au b+ + = 2 4 0a b∆ = − ≥ 2 4 2 a b acu − ± −= 2 4 0a b∆ = − = 2 4 ab = 2 2 04 au au+ + = 2 au = − ( ) 2 af x = − 2 2 2 a ax + = −   0 02 a a b− = ⇒ = = 2 4 0a b∆ = − > 2 4 ab < 2 0u au b+ + = 2 1 4 2 a a bu − + −= 2 2 4 2 a a bu − − −= 1 2u u> 则方程 只有一解，方程 无实解， 所以， ，化简得 ， 综上所述， 且 . 故选：D. 【点睛】本题考查了复合型二次函数的零点问题，一般将复合函数分解为内层函数与外层函 数来分析，考查分析问题和解决问题的能力，属于难题. 10.已知数列 满足 ， ，若 ，则（　　） A. B. C. D. 【答案】C 【解析】 【分析】 由递推公式 得出 ，计算出 ，利用递推公式推导得出 （ 为正奇数）， （ 为正偶数），利用定义判断出数列 和 的单调性，进而可得出结论. 【详解】 ， ， ( ) 1f x u= ( ) 2f x u= ( ) 2 2 min 4 4 4 2 b a a a bf x − − + −= = 2 24 4 02 a ba a b −= + − > 2 2 24 0 4 , 04 2 a a a bb a b a b − + −< ∴ < ∴ − < ∴ > 0a ≥ 0b ≥ { }na 1 2 2 1 n n n aa a+ += + n ∗∈N 1 10 2a< < 8 9 72a a a+ < 9 10 82a a a+ > 6 9 7 8a a a a+ > + 7 10 8 9a a a a+ > + 1 2 2 1 n n n aa a+ += + 2 5 4 4 5 n n n aa a+ += + 2 5 ,24a  ∈   ( )0,1na ∈ n 1na > n { }( )2 1na n N ∗ − ∈ { }( )2na n N ∗∈ ( ) ( )1 1 32 12 1 32 2 2 1 2 1 2 2 2 1 n n n n n n aaa a a a+ + ++= = = ++ + + 1 10, 2a  ∈   2 5 ,24a  ∴ ∈   ， ， 且 ， . ，则 ，则 ， 如此继续可得知 ，则 ， 所以，数列 单调递增； 同理可知， ，数列 单调递减. 对于 A 选项， 且 ， ，A 选项错误； 对于 B 选项， 且 ，则 ，B 选项错误； 对于 C 选项， ， ，则 ，C 选项正确； 对于 D 选项， ， ，则 ，D 选项错误. 故选：C. 【点睛】本题考查数列不等式的判断，涉及数列递推公式的应用，解题的关键就是推导出数 列 和 的单调性，考查推理能力，属于难题. 二、填空题：本大题共 7 小题，多空题每小题 6 分，单空题每小题 6 分，共 36 分． 11.若直线 与直线 平行，则 _____， 与 之间的距离是____． ( ) ( )1 2 1 2 5 92 4 52 2 1 5 4 5 94 4 22 1 4 5 4 5 4 4 4 52 12 1 n n n n n n nn n n n n a aa a aa aa a a a a + + + + + + −+ + += = = = = −++ + + +× ++ ( )2 2 4 15 4 4 5 4 5 nn n n n n n aaa a aa a+ −+− = − =+ + ( )2 1 2 12 2 1 2 1 nn n n n n n aaa a aa a+ −+− = − =+ + 1 10, 2a  ∈   10 1a< < ( ) ( )3 5 9 0,14 4 4 5n a a = − ∈+ ( )( )2 1 0,1na n N ∗ − ∈ ∈ ( )2 2 1 2 1 2 1 2 1 4 1 = 04 5 n n n n a a a a − + − − − − >+ { }( )2 1na n N ∗ − ∈ ( )2 1na n N ∗> ∈ { }( )2na n N ∗∈ 7 8a a< 7 9a a< 8 9 72a a a∴ + > 8 9a a> 10 8a a< 9 10 82a a a+ < 6 8a a> 9 7a a> 6 9 7 8a a a a+ > + 7 9a a< 10 8a a< 7 10 9 8a a a a+ < + { }( )2 1na n N ∗ − ∈ { }( )2na n N ∗∈ 1 :l y kx= 2 : 2 0l x y− + = k = 1l 2l 【答案】 (1). (2). 【解析】 【分析】 利用两直线平行的等价条件可求出实数 的值，利用平行线间的距离公式可求得直线 与 之 间的距离. 【详解】 ，且直线 的斜率为 ， ，则直线 的一般方程为 . 所以，直线 与 之间的距离是 . 故答案为： ； . 【点睛】本题考查利用两直线平行求参数，同时也考查了平行线间距离的求法，考查运算求 解能力，属于基础题. 12.学校开设了 门选修课，要求每一个学生从中任意选择 门，共有____种不同选法． 【答案】 【解析】 【分析】 利用组合计数原理可得出结果. 【详解】学校开设了 门选修课，要求每一个学生从中任意选择 门，共有 种不同的 选法. 故答案为： . 【点睛】本题考查组合数公式的应用，考查计算能力，属于基础题. 13.在《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的 三视图如图所示，俯视图中虚线恰好平分矩形的面积，则该“堑堵”的正视图的面积是_____ 1 2 k 1l 2l 1 2//l l 2l 1 1k∴ = 1l 0x y− = 1l 2l ( )22 2 2 1 1 = + − 1 2 7 3 35 7 3 3 7 35C = 35 ，体积是_____． 【答案】 (1). (2). 【解析】 【分析】 首先根据三视图作出几何体的直观图，结合三视图中的数据计算出正视图的面积和几何体的 体积. 【详解】由三视图可知，该几何体的直观图如下图所示： 该几何体为直三棱柱，正视图为等腰直角三角形，且斜边长上的高为 ，斜边长为 ， 故该“堑堵”的正视图的面积是 ，体积为 . 故答案为： ； . 【点睛】本题考查的主要知识点：三视图和几何体之间的转换，几何体体积公式的应用，主 要考查学生的运算能力以及空间想象能力，属于基础题. 1 2 1 2 1 2 1 12 × × = 1 2 2V = × = 1 2 14. 展开式中，各二项式系数的最大值是_____，常数项是____． 【答案】 (1). (2). 【解析】 【分析】 利用二项式系数的增减性可得出二项式系数的最大值，求出该二项展开式的通项 ，令 的 指数为零，求得 的值，代入通项即可得出常数项的值. 【详解】由题意可知， 展开式中，各二项式系数的最大值是 ， 展开式通项为 ，令 ，得 . 因此，展开式中的常数项为 . 故答案 ： ； . 【点睛】本题主要考查二项式定理的应用，考查了二项式系数的单调性以及展开式中常数项 的求解，考查运算求解能力，属于基础题. 15.在锐角 中， 是边 上一点，且 ， ， ，若 ，则 ____， 的面积是____． 【答案】 (1). (2). 【解析】 【分析】 先利用已知条件求出 ，利用二倍角公式可求出 的值， 再利用正弦定理求出 ，结合三角形的内角和以及诱导公式求出 ，利用三角形 为 61x x  −   20 15 1rT + x r 61x x  −   3 6 20C = ( ) 366 2 1 6 6 1 1 r rrr r r rT C x C x x −− +  = ⋅ ⋅ − = ⋅ − ⋅   36 02 r− = 4r = ( )44 6 1 15C ⋅ − = 20 15 ABC∆ D BC 2 2AB = 3BC = AC AD= 3cos 5CAD∠ = sinC = ABC∆ 2 5 5 3 ( ) 3cos2 cos 5C CADπ= − ∠ = − sinC sin BAC∠ sin B 的面积公式可求出 的面积. 【详解】如下图所示： 在锐角 中， 是边 上一点，且 ， ， ， ，即 ， ， ，又 ，解得 . 易知 为锐角，则 ， 由 ， . ， 因此， 的面积为 . 故答案为： ； . 【点睛】本题主要考查利用正弦定理解三角形以及三角形面积的计算，涉及二倍角公式的应 用，考查计算能力，属于中等题. ABC∆ ABC∆ D BC 2 2AB = 3BC = AC AD= ( ) 3cos 2 cos 5C CADπ − = ∠ = 3cos2 5C− = 3cos2 5C∴ = − 2 31 2sin 5C∴ − = − sin 0C > 2 5sin 5C = C 2 5cos 1 sin 5C C= − = 2 53sin 3 105sinsin sin 102 2 AB BC BC CBACC BAC AB × = ⇒ ∠ = = =∠ 2 10cos 1 sin 10BAC BAC∴ ∠ = − ∠ = ( ) 2sin sin sin cos cos sin 2B C BAC C BAC C BAC∴ = + ∠ = ∠ + ∠ = ABC∆ 1 1 2sin 2 2 3 32 2 2ABCS AB BC B∆ = ⋅ ⋅ = × × × = 2 5 5 3 16.已知单位向量 、 满足 ，设向量 ， ，则 的取值范围是_____． 【答案】 【解析】 【分析】 由 平方计算出 的值，然后将 转化为关于 的二次函数，利用二次函 数的基本性质可求得 的取值范围. 【详解】 单位向量 、 满足 ，即 ，整理得 ， 得 . ， 则 ， 设 ，该二次函数图象开口向上，对称轴为直线 ， 所以，函数 在 上单调递减，在 上单调递增， 当 时， ，即 ， 因此， 的取值范围是 . 故答案为： . 【点睛】本题考查向量模的取值范围的计算，考查了利用向量的模来计算数量积，将向量模 a b 2 2a b b− =   ( )2c a x b a= + −    [ ]0,1x∈ c a+  15 , 62       2 2a b b− =   a b⋅  2 c a+  x c a+   a b 2 2a b b− =   ( )2 2 2 4a b b− =   2 4 0a a b− ⋅ =   1 4a b⋅ =  ( ) ( )2 2 2 2c a a x b a x a xb+ = + − = − +       ( ) ( ) ( ) ( )22 2 2 2 22 2 2 4 2 4 4 2 4c a c a x a xb x x x a b x x x + = + = − + = − + − ⋅ + = − +         24 2 4y x x= − + 1 4x = 24 2 4y x x= − + 10, 4     1 ,14      [ ]0,1x∈ 15 64 y≤ ≤ 215 64 c a≤ + ≤  c a+  15 , 62       15 , 62       的取值范围转化为二次函数的值域来求解是解答的关键，考查运算求解能力，属于中等题. 17.已知函数 ，若对任意的实数 有 成立， 则实数 的取值范围是______. 【答案】 【解析】 【分析】 利用绝对值三角不等式得出 ，根据题意得出 ，解不等式即可 得出实数 的取值范围. 【详解】 ，则 ， 由绝对值三角不等式得 ， 则 ，由题意得 ，解得 . 故答案为： . 【点睛】本题考查函数不等式恒成立问题的求解，考查绝对值三角不等式的应用，属于中等 题. 三、解答题：本大题共 5 小题，共 74 分．解答应写出文字说明，证明过程或演算步骤． 18.已知函数 ． （1）求 的最小正周期； （2）当 时，求 的值域． ( ) 2 1f x x x= − − x ( ) ( ) ( )1f x t f x t R+ − ≤ ∈ t 1 1,3 3  −   ( ) ( ) max 3f x t f x t+ − = 3 1t ≤ t ( ) 2 1f x x x= − − ( ) ( ) ( ) ( )2 1 1f x t f x x t x x x t+ − = + − + − − + − ( ) ( ) ( ) ( )2 1 1 3f x t f x x t x x x t t+ − ≤ + − + − − + − = ( ) ( ) max 3f x t f x t+ − = 3 1t ≤ 1 1 3 3t− ≤ ≤ 1 1,3 3  −   ( ) 2sin cos cos 26 6 2f x x x x π π π     = + + + −           ( )f x 0, 2x π ∈   ( )f x 【答案】（1） ；（2） . 【解析】 【分析】 （1）利用三角恒等变换思想化简函数 的解析式为 ，利用 正弦型函数的周期公式可计算出函数 的最小正周期； （2）由 可计算出 的取值范围，利用正弦函数的基本性质可得出函数 在区间 0,π2 上的值域. 【详解】（1） ， 则函数 的最小周期为 ； （2）当 时， ，则 ， ， 因此，当 时，函数 的值域为 . 【点睛】本题考查正弦型函数最小正周期和值域的求解，解答的关键就是利用三角恒等变换 思想化简函数解析式，考查计算能力，属于中等题. 19.如图，已知四棱锥 ， 是等边三角形， ， ， π 3 , 32  −    ( )y f x= ( ) 3sin 2 6f x x π = +   ( )y f x= 0, 2x π ∈   2 6x π+ ( )y f x= ( ) 2sin cos cos 2 sin 2 sin 26 6 2 3f x x x x x x π π π π       = + + + − = + +               1 3 3 3sin 2 cos2 sin 2 sin 2 cos2 3sin 22 2 2 2 6x x x x x x π = + + = + = +   ( )y f x= 2 2T π π= = 0, 2x π ∈   72 ,6 6 6x π π π + ∈   1 sin 2 12 6x π − ≤ + ≤   ( )3 32 f x∴− ≤ ≤ 0, 2x π ∈   ( )y f x= 3 , 32  −    P ABCD− PCD∆ //AB CD AB AD⊥ ， ， 是 的中点． （1）求证：直线 平面 ； （2）求直线 与平面 所成角的正弦值． 【答案】（1）证明见解析；（2） . 【解析】 【分析】 （1）取 的中点 ，连接 、 ，通过证明四边形 为平行四边形得出 ，再利用线面平行的判定定理可得出结论； （2）以 为原点， 、 、过 D 且垂直底面的直线分别为 、 、 轴建立空间直角坐 标系，设 ，根据已知条件求出点 的坐标，可得出点 的坐标，然后利用空间向量法 可求出直线 与平面 所成角的正弦值． 【详解】（1）取 的中点 ，连接 、 ， 根据中位线定理， ，且 ， 又 ，所以 ， ，则四边形 为平行四边形， ， 平面 ， 平面 ， 平面 ； （2）以 为原点， 、 、过 D 且垂直底面的直线分别为 、 、 轴建立空间直角坐 标系， 1 2AB AD CD= = PA PD= E PC //BE PAD BE ABCD 66 12 PD G AG EG ABEG //BE AG D DA DC x y z 1AB = P E BE ABCD PD G AG EG //EG CD 1 2EG CD AB= = //AB CD //AB EG AB EG= ABEG //BE AG∴ BE ⊄ PAD AG ⊂ PAD //BE∴ PAD D DA DC x y z 设 ，则 、 、 、 ，设 ， 由 ， ， ， 上面联立解方程组得 ， ， ， 故点 ，所以 ，得到 ， 平面 的法向量为 ，由 . 故直线 与平面 所成角的正弦值为 ． 【点睛】本题考查直线与平面平行的证明，同时也考查了利用空间向量法计算直线与平面所 成角的正弦值，考查推理能力与计算能力，属于中等题. 20.已知 是圆 上一点， ， ，其中 ． （1）若直线 与圆 相切，求直线 的方程： （2）若存在两个点 使得 ，求实数 的取值范围． 1AB = ( )0,0,0D ( )1,0,0A ( )1,1,0B ( )0,2,0C ( ), ,P x y z 2 2 2 2DP x y z= + + = ( )2 2 21 2AP x y z= − + + = ( )22 22 2CP x y z= + − + = 1 2x = 1y = 11 2z = 1 11,1,2 2P       1 3 11, ,4 2 4E       3 1 11, ,4 2 4BE  = −     ABCD ( )0,0,1m = 11 664cos , 1261 2 m BEm BE m BE ⋅= = = ⋅ ×   BE ABCD 66 12 P ( )22: 1 4C x y+ − = ( ),0A t ( )4,3B t + t R∈ AB C AB P PA PB⊥ t 【答案】（1） 或 ；（2） . 【解析】 【分析】 （1）求出直线 的方程，利用圆心到直线 的距离等于圆的半径可求出实数 的值，进 而可得出直线 的方程； （2）求出以 为直径的圆的方程，确定该圆的圆心坐标和半径长，结合已知条件转化为两 圆相交即可求得实数 的取值范围. 【详解】（1）已知 是圆 上一点， ， . 圆心 为 ，半径 ，直线 的斜率为 . 直线 的方程为 ，即 . 直线 与圆 相切， ，解得 或 . 因此，直线 的方程为 或 ； （2）因为 、 ， 所以 的中点 ，且 . 则以 为直径的圆的圆心为 ，半径为 . 存在两个点 使得 ，所以圆 与圆 相交， 即 ，即 ， 3 4 6 0x y− − = 3 4 14 0x y− + = ( ) ( )2 5 2, 2 2,2 5 2− − − − − AB AB t AB AB t P ( )22: 1 4C x y+ − = ( ),0A t ( )4,3B t + C ( )0,1 2r = AB ( ) 3 0 3 4 4ABk t t −= =+ − ∴ AB ( )3 4y x t= − 3 4 3 0x y t− − =  AB C ( )22 3 0 4 1 3 3 42 53 4 t t× − × − +∴ = = + − 2t = 14 3t = − AB 3 4 6 0x y− − = 3 4 14 0x y− + = ( ),0A t ( )4,3B t + AB 32, 2D t +   2 23 4 5AB = + = AB 32, 2D t +   5 2R =  P PA PB⊥ C D R r CD R r− < < + ( ) 2 21 3 92 12 2 2t  < + + − <   解得 且 . 因此，实数 取值范围是 . 【点睛】本题考查直线与圆 位置关系，考查利用直线与圆相切求直线方程，以及与圆相关 的动点问题，将问题转化为两圆的位置关系是解答的关键，考查化归与转化思想的应用，属 于中等题. 21.已知数列 满足 ， ，记 ． （1）求 和 ； （2）证明： ． 【答案】（1） ， ；（2）证明见解析. 【解析】 【分析】 （ 1 ） 令 求 出 的 值 ， 令 ， 由 得 出 ，两式相减可得出 ，再对 的值进行验证即可得 出数列 的通项公式，进而利用等比数列求和公式可得出 ； （2）利用导数证明出不等式 ，可得出 ，利用不等式的性质 可得出 ，再由 进而可证明出结论成立. 【详解】（1）数列 满足 ， . 当 时， ； 的 的 2 5 2 2 5 2t− − < < − 2t ≠ − t ( ) ( )2 5 2, 2 2,2 5 2− − − − − { }na ( )1 2 2 33 2 1 3 2n n na a n a ++ + + − = − n ∗∈N 1 2n nS a a a= + + + na nS 1 1 11 ln 12 3 nS nn  + + + + < +   1 2n na = 11 2n nS = - 1n = 1a 2n ≥ ( )1 2 2 33 2 1 3 2n n na a n a ++ + + − = − ( )1 2 1 1 2 13 2 3 3 2n n na a n a − − ++ + + − = − na 1a { }na nS ( )ln 1 0x x x≤ − > 1 1ln 1 n n n + > + 1 1 11 ln 12 3 nn + + + + < + 1nS < { }na ( )1 2 2 33 2 1 3 2n n na a n a ++ + + − = − n ∗∈N 1n = 1 5 13 2 2a = − = 当 时，由 得 ， 两式相减得 ， ， 满足 ，所以，对任意 ， . ，所以，数列 是等比数列，且首项和公比均为 ， 因此， ； （2）先证明 ． 令 ，则 ，由 . 当 时， ；当 时， . 所以，函数 的单调递增区间为 ，单调递减区间为 ， 当 时，函数 取得最大值，即 ， 当 时， . 令 ，则 ，化为 ， 则 ， ， ， ， 上述不等式全部相加得 ，则 ， 的 2n ≥ ( )1 2 2 33 2 1 3 2n n na a n a ++ + + − = − ( )1 2 1 1 2 13 2 3 3 2n n na a n a − − ++ + + − = − ( ) ( ) 1 4 2 2 32 1 2 3 2 12 1 2 2 2 2n n n n n n nn n nn a − + − ++ + −− = − = = 1 2n na∴ = 1 1 2a = 1 2n na = n ∗∈N 1 2n na = 11 1 1 2 12 1 2 2 2 nnn n n n a a ++ += = = { }na 1 2 1 11 12 2 11 21 2 n n nS  −  = = − − ( )ln 1 0x x x≤ − > ( ) ln 1f x x x= − + ( ) 1 11 xf x x x −= − =′ ( ) 0 1f x x=′ ⇒ = 0 1x< < ( ) 0f x′ > 1x > ( ) 0f x′ < ( )y f x= ( )0,1 ( )1,+∞ 1x = ( )y f x= ( ) ( )max 1 0f x f= = 0 1x< < ( ) 0f x < ( )0,11 nx n = ∈+ 1ln 11 1 1 n n n n n < − = −+ + + ( ) 1ln 1 ln 1n n n + − > + 1ln 2 ln1 2 − > 1ln3 ln 2 3 − >  ( ) 1ln ln 1n n n − − > 1 1 1ln 2 3n n > + + + 1 1 11 ln 12 3 nn + + + + < + ，所以， . 【点睛】本题考查利用数列的递推公式求数列的通项公式，同时也考查了等比数列求和以及 数列不等式的证明，涉及导数的应用，考查推理能力与计算能力，属于难题. 22.已知 ，函数 （其中 是自然对数的底数， ）． （1）当 时，求曲线 在点 处的切线方程； （2）若当 时都有 成立，求整数 的最大值． 【答案】（1） ；（2） . 【解析】 【分析】 （1）将 代入函数 的解析式，求出 和 的值，利用点斜式可得出所 求切线的方程； （2）由 结合参变量分离法得出 对任意的 恒成立，构造函数 ，利用导数求出函数 在 上的最小值，即可得出整数 的最大值. 【详解】（1）当 时， ， ，根据题意可得 ， ， 故曲线 在点 处的切线方程 ； （2）由 时都有 成立，可得 ， 11 2n nS = − 1 1 1 1 1 11 1 ln 12 3 2 3nS nn n  + + + + < + + + + < +    k ∈R ( ) xf x e kx= − e e 2.718=  1k = ( )y f x= ( )( )0, 0f 0x > ( ) ( )2 3 2 1f x x x k> + + + k 1y = 2− 1k = ( )y f x= ( )0f ( )0f ′ ( ) ( )2 3 2 1f x x x k> + + + 2 3 2 2 xe x xk x − − −< + 0x > ( ) 2 3 2 12 2 x xe x x eg x xx x − − −= = − −+ + ( )y g x= ( )0, ∞+ k 1k = ( ) xf x e x= − ( ) 1xf x e′ = − ( )0 1f = ( )0 0f ′ = ( )y f x= ( )( )0, 0f 1y = 0x > ( ) ( )2 3 2 1f x x x k> + + + 2 3 2 2xe kx x x k− > + + + 得 ， 构造函数 ，则 ， ， 令 ， ， 则 ，令 ，得 . 当 时， ；当 时， . 所以，函数 在 上单调递减，在 上单调递增， 则 ， 又 ， ， ， ， 所以，存在 ，使得 ，得 . 当 时， ，即 ，此时，函数 单调递减； 当 时， ，即 ，此时，函数 单调递增. 所以， ， 构造 ，其中 ，则 ， ( )2 3 2 12 2 x xe x x ek xx x − + + < = − −+ + ( ) ( )1 02 xeg x x xx = − − >+ ( )mink g x< ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 1 21 2 2 x xx e x e xg x x x + + − +′ = − = + + ( ) ( ) ( )21 2xh x x e x= + − + 0x > ( ) ( ) ( ) ( )( )2 2 2 2 2x xh x x e x x e′ = + − + = + − ( ) 0h x′ = ln 2x = 0 ln 2x< < ( ) 0h x′ < ln 2x > ( ) 0h x′ > ( )y h x= ( )0,ln 2 ( )ln 2,+∞ ( ) ( ) ( ) ( ) ( )2 2 min ln 2 2 ln 2 1 2 ln 2 ln 2 2ln 2 2 0h x h= = + − + = − − − < ( )0 3 0h = − < ( )1 2 9 0h e= − < 3 23 5 49 02 2 4h e  = − <   ( ) 22 3 16 0h e= − > 3 ,22t  ∈   ( ) ( ) ( )21 2 0th t t e t= + − + = ( )22 1 t te t += + 0 x t< < ( ) 0h x < ( ) 0g x′ < ( )y g x= x t> ( ) 0h x > ( ) 0g x′ > ( )y g x= ( ) ( ) ( )2 min 2 2 111 1 12 2 1 1 t t e ttg x g t t t t tt t t t + ++= = − − = − − = − − = −+ + + + ( ) 1 1t tt ϕ = −+ 3 22 t< < ( ) ( )2 1 1 0 1 t t ϕ′ = − − < + 所以，函数 在区间 上单调递减，则 ， 又 对任意的 恒成立，因此，整数 的最大值为 . 【点睛】本题考查利用导数求函数的切线方程，同时也考查了利用导数求解函数不等式恒成 立问题，涉及隐零点法的应用，考查化归与转化思想的应用，属于难题. ( ) 1 1t tt ϕ = −+ 3 ,22      ( )5 11 3 10g t− < < − ( )k g x< 0x > k 2−