2020年高二数学下学期期末复习备考之精准复习模拟题文（C卷02）江苏版

2020年高二数学下学期期末复习备考之精准复习模拟题文（C卷02）江苏版

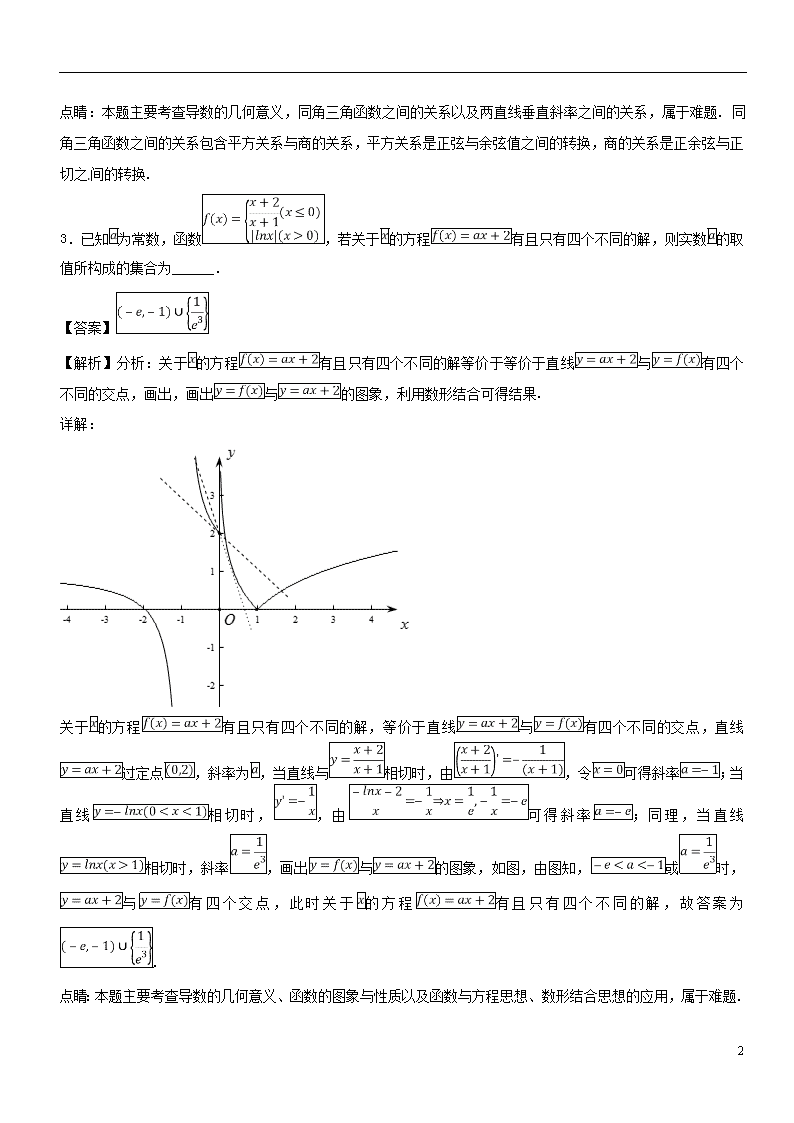
‎2017-2018学年高二数学下学期期末复习备考之精准复习模拟题 文（C卷02）江苏版 一、填空题 ‎1．已知直线，分别与直线和曲线交于点M,N两点，则线段MN长度的最小值是______．‎ ‎【答案】‎ 点睛：本题主要考查导数的几何意义以及转化与划归思想，属于难题. 求曲线切线方程的一般步骤是：（1）求出在处的导数，即在点 出的切线斜率（当曲线在处的切线与轴平行时，在 处导数不存在，切线方程为）；（2）由点斜式求得切线方程.‎ ‎2．已知两曲线，相交于点P，若两曲线在点P处的切线互相垂直，则实数的值是______．‎ ‎【答案】‎ ‎【解析】分析：联立两曲线方程，可得，设交点，分别求出的导数，可得切线的斜率，由两直线垂直的条件：斜率之积为，再由同角基本关系式，化弦为切，解方程即可得到值.‎ 详解：由，即，即有，设交点，的导数为的导数为，由两曲线在点处的切线相互垂直，可得 ‎，且，则，分子分母同除以，即有，可得，解得或（舍去），故答案为.‎ 22‎ 点睛：本题主要考查导数的几何意义，同角三角函数之间的关系以及两直线垂直斜率之间的关系，属于难题. 同角三角函数之间的关系包含平方关系与商的关系，平方关系是正弦与余弦值之间的转换，商的关系是正余弦与正切之间的转换.‎ ‎3．已知为常数，函数，若关于的方程有且只有四个不同的解，则实数的取值所构成的集合为______．‎ ‎【答案】‎ ‎【解析】分析：关于的方程有且只有四个不同的解等价于等价于直线与有四个不同的交点，画出，画出与的图象，利用数形结合可得结果.‎ 详解：‎ 关于的方程有且只有四个不同的解，等价于直线与有四个不同的交点，直线过定点，斜率为，当直线与相切时，由，令可得斜率；当直线相切时，，由可得斜率；同理，当直线相切时，斜率，画出与的图象，如图，由图知，或时，与有四个交点，此时关于的方程有且只有四个不同的解，故答案为.‎ 点睛：本题主要考查导数的几何意义、函数的图象与性质以及函数与方程思想、数形结合思想的应用，属于难题. ‎ 22‎ 数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，.函数图象是函数的一种表达形式，它形象地揭示了函数的性质，为研究函数的数量关系提供了“形”的直观性．归纳起来，图象的应用常见的命题探究角度有：1、确定方程根的个数；2、求参数的取值范围；3、求不等式的解集；4、研究函数性质．‎ ‎4．若函数有3个不同的零点，则实数的取值范围是 ______ ．‎ ‎【答案】‎ 则，绘制函数的图象如图所示，‎ 函数有3个不同的零点，‎ 则函数与函数有个不同的交点，‎ 观察函数图象可得：.‎ 点睛：函数零点的求解与判断方法：‎ 22‎ ‎(1)直接求零点：令f(x)＝0，如果能求出解，则有几个解就有几个零点．‎ ‎(2)零点存在性定理：利用定理不仅要函数在区间[a，b]上是连续不断的曲线，且f(a)·f(b)＜0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．‎ ‎(3)利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．‎ ‎5．已知函数是定义在上的偶函数，为奇函数，时， ，则在区间(4，5)内满足方程的实数的值为______．‎ ‎【答案】‎ ‎6．已知函数， ，若两函数与的图像有三个不同的公共点，则的范围为__________．‎ ‎【答案】‎ 22‎ 把原点代入切线方程得，得，‎ 要使得直线与交于三个不同的点，则，‎ 联立，解得，所以，则，‎ 所以的取值范围是.‎ 点睛：函数零点的应用主要表现在利用零点求参数范围，若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用.‎ ‎7．已知函数，设关于的方程（）有4个不同的实数解，则的取值范围是__________．‎ ‎【答案】或 22‎ 作出函数的图象，如图所示，‎ 由得或，‎ 由图象可知有两解，所以也有两解，‎ 所以或.‎ 点睛：本题主要考查了方程的根与函数的图象之间的关系的应用，其中解答中涉及到利用导数判定函数的单调性、利用导数求解函数的极值等知识点综合应用，其中把方程的根的个数转化为函数的图象的交点个数是解答的关键，着重考查了学生分析问题和解答问题的能力，以及数形结合思想的应用.‎ ‎8．设是定义在上的可导函数，且满足，则不等式 的解集为________．‎ ‎【答案】‎ ‎【解析】∵，‎ ‎∴函数在上单调递增。‎ 22‎ ‎∵，‎ ‎∴,‎ 即，‎ ‎∴,‎ ‎∴，解得。‎ 所以原不等式的解集为。‎ 答案： 。‎ ‎9．已知函数，，若存在，使得.则实数的取值范围是__________.‎ ‎【答案】‎ ‎【点睛】‎ 本题的解题关键是利用导数工具和函数的单调性取得函数，再利用图像的对称原原理将问题转化为，从而求得正解.‎ ‎10．设函数，若对任意的，都有，则实数的取值范围是___.‎ 22‎ ‎【答案】‎ 故实数的取值范围是。‎ 答案： ‎ ‎11．已知函数的图象在点处的切线恰好与直线平行，若在区间上单调递减，则实数的取值范围是_______.‎ ‎【答案】‎ ‎【解析】∵，‎ ‎∴。‎ 由题意得，解得，‎ ‎∵，‎ 22‎ ‎∴，‎ 由，得，‎ 所以函数的单调减区间为。‎ 点睛：由函数的单调性求参数取值范围的方法 ‎（1）可导函数在某一区间上单调，实际上就是在该区间上（或）（在该区间的任意子区间内都不恒等于0）恒成立，通过分离参数转化为求函数的最值问题，从而获得参数的取值范围；‎ ‎（2）若已知在区间I上的单调性，区间I中含有参数时，可先求出的单调区间，令I是其单调区间的子集，从而可求出参数的取值范围．‎ ‎12．曲线在点处的切线方程为________。‎ ‎【答案】‎ ‎【解析】根据题意得到：另x=1得到 再另x=0得到 故得到，求导得到 ‎ 将点代入方程可得结果。‎ 由上述条件得到方程为： 。‎ 故答案为： 。‎ 22‎ ‎13．已知函数，若恒成立，则实数m的取值范围是 ‎____________。‎ ‎【答案】‎ ‎【解析】对任意b＞a＞2， ＜1恒成立，‎ 等价于f（b）﹣b＜f（a）﹣a恒成立；‎ ‎∴m≥；‎ ‎∴m的取值范围是[-2，+∞）．‎ 故答案为： 。‎ 点睛：本题考查了导数的综合应用问题，解题时应根据函数的导数判定函数的增减性以及求函数的极值和最值，应用分类讨论法，构造函数等方法来解答问题．对于函数恒成立或者有解求参的问题，常用方法有：变量分离，参变分离，转化为函数最值问题；或者直接求函数最值，使得函数最值大于或者小于0；或者分离成两个函数，使得一个函数恒大于或小于另一个函数。‎ ‎14．半径为1cm的球的半径以2 cm / s 的速度向外扩张，当半径为9cm 时，球的表面积增加的速度为_________cm2 / s．‎ ‎【答案】144‎ ‎【解析】根据球表面积S=4πR2得：‎ ‎=8πR×，其中=2，‎ 当半径R=9cm时，‎ ‎=8π×9×2=144πcm2/s 22‎ 故答案为：144π．‎ 二、解答题 ‎15．已知函数，.‎ ‎（1）若函数在区间上存在零点，求实数的取值范围；‎ ‎（2）当时，若对任意的，总存在使成立，求实数的取值范围；‎ ‎（3）若的值域为区间，是否存在常数，使区间的长度为？若存在，求出的值，若不存在，请说明理由.（柱：区间的长度为）‎ ‎【答案】(1) ；(2)；(3)答案见解析.‎ ‎【解析】试题分析：求出函数的对称轴，得到函数的单调性，解关于的不等式组，解出即可；‎ 只需函数的值域是函数的值域的子集，通过讨论，，的情况，得到函数的单调性，从而确定的范围即可；‎ 通过讨论的范围，结合函数的单调性以及，的值，得到关于的方程，解出即可。‎ ‎（2）若对任意的，总存在，使成立，‎ 只需函数的值域是函数的值域的子集，‎ 时，的值域是，‎ 下面求，的值域，‎ 令，则，，‎ ‎①时，是常数，不合题意，舍去；‎ ‎②时，的值域是，‎ 要使 ，只需，计算得出；‎ ‎③时，的值域是，‎ 22‎ 要使 ，只需，计算得出；‎ 综上，的范围是.‎ ‎（3）根据题意得，计算得出，‎ ‎①时，在区间上，最大，最小，‎ ‎，‎ 计算得出：或（舍去）；‎ 点睛：本题是道函数综合题目，在判定零点的时候可以运用零点的存在定理求解，当遇到“对任意的，总存在”时候要转化为两个函数值域的包含关系，从而求解。‎ ‎16．已知函数 ‎⑴若，且，求的值；‎ ‎⑵当时，若在上是增函数，求a的取值范围是；‎ ‎⑶若a=1，求函数在区间上的最大值.‎ ‎【答案】（1）；（2）；（3）.‎ ‎【解析】试题分析：（1）⇒，再由f（x）=-1即可求得x的值； （2）由, 在[2，+∞）上是增函数，利用二次函数的单调性可求得a的取值范围； ‎ 22‎ ‎（3）作出,的图象，对m分0＜m≤1与1＜m, 三种情况讨论即可求得答案．‎ 试题解析：‎ 解：(1)由知 即 ∴‎ ‎(2) ‎ 在 上是增函数 ‎ ‎ ‎∴‎ ‎(3) ‎ 图象如图 22‎ 当时，‎ 当时，‎ 当时，‎ 综合. ‎ ‎17．已知函数，‎ ‎（1）若的解集为，求的值；‎ ‎（2）求函数在上的最小值；‎ ‎（3）对于，使成立，求实数的取值范围．‎ ‎【答案】(1) .‎ ‎(2) .‎ ‎(3) .‎ 22‎ ‎（2）的对称轴方程为，‎ ‎①当时，即 在上是单调增函数，故；‎ ‎②当时，即，在上是单调减函数，在上是单调增函数，‎ 故；‎ ‎③当时，即 在上是单调减函数，故；‎ 所以 22‎ 由（2）知 ‎① ‎ 解得,所以；‎ ‎②当时,‎ 解得，所以；‎ ‎③当时， ‎ 解得，所以 ‎ 综上所述，的取值范围是. ‎ 点睛：该题考查的知识点由一元二次不等式的解集与一元二次方程根的关系、二次函数在某个闭区间上的最小值问题、有关恒成立问题的求解，在解题的过程中，需要应用根与系数的关系求得参数值，需要对参数进行讨论，讨论的标准就是对称轴与区间的关系，还有就是恒成立问题转化为函数的最值来处理，根据是任意还是存在，来确定是最大值还是最小值.‎ ‎18．已知函数．‎ ‎（1）若曲线在处的切线过点．‎ ‎① 求实数的值；‎ ‎② 设函数，当时，试比较与的大小；‎ ‎（2）若函数有两个极值点，（），求证：．‎ ‎【答案】(1)①;②见解析;(2)见解析.‎ ‎【解析】分析：（1）①求出函数的导数，得到切点，表示出切线方程，代入切点的坐标即可求解；‎ ‎②由，设 ，利用导数得到函数的单调性和最值，即可得到结论．‎ ‎（2）设通过讨论的范围，得到函数的单调性，根据 得到，进而得到，设，得到单调减函数，即可作出证明．‎ 详解：（1）①因为，所以，‎ ‎ 由曲线在处的切点为，‎ 22‎ 所以在处的切线方程为．‎ 因为切线过点，所以． ‎ ‎②，‎ 由． ‎ 设（），所以，‎ 所以在为减函数．‎ 因为，所以当时，有，则；当时，有，则；‎ 当时，有，则． ‎ ‎（2）由题意，有两个不等实根，（）．‎ 设，则（），‎ 当时，，所以在上是增函数，不符合题意；‎ 当时，由，得，‎ 列表如下：‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ 由题意， ‎ ‎，解得，所以，‎ 因为，所以． ‎ 因为，所以，‎ 所以（）．‎ 22‎ 点睛：本题主要考查导数在函数中的应用，着重考查了转化与化归思想、逻辑推理能力与计算能力.导数是研究函数的单调性、极值(最值)最有效的工具，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，求解曲线在某点处的切线方程； (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数； (3)利用导数求函数的最值(极值)，解决函数的恒成立与有解问题，同时注意数形结合思想的应用.‎ ‎19．已知函数.‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）若函数有两个极值点，且，求证；‎ ‎（3）设，对于任意时，总存在，使成立，求实数的取值范围.‎ ‎【答案】（1）递增区间为和,递减区间为.（2）见解析（3）‎ ‎【解析】分析：（1）求出，在定义域内，分别令求得的范围，可得函数增区间，求得的范围，可得函数的减区间；（2）在上有两个不等的实根,由韦达定理及对数的运算法则可得，只需利用导数证明即可；（3）只需成立即可.化简得,，所以在递增，，利用在上恒成立可得结果.‎ 详解：(1)‎ 22‎ 时,, ‎ 令或,令,‎ 所以的递增区间为和,递减区间为. ‎ ‎(2)由于有两个极值点,‎ 则在上有两个不等的实根,‎ ‎ ‎ ‎ ‎ ‎ 设，‎ 所以 所以在上递减，所以即.‎ 令，则在上恒成立，‎ ‎，又 当时，,在递减,当时，,‎ 22‎ 所以，所以；‎ 当即时，‎ ‎①即时，在上递增，‎ 存在，使得，不合；‎ ‎②即时，，在递减,‎ 当时，,所以，‎ 所以综上, 实数的取值范围为.‎ 点睛：本题主要考查利用导数求函数的单调性以及不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数恒成立(即可)或恒成立（即可）；② 数形结合( 图象在 上方即可)；③ 讨论最值或恒成立；④ 讨论参数.‎ ‎20．定义可导函数的弹性函数为；在区间D上，若函数的弹性函数值大于1，则称在区间D上具有弹性，相应的区间D也称作的弹性区间．‎ ‎(1)若，求的弹性函数及弹性函数的零点；‎ ‎(2)对于函数=（其中e为自然对数的底数），求的弹性区间D.‎ ‎【答案】（1）弹性函数为．其零点为.‎ ‎（2）‎ ‎【解析】试题分析：‎ ‎（1）由函数的解析式有结合弹性函数的定义可得的弹性函数为．其零点为.‎ ‎⑵由题意可得弹函数的解析式为，此不等式等价于不等式组：‎ ‎(Ⅰ)或(Ⅱ).‎ 分类讨论可知因不等式组(Ⅰ)的解为.不等式组(Ⅱ)无实数解．即的弹性区间.‎ 22‎ ‎⑵，函数定义域为。‎ 因为 ，‎ 的弹性函数，‎ 此不等式等价于下面两个不等式组，‎ ‎(Ⅰ)或(Ⅱ).‎ 因①对应的函数就是，‎ 由，所以在定义域上单调增，‎ 又，所以①的解为；‎ 而②，‎ 在上恒正，‎ 则在上单调递增，所以，故②在上恒成立.‎ 22‎ 点睛：导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出 ，本专题在高考中的命题方向及命题角度 从高考来看，对导数的应用的考查主要从以下几个角度进行： (1)考查导数的几何意义，往往与解析几何、微积分相联系． (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数． (3)利用导数求函数的最值(极值)，解决生活中的优化问题． (4)考查数形结合思想的应用．‎ 22‎