【数学】2020届一轮复习人教B版(文)选修4-5第1讲绝对值不等式作业
1.已知函数f(x)=|x-2|-|x-5|.
(1)证明:-3≤f(x)≤3;
(2)求不等式f(x)≥x2-8x+15的解集.
解: (1)证明:f(x)=|x-2|-|x-5|
=
当2
2时,由f(x)≥1解得x>2.
所以f(x)≥1的解集为{x|x≥1}.
(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.而
|x+1|-|x-2|-x2+x≤|x|+1+|x|-2-x2+|x|=-(|x|-)2+≤,
且当x=时,|x+1|-|x-2|-x2+x=.
故m的取值范围为.
3.(2019·广东五校协作体第一次诊断考试)已知函数f(x)=|x-a|,其中a>1.
(1)当a=3时,求不等式f(x)≥4-|x-4|的解集;
(2)若函数h(x)=f(2x+a)-2f(x)的图象与x轴,y轴围成的三角形面积大于a+4,求a
的取值范围.
解:(1)当a=3时,f(x)+|x-4|=,
当x≤3时,由f(x)≥4-|x-4|得,-2x+7≥4,解得x≤;
当3<x<4时,f(x)≥4-|x-4|无解;
当x≥4时,由f(x)≥4-|x-4|得,2x-7≥4,解得x≥;
综上f(x)≥4-|x-4|的解集为{x|x≤或x≥}.
(2)因为h(x)=f(2x+a)-2f(x),所以h(x)=
所以S=×2a×>a+4,解得a>4.
4.(2018·高考全国卷Ⅱ)设函数f(x)=5-|x+a|-|x-2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
解:(1)当a=1时,f(x)=
可得f(x)≥0的解集为{x|-2≤x≤3}.
(2)f(x)≤1等价于|x+a|+|x-2|≥4.
而|x+a|+|x-2|≥|a+2|,且当x=2时等号成立.
故f(x)≤1等价于|a+2|≥4.
由|a+2|≥4可得a≤-6或a≥2.
所以a的取值范围是(-∞,-6]∪[2,+∞).
1.(2018·高考全国卷Ⅲ)设函数f(x)=|2x+1|+|x-1|.
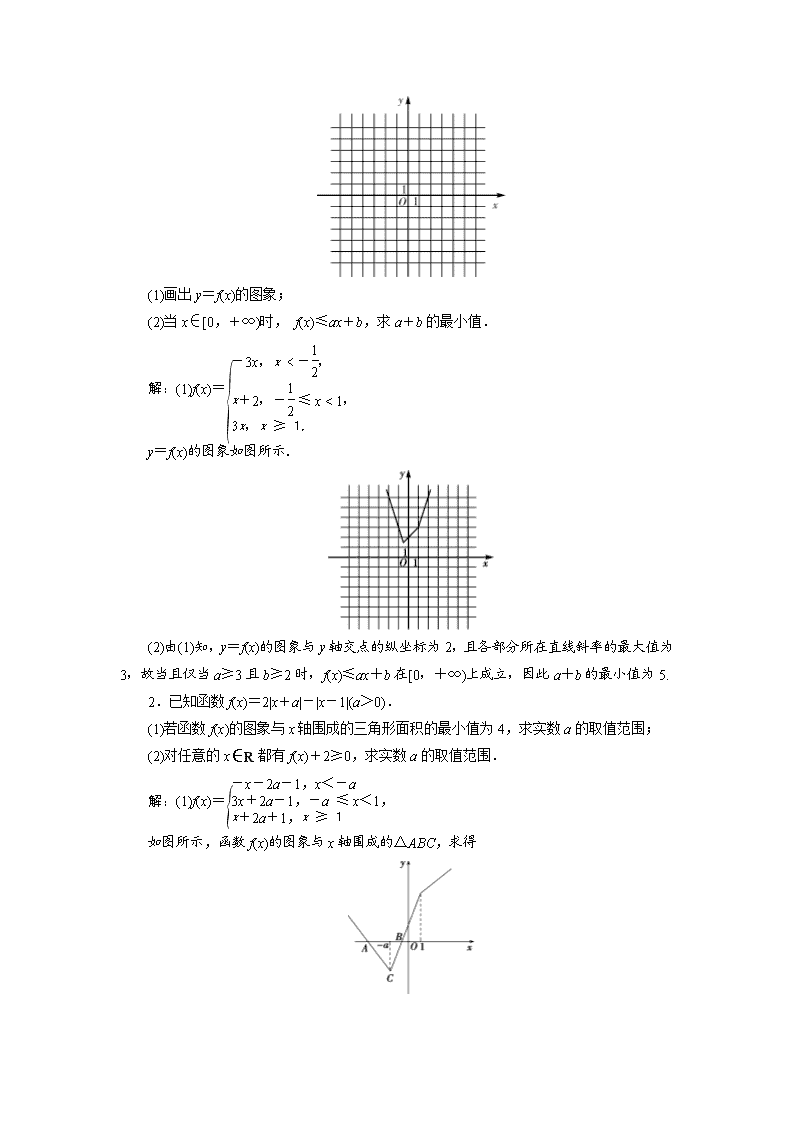
(1)画出y=f(x)的图象;
(2)当x∈[0,+∞)时, f(x)≤ax+b,求a+b的最小值.
解:(1)f(x)=
y=f(x)的图象如图所示.
(2)由(1)知,y=f(x)的图象与y轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当a≥3且b≥2时,f(x)≤ax+b在[0,+∞)上成立,因此a+b的最小值为5.
2.已知函数f(x)=2|x+a|-|x-1|(a>0).
(1)若函数f(x)的图象与x轴围成的三角形面积的最小值为4,求实数a的取值范围;
(2)对任意的x∈R都有f(x)+2≥0,求实数a的取值范围.
解:(1)f(x)=
如图所示,函数f(x)的图象与x轴围成的△ABC,求得
A(-2a-1,0),B(,0),C(-a,-a-1).
所以S△ABC=[-(-2a-1)]×|-a-1|=(a+1)2≥4(a>0),解得a≥-1.
(2)由(1)中图,可知f(x)min=f(-a)=-a-1,
对任意的x∈R都有f(x)+2≥0,
即(-a-1)+2≥0,解得0<a≤1.
3.(2019·合肥第一次教学质量检测)已知函数f(x)=|x-m|-|x+3m|(m>0).
(1)当m=1时,求不等式f(x)≥1的解集;
(2)对于任意实数x,t,不等式f(x)<|2+t|+|t-1|恒成立,求m的取值范围.
解:(1)f(x)=|x-m|-|x+3m|=
当m=1时,由,或x≤-3,得x≤-,所以不等式f(x)≥1的解集为{x|x≤-}.
(2)不等式f(x)<|2+t|+|t-1|对任意的实数t,x恒成立,等价于对任意的实数x,f(x)<(|2+t|+|t-1|)min恒成立,即[f(x)]max<(|2+t|+|t-1|)min,
因为f(x)=|x-m|-|x+3m|≤|(x-m)-(x+3m)|=4m,
|2+t|+|t-1|≥|(2+t)-(t-1)|=3,
所以4m<3,又m>0,所以0<m<.
4.(2019·湘中各校联考)已知函数f(x)=|x-2|+|2x+a|,a∈R.
(1)当a=1时,解不等式f(x)≥5;
(2)若存在x0满足f(x0)+|x0-2|<3,求实数a的取值范围.
解:(1)当a=1时,f(x)=|x-2|+|2x+1|.
由f(x)≥5得|x-2|+|2x+1|≥5.
当x≥2时,不等式等价于x-2+2x+1≥5,解得x≥2,所以x≥2;
当-<x<2时,不等式等价于2-x+2x+1≥5,即x≥2,所以解集为空集;
当x≤-时,不等式等价于2-x-2x-1≥5,解得x≤-,所以x≤-.
综上原不等式的解集为{x|x≤-或x≥2}.
(2)f(x)+|x-2|=2|x-2|+|2x+a|=|2x-4|+|2x+a|≥|2x+a-(2x-4)|=|a+4|,
因为原命题等价于(f(x)+|x-2|)min<3,即|a+4|<3,所以-7<a<-1.