2017年高考真题——理科数学（浙江卷） 原卷版

2017年高考真题——理科数学（浙江卷） 原卷版

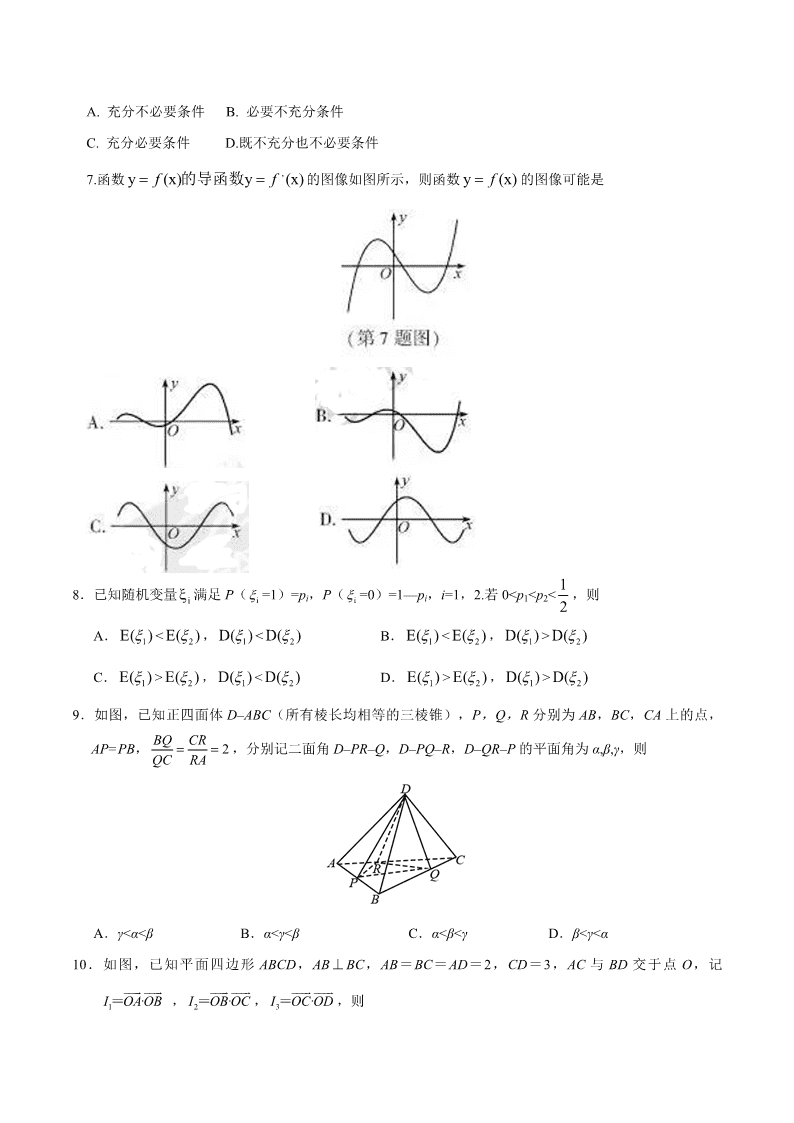
绝密★启用前 2017 年普通高等学校招生全国统一考试（浙江卷） 数 学 一、 选择题：本大题共 10 小题，每小题 4 分，共 40 分。每小题给出的四个选项中，只有一项是符合题目 要求的。 1.已知集合 ，那么 A.（-1,2） B.（0，1） C.（-1,0） D.（1,2） 2.椭圆 的离心率是 A. B. C. D. 3.某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位： ）是 A. B. C. D. 4.若 x,y 满足约束条件 的取值范围是 A.[0,6] B. [0,4] C.[6, D.[4, 5.若函数 在区间[0,1]上的最大值是 M,最小值是 m,则 M-m A. 与 a 有关，且与 b 有关 B. 与 a 有关，但与 b 无关 C. 与 a 无关，且与 b 无关 D. 与 a 无关，但与 b 有关 6.已知等差数列 的公差为 d,前 n 项和为 ,则“d>0”是    x -1 < x Q x   1 ， = 0 x 2P P Q = x y  2 2 19 4 13 3 5 3 2 3 5 9 3cm  +12  +32 3 +12 3 +32 x 0 x y 3 0 x 2y 0         + - ，则z 2 - x y +） +）   2f x =  x ax b  na nS 4 6 5" + 2 "S S S 的 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D.既不充分也不必要条件 7.函数 的图像如图所示，则函数 的图像可能是 8．已知随机变量 满足 P（ =1）=pi，P（ =0）=1—pi，i=1，2.若 0 C． > ， < D． > ， > 9．如图，已知正四面体 D–ABC（所有棱长均相等的三棱锥），P，Q，R 分别为 AB，BC，CA 上的点， AP=PB， ，分别记二面角 D–PR–Q，D–PQ–R，D–QR–P 的平面角为 α,β,γ，则 A．γ<α<β B．α<γ<β C．α<β<γ D．β<γ<α 10．如图，已知平面四边形 ABCD，AB⊥BC，AB＝BC＝AD＝2，CD＝3，AC 与 BD 交于点 O，记 ， ， ，则 y (x) y (x)f f  ，的导函数 y (x)f i i i 1 2 1E( ) 2E( ) 1D( ) 2D( ) 1E( ) 2E( ) 1D( ) 2D( ) 1E( ) 2E( ) 1D( ) 2D( ) 1E( ) 2E( ) 1D( ) 2D( ) 2BQ CR QC RA  1 ·I OAOB ＝ 2 ·I OB OC ＝ 3 ·I OC OD ＝ A．I１0 当 n=1 时，x1=1>0 假设 n=k 时，xk>0， 那么 n=k+1 时，若 xk+1 0,则 ，矛盾，故 >0。 因此 所以 因此 （Ⅱ）由 得 记函数 函数 f(x)在[0,+∞）上单调递增，所以 =0, 因此 （Ⅲ）因为 所以 得 故 nx  1 10 In(1 ) 0k k kx x x      1kx  0( )nx n N   1 1 1ln(1 )n n n nx x x x      10 ( )n nx x n N     1 1 1ln(1 )n n n nx x x x      2 1 1 1 1 1 14 2 2 ( 2)ln(1 )n n n n n n n nx x x x x x x x            2( ) 2 ( 2)ln(1 )( 0)f x x x x x x      ( ) (0)f x f 2 1 1 1 1 12 ( 2)ln(1 ) ( ) 0n n n n nx x x x f x          1 12 ( N )2 n n n n x xx x n      1 1 1 1ln(1 )n n n n nx x x x x        1 1 2n nx  1 122 n n n n x x x x   1 1 1 1 12( ) 02 2n nx x     1 2 1 1 1 1 1 1 1 12( ) 2 ( ) 22 2 2 n n n nx x x           2 1 2n nx  1 2 1 1 ( N )2 2nn nx n     