2018-2019学年安徽省滁州市定远县西片区高二上学期期中考试数学（理）试题 解析版

2018-2019学年安徽省滁州市定远县西片区高二上学期期中考试数学（理）试题 解析版

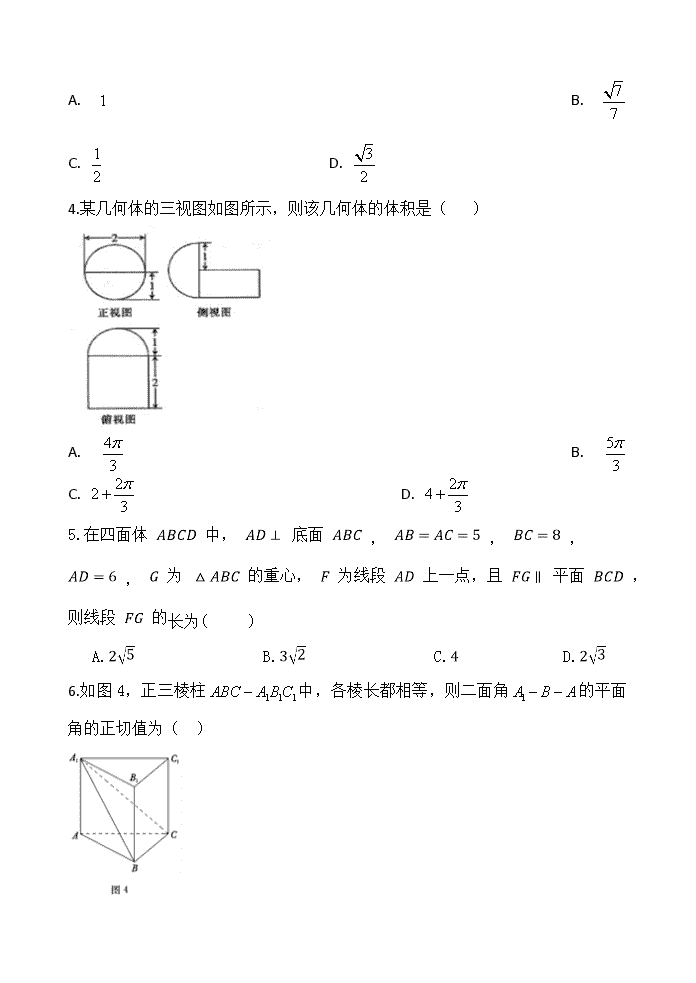
2018-2019 学年安徽省滁州市定远县西片区高二上学 期期中考试数学（理）试题 2018. 11 考生注意： 1、本卷考试范围：人教 A 版必修 2。满分 150 分，考试时间 120 分钟； 2、答题前请在答题卷上填写好自己的学校、姓名、班级、考号等信息； 3、请将答案正确填写在答题卷指定的位置，在非答题区位置作答无效。 第 I 卷 （选择题 60 分） 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中只有一项 符合题目要求。) 1.光线沿着直线 射到直线 上，经反射后沿着直线 射 出，则由（ ） A. ， B. ， C. ， D. ， 2.若圆 的圆心到直线 的距离为 ，则 的值为 （ ）． A. 或 B. 或 C. 或 D. 或 3. 在 三 菱 柱 中 ， 是 等 边 三 角 形 ， 平 面 ， ， ，则异面直线 和 所成角的正弦值为（ ） 3y x b= − + 0x y+ = 3y ax= − + 1 3a = 9b = − 1 3a = − 9b = 3a = 1 9b = − 3a = − 1 9b = 2 2 2 4 0x y x y+ − − = 0x y a− + = 2 2 a 2− 2 1 2 3 2 2 0 2− 0 1 1 1ABC A B C− ABC 1AA ⊥ ABC 2AB = 1 2AA = 1AB 1BC A. B. C. D. 4.某几何体的三视图如图所示，则该几何体的体积是（ ） A. B. C. D. 5.在四面体 中， 底面 ， ， ， ， 为 的重心， 为线段 上一点，且 平面 ， 则线段 的长为( ) A. B. C. D. 6.如图 4，正三棱柱 中，各棱长都相等，则二面角 的平面 角的正切值为（ ） 1 7 7 1 2 3 2 4 3 π 5 3 π 22 3 π+ 24 3 π+ 1 1 1ABC A B C− 1A B A− − A. B. C. 1 D. 7.如图，三棱柱 中，侧棱 底面 ，底面三角形 是正三 角形， 是 中点，则下列叙述正确的是（ ） A. 与 是异面直线 B. 平面 C. D. 平面 8.已知圆 与直线 及 都相切，圆心在直线 上，则圆 的方程为（ ） A. B. C. D. 9.在三棱锥 中， 与 都是边长为 6 的正三角形，平面 平面 ，则该三棱锥的外接球的体积为（ ） A. B. C. 6 2 3 2 3 3 C 0x y− = 4 0x y− − = 0x y+ = C ( ) ( )2 21 1 2x y+ + − = ( ) ( )2 21 1 2x y− + + = ( ) ( )2 21 1 2x y− + − = ( ) ( )2 21 1 2x y+ + + = A BCD− ABC∆ BCD∆ ABC ⊥ BCD 5 15π 60π D. 10.一个几何体的三视图如图所示，其中俯视图为正方形，则该几何体最大的侧 面的面积为（ ） A.1 B. C. D.2 11.若直线 与曲线 有两个交点，则实数 的取 值范围是（ ） A. B. C. D. 12.设 为两个不重合的平面， 为两两不重合的直线，给出下列四个命题： ①若 ， ，则 ；②若 ， ， ， ，则 ； ③ 若 ， ， 则 ； ④ 若 ， ， 且 ， ，则 . 其中正确命题的序号是（ ） A. ①③ B. ①②③ C. ①③④ D. ②④ 第 II 卷（非选择题 90 分） 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 60 15π 20 15π ,α β , ,l m n / /α β l α⊂ / /l β m α⊂ n α⊂ / /m β / /n β / /α β / /l α l β⊥ α β⊥ m α⊂ n α⊂ l m⊥ l n⊥ l α⊥ 13.如图，半球内有一内接正四棱锥 ，该四棱锥的体积为 ，则该半 球的表面积为 ． 14. 已 知 的 顶 点 都 在 球 的 球 面 上 ， ， 三 棱 锥 的体积为 ，则该球的表面积等于_________. 15.如图，已知 AB 为圆 O 的直径，C 为圆上一动点， 圆 O 所在平面，且 PA=AB=2，过点 A 作平面 ，交 PB,PC 分别于 E,F，当三棱锥 P-AEF 体积最 大时， = ． 16.在平面直角坐标系中， 分别是 轴和 轴上的动点，若以 为直径 的圆 与直线 相切，则圆 面积的最小值为 ． 三、解答题(本大题共 6 小题,共 70 分) 17.（10 分）直线过点 P 且与 x 轴、y 轴的正半轴分别交于 A，B 两点，O 为 坐标原点，是否存在这样的直线满足下列条件：①△AOB 的周长为 12；②△AOB ABC∆ O 6, 8, 10AB BC AC= = = O ABC− 40 3 4 ,23      的面积为 6.若存在，求出方程；若不存在，请说明理由． 18. （12 分）在平面直角坐标系中，圆 ： 与 轴的正半轴交于点 ，以 为圆心的圆 ： （ ）与圆 交于 ， 两点. （1）若直线 与圆 切于第一象限，且与坐标轴交于 ， ，当直线 长最小 时，求直线 的方程； （2）设 是圆 上异于 ， 的任意一点，直线 、 分别与 轴交于点 和 ，问 是否为定值？若是，请求出该定值；若不是，请说明理由. 19. （12 分）如图，在四棱锥 中，底面 是边长为 的正方形，侧 棱 底面 ，且侧棱 的长是 ，点 分别是 的中点. （Ⅰ）证明： 平面 ； （Ⅱ）求三棱锥 的体积. 20. （12 分）如图，在四棱锥 中，已知 平面 ，且四边形 为直角梯形， ． O 2 2 4x y+ = x A A A ( )2 2 22x y r− + = 0r > O B C l O D E DE l P O B C PB PC x M N OM ON⋅ O ABCD− ABCD 2 OB ⊥ ABCD OB 2 , ,E F G , ,AB OD BC OD ⊥ EFG O EFG− P ABCD− PA ⊥ ABCD ABCD , 2, 12ABC BAD PA AD AB BC π∠ = ∠ = = = = = （1）求平面 与平面 所成二面角的余弦值； （2）点 是线段 上的动点，当直线 与 所成的角最小时，求线段 的 长． 21. （ 12 分 ） 如 图 ， 在 四 棱 锥 中 ， 四 边 形 为 直 角 梯 形 ， 平面 ， 为 的中点， ． （1）求证： 平面 ； （2）设 ，求点 到平面 的距离． 22. （12 分）如图，在正方体 中，E、F 分别是 、CD 的中点， （1）证明： ；（2）求异面直线 与 所成的角；（3）证明：平 面 平面 。 PAB PCD Q BP CQ DP BQ A CDFE− CDFE / / , ,CE DF EF FD AF⊥ ⊥ CEFD P AD 1 2EC FD= / /CP AEF 2, 3, 4EF AF FD= = = F ACD 1 1 1 1ABCD A B C D− 1BB 1AD D F⊥ AE 1D F AED ⊥ 1 1A FD 2018-2019 学年度上学期期中考试 高二理科数学参考答案 1.A 【解析】在直线 上任意取一点， ，则点 关于直线 的 对 称 点 在 直 线 上 ， 故 有 ， 即 ，结合所给的选项，只有 ， 合题意，故选 A. 2.C 【解析】圆 ， 化成标准方程为 ， 圆心 到直线的距离 ， 解得 或 ，故选 ． 3.A 【解析】如图，作 交 的延长线于 ，连接 ，则 就是异面 直 线 和 所 成 的 角 （ 或 其 补 角 ），由 已 知 ， ，由 ，知 异面直线 和 所成的角为直角，正弦值为 ，故选 A. 3y x b= − + ( )1, 3A b − A 0x y+ = ( )3, 1B b− + − 3y ax= − + ( )1 3 3a b− = − − + + 3 4 0ab a− + = 1 3a = 9b = − 2 2 2 4 0x y x y+ − − = ( ) ( )2 21 2 5x y− + − = ( )1,2 ( )22 1 2 2 21 1 ad − += = + − 0a = 2 C 1/ /BD AB 1 1A B D 1DC 1DBC∠ 1AB 1BC ( )222 2 6BD = + = 1 16, 2 3BC C D= = 2 2 2 1 1BD BC C D+ = 1 90 ,DBC∠ = ∴ 1AB 1BC 1 4.B 【解析】由三视图得该几何体是由半个球和半个圆柱组合而成，根据图中所给数 据得该几何体的体积为 ,故选 B. 5.A 【解析】 如图，延长 AG 交 BC 于点 H，过点 G 作 GE//BC 交 AC 于点 E，过点 E 作 EF//DC， 交 AD 于点 F，则平面 EFG//平面 BCD，又 FG 平面 BCD，所以 FG//平面 BCD，又 ，所以 , ，所以 . 6.D 【解析】设棱长为 的中点为 ，连接 ， 由正三棱柱 中，个棱长都相等， 可得 ， 所以二面角 的平面角为 ， 在 中， ，所以 ， 即二面角 的平面角的正切值为 ，故选 D. 7.C 【解析】 中， 与 在侧面 ，又不平行，故相交， 错误； 中， 与面 斜交，夹角为 ， 错误； 中， ， 是异面直线，且 ， ，所以 ，故 正确； 中， 与平面 有公共点 ，所以 与平面 相交， 错误．故选 ． 1 4 522 3 3 π ππ + =   ,a BC E 1 ,A E AE 1 1 1ABC A B C− 1 ,A E BC AE BC⊥ ⊥ 1A BC A− − 1A EA∠ Rt ABC∆ 3 2AE a= 1 1 2 3tan 33 2 AA aA EA AE a ∠ = = = 1A BC A− − 2 3 3 8.B 【解析】直线 和 的斜率均为 1，所以两直线平行． 因为圆 与直线 和 都相切，所以两平行线直线 和 间的距离即为所求圆 的直径，即 ，所以 半径 ． 因为圆心在直线 上，则可设圆心 为 ， 圆 与直线 相切，所以圆心 到直线 的距离等于半径，即 ， 解得 ，依题意可知 ，所以 ，则圆心为 ， 所以圆 方程为 ．故 B 正确． 9.D 【解析】取 中点分别为 ，连接 ，根据题意知： 易知三棱锥的外接球球心 在线段 上， 连接 ，有 ， 0x y− = 4 0x y− − = C 0x y− = 4 0x y− − = 0x y− = 4 0x y− − = C ( ) ( )22 0 4 2 2 2 1 1 d r − − = = = + − 2r = 0x y+ = C ( ),a a− C 0x y− = C 0x y− = ( ) 2 2 a a d a r − − = = = 1a = 0a > 1a = ( )1, 1− C ( ) ( )2 21 1 2x y− + + = AD BC， E F， EF AF DF， ， 3 3AF DF AF CF⊥ = =， 1 3 6 2 2EF AD∴ = = O EF OA OC， 2 2 2R AE OE= + 2 2 2R DF OF= + 2 2 23 6 2R OE  ∴ = +    2 2 2 3 63 2R OE  = + −    15R∴ = 三棱锥的外接球的体积为 。故答案选 10.C 【解析】由三视图可知几何体是一条侧棱与底面垂直，底面是正方形，四棱锥的 高为 2，底面正方形的对角线的长为 2， 四棱锥的 4 个侧面面积分别为： = ； = ； = ； = ． 最大侧面面积为： ．故选：C． 11.C 【解析】曲线方程可化为 ，其图像为半圆（如图所 示），其中 ．又直线 过定点 ，若直线与半圆有 两个不同交点，则 ，当直线与 相切时，有 ， 解得 ，故实数 ． 故答案为：C． ∴ 34 20 153 Rπ π= D 12.A 【解析】①若 ， ，则平面 内任意直线都与平面 平行，∴ ， 故①正确； ②若 ， ， ，则 也可以平行于 与 的交线，此时两平面不 平行，故②错误； ③ ，根据面面垂直的判定定理，可得 ，故③正确； ④若 ， ，若 可以与面斜 交，不一定垂直， 故④不正确；故选 A 13. 【解析】设所给半球的半径为 ，则四棱锥的高 ，则 ，所以 ，所以半球的表面积为 .所以答案是:6 π . 14. 【解析】依题意知△ABC 为直角三角形，其所在圆面的半径为 ，设三棱 / /α β l α⊂ α β / /l β m α⊂ n α⊂ / /m β m β α l lα β⊥  ， α β⊥ m α⊂ n α⊂ m n l m l n l⊥ ⊥ ， ， ， α 400π 1 52 AC = 锥 O-ABC 的高为 h，则由 得 ，设球 O 的半径为 R，则 由 得 ，故该球的表面积为 . 15. 【解析】 平面 ，则 ，又 平面 ， 平面 ，设 ，在 中， ，在 中， ， ， 时，三棱锥 P-AEF 体积最大为 ，此时， ， .故答案为: . 16. 【解析】由题意，圆心 到原点的距离与到直线的距离相等，所以面积最小时， 圆心在原点到直线的垂线中点上，则 ，则 ， 。 17. ＋ ＝1. 【解析】设直线的方程 ，若满足（1）可得 ，联立可解 ，即可得方程； （2）若满足，可得 ，同样可得方程，它们公共的方程即为所求. 试题解析： 设直线方程为 ＋ ＝1(a>0，b>0)， 若满足条件(1)，则 a＋b＋ ＝12，① 1 1 6 8 40 33 2 h× × × = 5 3h = 2 2 25h R+ = 10R = 400π 4 x 3 y 1( 0, 0)x y a ba b + = > > 2 2 4 212, 13a b a b a b + − − = + = ,a b 4 212, 13ab a b = + = 又∵直线过点 P( ，2)，∵ ＋ ＝1.② 由①②可得 5a2－32a＋48＝0， 解得 ，或 . ∴所求直线的方程为 ＋ ＝1 或 ＋ ＝1， 即 3x＋4y－12＝0 或 15x＋8y－36＝0. 若满足条件(2)，则 ab＝12，③ 由题意得， ＋ ＝1，④ 由③④整理得 a2－6a＋8＝0， 解得 ，或 . ∴所求直线的方程为 ＋ ＝1 或 ＋ ＝1， 即 3x＋4y－12＝0 或 3x＋y－6＝0. 综上所述：存在同时满足(1)(2)两个条件的直线方程，为 3x＋4y－12＝0. 18.（1） （2）是定值，定值为 4 【解析】（1）设直线 的方程为 ，即 ，由直线 与 圆 相 切 ， 得 ， 即 ， ， 当且仅当 时取等号，此时直线 的方程为 ． （2）设 ， ，则 ， ， 直线 的方程为： 2 2 0x y+ − = l 1( 0, 0)x y a ba b + = > > 0bx ay ab+ − = l O 2 2 2ab a b = + 2 2 1 1 1 4a b + = ( )2 2 2 2 2 2 2 1 14 16DE a b a ba b  = + = + + ≥   2 2a b= = l 2 2 0x y+ − = ( )0 0,B x y ( )( )1 1 1 0,P x y y y≠ ± ( )0 0,C x y− 2 2 0 0 4x y+ = 2 2 1 1 4x y+ = PB ( )0 1 1 1 0 1 y yy y x xx x −− = −− 直线 的方程为： 分别令 ，得 所以 为定值． 19.（Ⅰ）证明: 四边形 是边长为 的正方形， 是 的中点, 又 侧棱 底面 , 面 又 是等腰三角形， 是 的中点, . 同理 是等腰三角形， 是 的中点, 面 平面 （Ⅱ）侧棱 底面 , 面 由（Ⅱ）知： 平面 , 是三棱锥 到平面 的距离 分别是 的中点, ， , 四边形 是边长为 的正方形， 是 的中点 三角形 是等边三角形 PC ( )0 1 1 1 0 1 y yy y x xx x − −− = −− 0y = 1 0 0 1 1 0 0 1 0 1 0 1 , ,M N x y x y x y x yx xy y y y − += =− + OM ON⋅ = ( ) ( )2 2 2 22 2 2 2 1 0 0 11 0 0 1 2 2 2 2 0 1 0 1 4 4 4M N y y y yx y x yx x y y y y − − −−= = =− −  ABCD 2 E AB ∴ 5DE =  OB ⊥ ABCD AB ⊂ ABCD ∴ OB ⊥ AB  2, 1OB EB= = ∴ 5OE = ∴ 5,DE OE= = ∴ ODE∆ F OD ∴ EF OD⊥ 5,DG DG= = ∴ ODG∆ F OD FG OD∴ ⊥ EF FG F∩ = ,EF FG ⊂ EFG OD ⊥ EFG OB ⊥ ABCD BD ⊂ ABCD ∴ OB ⊥ BD  2, 2 2OB DB= = ∴ 2 3OD = OD ⊥ EFG O EFG F OD 3OF = 5,DE OE= = EF OD⊥ ∴ 2EF = 5,DG DG= = FH OD⊥ ∴ 2FG =  ABCD 2 ,E G ,AB BC ∴ 2EG = ∴ EFG ∴ 3 2EFGS =  20.（1） （2） 【解析】以 为正交基底建立如图所示的空间直角坐标系 ，则各 点的坐标为 ． （ 1 ） 因 为 平 面 ， 所 以 是 平 面 的 一 个 法 向 量 ， ． 因为 ． 设平面 的法向量为 ，则 ， 即 ，令 ，解得 ． 所以 是平面 的一个法向量，从而 ， 所以平面 与平面 所成二面角的余弦值为 ． （2） 因为 ，设 ， 又 ，则 ， 0 1 1 3 2G EOF EFGV V Sh− −= = = 3 3 2 2 5 5 5BQ BP= = Axyz ( ) ( ) ( ) ( )1,0,0 , 1,1,0 , 0,2,0 , 0,0,2B C D P AD ⊥ PAB PAB PCD ( ), ,m x y z= 2 0{ 2 2 0 x y z y z + − = − = 1y = 1, 1z x= = ( )1,1,1m = PCD PAB PCD 3 3 又 ， 从而 ， 设 ， 则 ， 当且仅当 ，即 时， 的最大值为 ． 因为 在 上是减函数，此时直线 与 所成角取得最小值． 又因为 ，所以 ． 21. （1）证明： （方法一）设线段 的中点为 ，连接 ． ∵ 为 的中点，∴ ∵ ，且 ，∴四边形 为平行四边形，∴ ． 又 ，∴平面 平面 ． ∵ 平面 ，∴ 平面 ． （方法二）设线段 的中点为 ，连接 ． [ ]1 2 , 1,3t tλ+ = ∈ 9 5t = 2 5 λ = 3 10 10 cosy x= 0, 2 π     CQ DP 2 21 2 5BP = + = 2 2 5 5 5BQ BP= = FD Q PQ CQ、 P AD / /PQ AF 1 2EC FD= / /EC FD CEFQ / /CQ EF ,CQ PQ Q AF EF F= =  / /PCQ AEF CP ⊂ PCQ / /CP AEF AF G PG EG、 ∵ 为 的中点， ∴ ，且 ． 又∵ ，且 ，∴ ，∴四边形 为平行四边形，∴ ． ∵ 平面 平面 ， ∴ 平面 （2）（方法一）∵四边形 为直角梯形， ． ∴四边形 为正方形， 为等腰直角三角形． ∴ ，即 ． 又∵ 平面 ，∴ ． 又 ，∴ 平面 ，面 平面 ， ∴平面 平面 过 作 于点 ，则 平面 ，即 为点 到平面 的距 离． ∵ ，∴ ，∴ ，点 到 平面 的距离为 （方法二）设点 到平面 的距离为 ． P AD / /PG FD 1 2PG FD= 1 2EC FD= / /EC FD / /PG EC GECP / /PC EG EG ⊂ ,AEF PC ⊄ AEF / /CP AEF CDFE 12, 4, 22EF FD EC FD= = = = CEFQ CDQ∆ 090FCD∠ = CD FC⊥ AF ⊥ CEFD AF CD⊥ FC AF F= CD ⊥ AFC CD ⊂ ACD ACD ⊥ AFC F FH AC⊥ H FH ⊥ ACD FH F ACD 3, 2 2AF FC= = 17AC = 3 2 2 6 34 1717 AF FCFH AC ×= = = F ACD 6 34 17 F ACD d ∵ ，∴ ，∴ ． 由方法一得， 平面 ，∴ ， ∴ ． 22. 【解析】（1）因为 平面 ，所以 ; （2）取 AB 中点 G，连接 ， 因为 F 是 CD 的中点， 所以 GF、AD 平行且相等， 可证 是平行四边形，所以 ， 设 与 相交于点 H，则 是 与 所成的角， 因为 E 是 的中点， 所以 ， 即 与 所成的角是 ； （3）由上可知 ， ， 所以 平面 AED， 从而得平面 平面 . F ACD A PCDV V− −= 1 1 3 3ACD FCDS d S AF∆ ∆=  PCD ACD S AFd S ∆ ∆ =  CD ⊥ AFC ,CD AC CD FC⊥ ⊥ 1 2 2 3 6 342 1 17 17 2 FC CD AF FC AFd ACAC CD ×= = = =    AD ⊥ 1 1CDD C 1AD D F⊥ 1 ,AG FG 1 1GFD A 1 1/ /AG D F 1AG AE 1AHA∠ AE 1D F 1BB 1 90AHA∠ =  AE 1D F 90 1AD D F⊥ 1AE D F⊥ 1D F ⊥ 1 1A FD ⊥ AED