高三数学(理数)总复习练习专题十一 立体几何
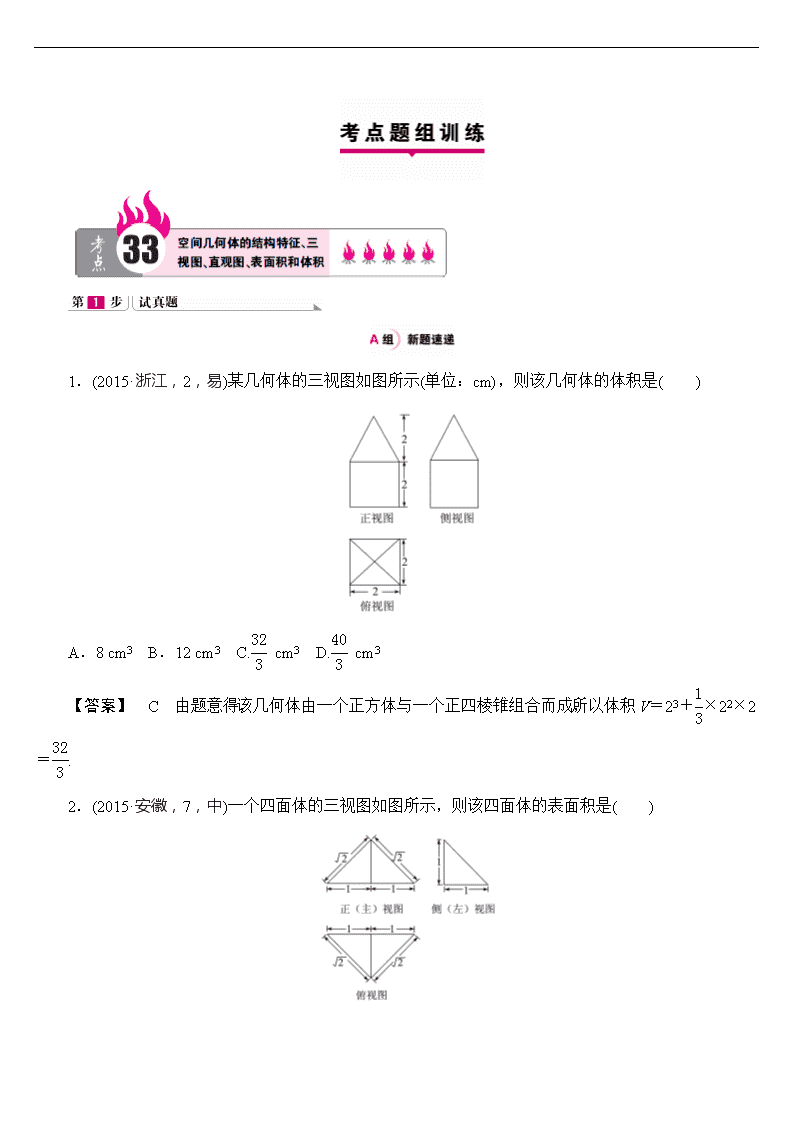
1.(2015·浙江,2,易)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
A.8 cm3 B.12 cm3 C. cm3 D. cm3
【答案】 C 由题意得,该几何体由一个正方体与一个正四棱锥组合而成,所以体积V=23+×22×2=.
2.(2015·安徽,7,中)一个四面体的三视图如图所示,则该四面体的表面积是( )
A.1+ B.2+ C.1+2 D.2
【答案】 B 将三视图还原为几何体,如图所示OABC,且OB==,
∴△OAC与△ABC为直角三角形,△OAB与△OBC为等边三角形.
∴S表=2S△OAC+2S△OAB
=2×××+2××()2
=2+.
3.(2015·山东,7,中)在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.2π
【答案】 C 如图,
以AD所在的直线为轴旋转一周,形成的几何体为一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥,所以其体积为V=π·12·2-·π·12·1=.故选C.
4.(2015·课标Ⅱ,6,中)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
A. B. C. D.
【答案】 D 如图所示为正方体被一个平面截去后剩余部分的几何体.
设正方体棱长为a,
∴==.
5.(2015·课标Ⅱ,9,中)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥OABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
【答案】 C 设球的半径为r,则VOABC=××r2h≤r3=36,故r=6.故S球=4πr2=144π.
6.(2015·课标Ⅰ,6,中)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A.14斛 B.22斛 C.36斛 D.66斛
【答案】 B 设圆锥底面半径为r,∵×2πr=8,
∴r=,∴V=××π××5=.设米堆共有x斛,则1.62x=,解得x≈22(斛).
7.(2015·课标Ⅰ,11,中)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )
A.1 B.2 C.4 D.8
【答案】 B 由题意知,该几何体是由半个圆柱与半个球组合得到的.
则表面积S=2πr2+2×πr2+4r2+2πr2=5πr2+4r2=20π+16,∴r=2.
8.(2015·江苏,9,中)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.
【解析】 设新的底面半径为r,根据题意得
π×52×4+π×22×8=πr2×4+8πr2,即28r2=196,∴r=.
【答案】
1.(2014·福建,2,易)某空间几何体的正视图是三角形,则该几何体不可能是( )
A.圆柱 B.圆锥 C.四面体 D.三棱柱
【答案】 A 因为圆锥、四面体、三棱柱的正视图均可以是三角形,而圆柱无论从哪个方向看均不可能是三角形,故选A.
2.(2013·广东,5,易)某四棱台的三视图如图所示,则该四棱台的体积是( )
A.4 B. C. D.6
【答案】 B 由四棱台的三视图可知,该四棱台的上底面是边长为1的正方形,下底面是边长为2的正方形,高为2,所以V=×(1+4+2)×2=.故选B.
思路点拨:解题的关键是由三视图判断几何体的结构特征并确定相应的数量关系.
3.(2014·湖南,7,中)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
A.1
B.2
C.3
D.4
【答案】 B 根据三视图得如图所示的三棱柱,即底面ABC是直角三角形的直棱柱.
要想得到最大的球,只需球与三个侧面都相切.因为直角三角形中,62+82=102,所以直角三角形ABC
的内切圆半径为r==2,故得到的最大球的半径为2.
4.(2014·安徽,7,中)一个多面体的三视图如图所示,则该多面体的表面积为( )
A.21+ B.18+
C.21 D.18
【答案】 A 由三视图知,该多面体是由正方体割去两个角后剩下的部分,如图所示,
则S=S正方体-2S三棱锥侧+2S三棱锥底=24-2×3××1×1+2××()2=21+.
5.(2013·课标Ⅰ,6,中)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )
A. cm3 B. cm3
C. cm3 D. cm3
【答案】 A 设球半径为R,如图所示,B为弦的中点,OA=OC=R,由垂径定理,知△OBA为直角三角形.
BC=2,BA=4,OB=R-2,OA=R,
由R2=(R-2)2+42,得R=5,
所以球的体积为π×53=π(cm3),故选A.
6.(2013·辽宁,10,中)已知三棱柱ABCA1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )
A. B.2
C. D.3
【答案】 C 方法一(补形法):过点C作AB的平行线,过点B作AC的平行线,交点为D,同理过点C1作A1B1的平行线,过点B1作A1C1的平行线,交点为D1,连接DD1,则ABCDA1B1C1D1恰好成为球的一个内接长方体,故球的半径r==.
方法二:如图,由球心作平面ABC的垂线,则垂足为BC的中点M.
又AM=BC=,OM=AA1=6,所以球O的半径R=OA==.
7.(2014·湖北,8,中)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈L2h相当于将圆锥体积公式中的π近似取为( )
A. B. C. D.
【答案】 B ∵V=πr2h=h=L2h,∴由V≈L2h得:L2h≈L2h,
即π≈.
8.(2014·天津,10,易)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.
【解析】 由三视图可知,该几何体是一个组合体,其上部是一个圆锥,底面圆半径为2,高为2,下部是一个圆柱,底面圆半径为1,高为4,故该几何体的体积V=·π·22·2+π·12·4=+
4π=.
【答案】
考向1 空间几何体的三视图与直观图
1.空间几何体的三视图
(1)几何体的三视图包括正(主)视图、侧(左)视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.
(2)三视图的画法
①基本要求:长对正,高平齐,宽相等.
②画法规则:正(主)侧(左)一样高,正(主)俯一样长,侧(左)俯一样宽;看不到的线画虚线.
2.用斜二测画法画几何体直观图的注意点
(1)用斜二测画法画几何体直观图时,要注意原图与直观图中的“三变”、“三不变”:
①“三变”
②“三不变”
(2)对于直观图,除了了解斜二测画法的规则外,还要了解原图形面积S与其直观图面积S′之间的关系:S′=S,并能进行相关的计算.
(1)(2014·湖北,5)在如图所示的空间直角坐标系Oxyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①②③④的四个图,则该四面体的正视图和俯视图分别为( )
A.①和② B.③和①
C.④和③ D.④和②
(2)(2013·四川,3)一个几何体的三视图如图所示,则该几何体的直观图可以是( )
【思路导引】 解题(1)的关键是先根据点的坐标画出几何体的直观图,再由直观图推测正视图和俯视图;解题(2)的方法是根据正视图和侧视图判断上面是台体、下面是柱体,再由俯视图可得答案.
【解析】 (1)如图,A(0,0,2),B(2,2,0),C(1,2,1),D(2,2,2),B,C,D点在面yOz上的射影分别为B1,C1,D1,它们在一条线上,且C1为B1D1的中点.从前往后看时,看不到棱AC,所以正视图中AC1应为虚线;故正视图应为图④.点A,D,C在面xOy内的射影分别为O,B,C2,俯视图为△OC2B,故俯视图应为图②.综上选D.
(2)由三视图可知该几何体为一个上部为圆台、下部为圆柱的组合体,圆台的下底面和圆柱的底面恰好重合.
【答案】 (1)D (2)D
1.由三视图还原直观图的方法
(1)还原后的几何体一般为较熟悉的柱、锥、台、球的组合体.
(2)注意图中实、虚线,实际是原几何体中的可视线与被遮挡线.
(3)想象原形,并画出草图后进行三视图还原,把握三视图和几何体之间的关系,与所给三视图比较,通过调整准确画出原几何体.
2.已知三视图中的某两个,求余下一个的三视图的方法
先根据已知的三视图中的某两个,还原、推测直观图的可能形式,找余下一个三视图的可能形式.作为选择题,也可将选项依次代入,再看看给出的三视图是否符合.
(1)(2014·江西,5)一个几何体的直观图如图,下列给出的四个俯视图中正确的是( )
(2)(2014·北京,7)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D,若S1,S2,S3分别是三棱锥DABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )
A.S1=S2=S3 B.S2=S1且S2≠S3
C.S3=S1且S3≠S2 D.S3=S2且S3≠S1
(1)【答案】 B 俯视图为在水平投射面上的正投影,结合几何体可知选B.
(2)【答案】 D 如图,在空间直角坐标系中,
S1=AB·BC=2,
S2=AB·DE=,
S3=BC·DE=,
∴S1>S2=S3,故选D.
考向2 空间几何体的表面积
1.多面体的侧面积和表面积
因为多面体的各个面都是平面,所以多面体的侧面积就是侧面展开图的面积,表面积是侧面积与底面积的和.
2.旋转体的侧面积和表面积
(1)若圆柱的底面半径为r,母线长为l,则
S侧=2πrl,S表=2πr(r+l).
(2)若圆锥的底面半径为r,母线长为l,则
S侧=πrl,S表=πr(r+l).
(3)若圆台的上、下底面半径分别为r′,r,则
S侧=π(r+r′)l,S表=π(r2+r′2+r′l+rl).
(4)若球的半径为R,则它的表面积S=4πR2.
(1)(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
(2)(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π C.9π D.
【思路导引】 解题(1)的关键是将三视图准确地还原成直观图,并弄清直观图中相对的位置关系;解题(2)的关键是根据题意,借助辅助面,画出相应的图形,求出半径.
【解析】 (1)根据几何体的三视图可得该几何体的直观图为如图所示的几何体ABCDEF,
故其表面积为S=S△DEF+S△ABC+S梯形ABED+S梯形CBEF+S矩形ACFD=×3×5+×3×4+×(5+2)×4+×(5+2)×5+3×5=60.
(2)如图所示,R2=(4-R)2+2,
∴R2=16-8R+R2+2,∴R=,
∴S表=4πR2=4π×=,选A.
【答案】 (1)B (2)A
求解空间几何体表面积的注意点
(1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.
(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.
(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.
(4)解决关于外接球的问题的关键是抓住外接的特点,即球心到多面体的顶点的距离都等于球的半径,同时要作一圆面起衬托作用.
(1)(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90 cm2 B.129 cm2
C.132 cm2 D.138 cm2
(2)(2013·福建,12)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是________.
(1)【答案】 D 由题干中的三视图可得原几何体如图所示.
故该几何体的表面积S=2×4×6+2×3×4+3×6+3×3+3×4+3×5+2××3×4=138(cm2).
(2)【解析】 由三视图知,棱长为2的正方体内接于球,故正方体的体对角线长为2,即为球的直径长.所以球的表面积为S=4π·=12π.
【答案】 12π
考向3 空间几何体的体积
空间几何体的体积公式
几何体名称
体 积
棱(圆)柱
V=Sh(S为底面面积,h为高)
棱(圆)锥
V=Sh(S为底面面积,h为高)
棱(圆)台
V=(S′++S)h
(S′,S为上、下底面面积,h为高)
球
V=R3(R为球半径)
(1)(2014·课标Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
A. B. C. D.
(2)(2014·陕西,5)已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
A. B.4π C.2π D.
【思路导引】 解题(1)时先根据三视图判断出几何体的结构特征,再由体积公式计算;解题(2)的关键是弄清楚球的直径等于正四棱柱的体对角线.
【解析】 (1)由三视图可知,该零件是由两个圆柱组合而成,两个圆柱的体积之和V′=V1+V2=π×22×4+π×32×2=34π.底面半径为3 cm,高为6 cm的圆柱体毛坯的体积V=π×32×6=54π,所以切削掉部分的体积为54π-34π=20π,故切削掉部分的体积与原来毛坯体积的比值为=,故
选C.
(2)依题意可知,正四棱柱体对角线的长度等于球的直径,可设球半径为R,则2R==2,解得R=1,所以V=R3=.
【答案】 (1)C (2)D
求几何体体积的类型及思路
(1)若所给定的几何体是柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用等积转换法或割补法进行求解.其中,等积转换法多用来求锥体的体积.
(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.
(1)(2014·辽宁,7)某几何体三视图如图所示,则该几何体的体积为( )
A.8-2π B.8-π
C.8- D.8-
(2)(2014·江苏,8)设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是________.
(1)【答案】 B 由三视图知,原几何体是棱长为2的正方体挖去两个底面半径为1,高为2的四分之一圆柱,故几何体的体积为8-2×π×2×=8-π.
(2)【解析】 设甲、乙两个圆柱的底面半径和高分别为r1、h1,r2、h2,由侧面积相等,即2πr1h1=2πr2h2,得=.
又==,所以=,
则==·=·==.
【答案】
1.(2014·河南南阳联考,5)已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正(主)视图可能为( )
【答案】 C 由已知条件得直观图如图所示,
正(主)视图是直角三角形,中间的线是看不见的线PA形成的投影,应为虚线,故选C.
2.(2015·山东淄博模拟,4)把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥ABCD的正(主)视图与俯视图如图所示,则其侧(左)视图的面积为( )
A. B.
C. D.
【答案】 D 由正(主)视图与俯视图可得三棱锥ABCD的一个侧面与底面垂直,其侧(左)视图是直角三角形,且直角边长均为,所以侧(左)视图的面积为S=××=.
3.(2015·吉林长春质检,6)某几何体的三视图如图所示,则它的表面积为( )
A.2+π B.2+π
C.2+(1+)π D.2+π
【答案】 A 由几何体的三视图可知,该几何体是经过旋转轴作截面,截取的半个圆锥,底面半径是1,高是2,所以母线长为,所以其表面积为底面半圆面积和圆锥的侧面积的一半以及截面三角形的面积的和,即π+π·+×2×2=π+2,故选A.
4.(2015·河北石家庄调研,8)已知球O,过其球面上A,B,C三点作截面,若O点到该截面的距离是球半径的一半,且AB=BC=2,∠B=120°,则球O的表面积为( )
A. B.
C.4π D.
【答案】 A 由余弦定理,得
AC==2.
设△ABC所在截面圆的半径为r,则2r===4,即r=2.∵O点到截面的距离是球半径的一半,即d=,且d2+r2=R2,∴+4=R2,即R2=.
∴S球=4πR2=4π×=.
5.(2015·安徽蚌埠一模,7)如图所示,用一边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )
A.+ B.+
C. D.+
【答案】 D 蛋巢的底面是边长为1的正方形,所以过四个顶点截鸡蛋所得的截面圆的直径为1.因为鸡蛋的表面积为4π,所以球的半径为1,所以球心到截面的距离d==,而截面到底面的距离即为三角形的高,所以球心到底面的距离为+.
6.(2014·湖北宜昌二模,8)某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )
A.2 B.4 C.8 D.16
【答案】 D 该几何体的直观图如图所示,由直观图可知PA2=102-y2=x2-(2)2,∴x2+y2=128.
又∵128=x2+y2≥2xy,当且仅当x=y时xy取得最大值,
∴此时∴
∴h=PA=6,
∴V=·S△ABC·|PA|=××2×8×6=16.
思路点拨:先根据三视图画出几何体的直观图,找出关于x,y的等量关系,求出当xy取最大时的x,y值,再求体积.
7.(2015·陕西西安模拟,9)已知三棱锥DABC中,AB=BC=1,AD=2,BD=,AC=,BC⊥AD,则该三棱锥的外接球的表面积为( )
A.π B.6π
C.5π D.8π
【答案】 B 由勾股定理,知DA⊥BC,AB⊥BC,
∴BC⊥平面DAB,∴BC⊥BD,
∴CD==.
∴AC2+AD2=2+4=6=CD2,
∴DA⊥AC.
取CD的中点O,由直角三角形的性质知,O到点A,B,C,D的距离均为,
其即为三棱锥的外接球球心.
故三棱锥的外接球的表面积为4π·=6π.
8.(2015·山东临沂模拟,14)四面体ABCD中,共顶点A的三条棱两两相互垂直,且其长分别为2,3,4.若四面体ABCD的四个顶点在同一个球面上,则这个球的表面积为________.
【解析】 依题意,原几何体是一个三棱锥,可以看作一条棱与底面垂直且其长度为3,底面是一个直角三角形,两直角边长分别为2,4,这个几何体可以看作是长、宽、高分别为4,2,3的长方体的一部分,则其外接球的半径为R==,故这个球的表面积为S=4πR2=4π=
29π.
【答案】 29π
9.(2015·山东德州模拟,12)一个几何体的三视图如图所示,其侧视图是一个等边三角形,则这个几何体的体积是________.
【解析】 观察三视图可知,该几何体是圆锥的一半与一个四棱锥的组合体,圆锥底面半径为2,四棱锥底面边长分别为3,4,它们的高均为=2,所以该几何体的体积为×π×22×2+×4×3×2=8+π.
【答案】 π+8
10.(2014·江苏南京二模,8)在四棱锥PABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,PA=2,E为AB的中点,则四面体PBCE的体积为________.
【解析】 由于四边形ABCD是菱形,所以以EB为底边的△CBE的高h=AD·sin 60°=2×=,从而四面体PBCE的体积VPBCE=VCPBE=××1×2×=.
【答案】
思路点拨:求锥体的体积,要选择适当的底面和高,然后应用公式V=Sh进行计算即可.常用方法有割补法、等体积变换法,本题使用了等积变换法.
1.(2015·浙江,13,中)如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是________.
【解析】 如图,连接BM,取BM的中点G,连接NG,AG,
则∠ANG为异面直线AN,CM所成的角.
显然NG=CM=,AN=2.
∵AB=BD,∴BM⊥AD.
在Rt△AMG中,
AG==.
在△ANG中,
cos∠ANG=
==.
【答案】
2.(2015·四川,14,中)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点,设异面直线EM与AF所成的角为θ,则cos θ的最大值为________.
【解析】 设AD=2,QM=m,则0≤m≤2,
以A为坐标原点,建立如图所示的空间直角坐标系.
则E(1,0,0),A(0,0,0),F(2,1,0),M(0,m,2).
∴=(-1,m,2),=(2,1,0),
∴cos θ==
=.
令f(m)=(m∈[0,2]),
易知f(m)在[0,2]上为单调递减函数,
故f(m)max=f(0)=,即cos θ的最大值为.
【答案】
1.(2011·四川,3,易)l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )
A.l1⊥l2,l2⊥l3⇒l1∥l3
B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒ l1,l2,l3共面
D.l1,l2,l3共点⇒l1,l2,l3共面
【答案】 B A项,l1与l3还可能相交或成异面直线,故A错误;B项,∵l2∥l3,l1⊥l2,∴l1⊥l3,故B正确;由三棱柱和三棱锥可知C,D错误,故选B.
2.(2012·四川,6,易)下列命题正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这两个平面平行
【答案】 C 对于选项A,这两条直线可以相交或为异面直线,∴A错误;对于选项B,这两个平面可以相交,∴B错误;对于选项D,这两个平面还可能相交,∴D错误;而由线面平行的性质定理可证C正确.故选C.
3.(2012·重庆,9,中)设四面体的六条棱的长分别为1,1,1,1,和a,且长为a的棱与长为的棱异面,则a的取值范围是( )
A.(0,) B.(0,) C.(1,) D.(1,)
【答案】 A 如图,构造四面体ABCD,使AB=a,CD=,AD=AC=BC=BD=1,取CD的中点E,则AE=BE=,∴+>a,0
0),则C(m,,0),=(m,,0).,
设n1=(x,y,z)为平面ACE的法向量,则
即
可取n1=.
又n2=(1,0,0)为平面DAE的一个法向量,
由题设|cos〈n1,n2〉|=,
即=,解得m=.
因为E为PD的中点,所以三棱锥EACD的高为,三棱锥EACD的体积V=××××=.
1.证明线面平行问题的思路(一)
(1)作(找)出所证线面平行中的平面内的一条直线;
(2)证明线线平行;
(3)根据线面平行的判定定理证明线面平行.
2.证明线面平行问题的思路(二)
(1)在多面体中作出要证线面平行中的线所在的平面;
(2)利用线面平行的判定定理证明所作平面内的两条相交直线分别与所证平面平行;
(3)证明所作平面与所证平面平行;
(4)转化为线面平行.
(2014·安徽,19,13分)如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
解:(1)证明:因为BC∥平面GEFH,BC⊂平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.
同理可证EF∥BC,因此GH∥EF.
(2)如图,连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.
又BD∩AC=O,且AC,BD都在平面ABCD内,所以PO⊥底面ABCD.
又因为平面GEFH⊥平面ABCD,
且PO⊄平面GEFH,
所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,
所以PO∥GK,所以GK⊥平面ABCD,从而GK⊥EF.
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,
从而KB=DB=OB,即K为OB的中点.
再由PO∥GK,得GK=PO,即G是PB的中点,且GH=BC=4.
由已知可得OB=4,PO===6,
所以GK=3.
故四边形GEFH的面积S=·GK=×3=18.
考向2 面面平行的判定与性质
平面与平面平行的判定定理与性质定理
文字语言
图形语言
符号语言
判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为线面平行⇒面面平行)
⇒α∥β
性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行
⇒a∥b
平面与平面平行的性质定理实际上给出了判定两条直线平行的一种方法,注意一定是第三个平面与两平行平面相交,其交线平行.
(2013·江苏,16,14分)如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
【思路导引】 (1)由条件知F为SB中点,EG∥AC,EF∥AB,根据面面平行的判定定理可证平面EFG∥平面ABC;(2)由平面SAB⊥平面SBC,可知AF⊥平面SBC,因此AF⊥BC,再根据已知条件得出BC⊥平面SAB,命题获证.
【证明】 (1)因为AS=AB,AF⊥SB,垂足为F,所以F是SB的中点.又因为E是SA的中点,所以EF∥AB.
因为EF⊄平面ABC,AB⊂平面ABC,
所以EF∥平面ABC.
同理EG∥平面ABC.又EF∩EG=E,
所以平面EFG∥平面ABC.
(2)因为平面SAB⊥平面SBC,且交线为SB,
又AF⊂平面SAB,AF⊥SB,
所以AF⊥平面SBC.
因为BC⊂平面SBC,
所以AF⊥BC.
又因为AB⊥BC,AF∩AB=A,AF,AB⊂平面SAB,
所以BC⊥平面SAB.
因为SA⊂平面SAB,所以BC⊥SA.
1.判定面面平行的四个方法
(1)利用定义:即判断两个平面没有公共点.
(2)利用面面平行的判定定理.
(3)利用垂直于同一条直线的两平面平行.
(4)利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行.
2.平行问题的转化关系
(2013·陕西,18,12分)如图,四棱柱ABCDA1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABDA1B1D1的体积.
解:(1)证明:由题设知,BB1綊DD1,
∴四边形BB1D1D是平行四边形,
∴BD∥B1D1.
又BD⊄平面CD1B1,
∴BD∥平面CD1B1.
∵A1D1綊B1C1綊BC,
∴四边形A1BCD1是平行四边形,
∴A1B∥D1C.
又A1B⊄平面CD1B1,
∴A1B∥平面CD1B1.
又∵BD∩A1B=B,
∴平面A1BD∥平面CD1B1.
(2)∵A1O⊥平面ABCD,
∴A1O是三棱柱ABDA1B1D1的高.
又∵AO=AC=1,AA1=,
∴A1O==1.
又∵S△ABD=××=1,
∴VABDA1B1D1=S△ABD·A1O=1.
思路点拨:解题(1)需将面面平行关系转化为线面平行,再转化为线线平行,通过取特殊四边形来完成证明;解题(2)的关键是选易求高的底面,利用线面垂直的判定找高.
1.(2015·山东潍坊模拟,4)有下列命题:
①若直线l平行于平面α内的无数条直线,则直线l∥α;
②若直线a在平面α外,则a∥α;
③若直线a∥b,b∥α,则a∥α;
④若直线a∥b,b∥α,则a平行于平面α内的无数条直线.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
【答案】 A 命题①直线l可以在平面α内,不正确;命题②直线a与平面α可以是相交关系,不正确;命题③直线a可以在平面α内,不正确;命题④正确.
2.(2014·浙江温州模拟,6)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中错误的是( )
A.若m⊥α,m⊥β,则α∥β
B.若α∥γ,β∥γ,则α∥β
C.若m⊂α,n⊂β,m∥n,则α∥β
D.若m,n是异面直线,m⊂α,m∥β,n⊂β,n∥α,则α∥β
【答案】 C 由线面垂直的性质可知A正确;由两个平面平行的性质可知B正确;由异面直线的性质及面面平行的判定易知D也是正确的;对于选项C,α,β可以相交,可以平行,故C错误,选C.
3.(2015·河南洛阳质检,13)如图,正方体ABCDA1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.
【解析】 因为直线EF∥平面AB1C,EF⊂平面ABCD,且平面AB1C∩平面ABCD=AC,所以EF∥AC.又因为点E是DA的中点,所以F是DC的中点,由中位线定理可得EF=AC.又因为在正方体
ABCDA1B1C1D1中,AB=2,所以AC=2,所以EF=.
【答案】
4.(2015·湖南长沙模拟,18,12分)如图所示,在三棱柱ABCA1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥DBC1C的体积.
解:(1)证明:如图,连接B1C,设B1C与BC1相交于点O,连接OD.
∵四边形BCC1B1是平行四边形,
∴点O为B1C的中点.
又∵D为AC的中点,
∴OD为△AB1C的中位线,
∴OD∥AB1.
又∵OD⊂平面BC1D,AB1⊄平面BC1D,
∴AB1∥平面BC1D.
(2)在三棱柱ABCA1B1C1中,侧棱CC1∥AA1.
又∵AA1⊥平面ABC,
∴侧棱CC1⊥平面ABC.
∴CC1为三棱锥C1BCD的高.
∵D为AC的中点,
∴S△BCD=S△ABC==.
又A1A=CC1=2,
∴VDBCC1=VC1BCD=CC1·S△BCD=×2×=1.
5.(2015·四川成都调研,18,12分)一个多面体的直观图和三视图如图所示,其中M是AB的中点,G是DF上的一动点.
(1)求该多面体的体积与表面积;
(2)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
解:(1)由题中图可知该多面体为直三棱柱,在△ADF中,AD⊥DF,DF=AD=DC=a,所以该多面体的体积为a3,表面积为a2×2+a2+a2+a2=(3+)a2.
(2)点P与点A重合时,GP∥平面FMC.
如图,取FC的中点H,连接GH,GA,MH.
∵G是DF的中点,∴GH綊CD.
又M是AB的中点,∴AM綊CD.
∴GH∥AM且GH=AM,
∴四边形GHMA是平行四边形,
∴GA∥MH.
又∵MH⊂平面FMC,GA⊄平面FMC,
∴GA∥平面FMC,
即当点P与点A重合时,GP∥平面FMC.
6.(2015·河北石家庄模拟,18,12分)如图,棱柱ABCDA1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.
(1)证明:平面AB1C∥平面DA1C1;
(2)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
解:(1)证明:由棱柱ABCDA1B1C1D1的性质,知AB1∥DC1,A1D∥B1C,AB1∩B1C=B1,A1D∩DC1=D,
∴平面AB1C∥平面DA1C1.
(2)存在这样的点P满足题意.
如图,在C1C的延长线上取点P,使C1C=CP,连接BP,
∵B1B綊CC1,∴BB1綊CP,
∴四边形BB1CP为平行四边形,
∴BP∥B1C,
∵A1D∥B1C,
∴BP∥A1D.
又∵A1D⊂平面DA1C1,BP⊄平面DA1C1,
∴BP∥平面DA1C1.
7.(2013·广东惠州调研,19,14分)如图所示,在棱长为2的正方体ABCDA1B1C1D1中,E,F分别为DD1,DB的中点.
(1)求证:EF∥平面ABC1D1;
(2)求证:CF⊥B1E;
(3)求三棱锥B1EFC的体积.
解:(1)证明:如图,连接BD1,在△DD1B中,E,F分别为D1D,DB的中点,
∴EF为△DD1B的中位线,
∴EF∥D1B,
而D1B⊂平面ABC1D1,
EF⊄平面ABC1D1,
∴EF∥平面ABC1D1.
(2)证明:如图,连接B1D1,在等腰直角三角形BCD中,
∵F为BD的中点,
∴CF⊥BD,
在正方体ABCDA1B1C1D1中,
DD1⊥平面ABCD,∵CF⊂平面ABCD,
∴DD1⊥CF,
又DD1∩BD=D,
DD1,BD⊂平面BDD1B1,
∴CF⊥平面BDD1B1,
而B1E⊂平面BDD1B1,
∴CF⊥B1E.
(3)由(2)可知CF⊥平面BDD1B1,
∴CF⊥平面EFB1,即CF为高,CF=BF=.
∵EF=BD1=,B1F===,
B1E===3,
∴EF2+B1F2=B1E2,即∠EFB1=90°,
∴S△B1EF=EF·B1F=,
∴VB1EFC=VCB1EF=·S△B1EF·CF
=××=1.
1.(2015·浙江,8,中)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′CDB的平面角为α,则( )
A.∠A′DB≤α B.∠A′DB≥α
C.∠A′CB≤α D.∠A′CB≥α
【答案】 B 根据二面角的定义,以及折叠过程可知B正确.
2.(2015·重庆,19,13分,中)如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=,D,E分别为线段AB,BC上的点,且CD=DE=,CE=2EB=2.
(1)证明:DE⊥平面PCD;
(2)求二面角APDC的余弦值.
解:(1)证明:由PC⊥平面ABC,DE⊂平面ABC,得PC⊥DE.
由CE=2,CD=DE=得△CDE为等腰直角三角形,故CD⊥DE.
又PC∩CD=C,所以DE⊥平面PCD.
(2)由(1)知,△CDE为等腰直角三角形,∠DCE=.如图,过D作DF垂直CE于F,易知DF=FC=FE=1.
又EB=1,故FB=2.
由∠ACB=得DF∥AC,==,故AC=DF=.
以C为坐标原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0),P(0,0,3),A,E(0,2,0),D(1,1,0),=(1,-1,0),=(-1,-1,3),=.
设平面PAD的法向量为n1=(x1,y1,z1),
由n1·=0,n1·=0,
得
故可取n1=(2,1,1).
由(1)可知,DE⊥平面PCD,
故平面PCD的法向量n2可取为,
即n2=(1,-1,0).
从而法向量n1,n2的夹角的余弦值为
cos〈n1,n2〉==,
故二面角APDC的余弦值为.
3.(2015·湖北,19,12分,中)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马PABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
(1)证明:PB⊥平面DEF,试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为,求的值.
解:方法一:(1)证明:因为PD⊥底面ABCD,所以PD⊥BC,
由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,
所以BC⊥平面PCD.而DE⊂平面PCD,所以BC⊥DE.
又因为PD=CD,点E是PC的中点,
所以DE⊥PC.
PC∩BC=C,所以DE⊥平面PBC,
而PB⊂平面PBC,所以PB⊥DE.
又PB⊥EF,DE∩EF=E,
所以PB⊥平面DEF.
由DE⊥平面PBC,PB⊥平面DEF,可知四面体DBEF的四个面都是直角三角形,即四面体DBEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.
(2)如图,在面PBC内,延长BC与FE的延长线交于点G,则DG是平面DEF与平面ABCD的交线.由(1)知,PB⊥平面DEF,所以PB⊥DG.
又因为PD⊥底面ABCD,所以PD⊥DG,而PD∩PB=P,所以DG⊥平面PBD.
故∠BDF是面DEF与面ABCD所成二面角的平面角,
设PD=DC=1,BC=λ,有BD=,
在Rt△PDB中,由DF⊥PB,得∠DPF=∠FDB=,
则tan=tan∠DPF===,解得λ=.
所以==.
故当面DEF与面ABCD所成二面角的大小为时,=.
方法二:(1)证明:如图,以D为原点,射线DA,DC,DP分别为x轴,y轴,z轴的正半轴,建立空间直角坐标系,设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),=(λ,1,-1),
点E是PC的中点,所以E,=,
于是·=0,即PB⊥DE.
又已知EF⊥PB,而DE∩EF=E,所以PB⊥平面DEF.
因为=(0,1,-1),·=0,则DE⊥PC,所以DE⊥平面PBC.
由DE⊥平面PBC,PB⊥平面DEF,可知四面体DBEF的四个面都是直角三角形,即四面体DBEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.
(2)由PD⊥平面ABCD,所以=(0,0,1)是平面ABCD的一个法向量.
由(1)知,PB⊥平面DEF,所以=(-λ,-1,1)是平面DEF的一个法向量.
若面DEF与面ABCD所成二面角的大小为,
则cos=
==.
解得λ=,所以==.
故当面DEF与面ABCD所成二面角的大小为时,=.
1.(2011·浙江,4,中)下列命题中错误的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
【答案】 D 对于命题A,在平面α内存在直线l平行于平面α与平面β的交线,则l平行于平面β,故命题A正确.
对于命题B,若平面α内存在直线垂直于平面β,则平面α与平面β垂直,故命题B正确.
对于命题C,设α∩γ=m,β∩γ=n,在平面γ内取一点P不在l上,过P作直线a,b,使a⊥m,b⊥n.∵γ⊥α,a⊥m,则a⊥α,∴a⊥l,同理有b⊥l.又a∩b=P,a⊂γ,b⊂γ,∴l⊥γ.故命题C
正确.
对于命题D,设α∩β=l,则l⊂α且l⊂β.故在α内存在直线不垂直于平面β,即命题D错误,故
选D.
2.(2012·浙江,10,难)已知矩形ABCD,AB=1,BC=,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三对直线“AC与BD”“AB与CD”“AD与BC”均不垂直
【答案】 B 若存在某个位置,使得AC⊥BD,作AE⊥BD于E,如图,则BD⊥平面AEC,所以BD⊥EC.在△ABD中,AB2=BE·BD,BE=,而在△BCD中,BC2=BE·BD,BE=,两者矛盾.故A错误.
若存在某个位置,使得AB⊥CD,又因为AB⊥AD,则AB⊥平面ACD,所以AB⊥AC,即AC=1,故B正确,D错误.
若存在某个位置,使得AD⊥BC,又因为AD⊥AB,则AD⊥平面ABC,所以AD⊥AC,而斜边CD小于直角边AD,矛盾,故C错误.
3.(2014·福建,17,13分,中)在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
解:(1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,AB⊥BD,∴AB⊥平面BCD.
又CD⊂平面BCD,∴AB⊥CD.
(2)过点B在平面BCD内作BE⊥BD,如图.
由(1)知AB⊥平面BCD,BE⊂平面BCD,BD⊂平面BCD,
∴AB⊥BE,AB⊥BD.
以B为坐标原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系.
依题意,得B(0,0,0),C(1,1,0),D(0,1,0),A(0,0,1),M,
则=(1,1,0),=,
=(0,1,-1).
设平面MBC的法向量n=(x0,y0,z0),
则
即
取z0=1,得平面MBC的一个法向量n=(1,-1,1).
设直线AD与平面MBC所成角为θ,
则sin θ=|cos〈n,〉|==,
即直线AD与平面MBC所成角的正弦值为.
4.(2013·广东,18,12分,中)如图①,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=,O为BC的中点.将△ADE沿DE折起,得到如图②所示的四棱锥A′BCDE,其中A′O=.
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′CDB的平面角的余弦值.
解:(1)证明:在题干图①中,易得OC=3,AC=3,AD=2,连接OD,OE.
在△OCD中,由余弦定理可得
OD=
=,
由翻折不变性可知A′D=2,
所以A′O2+OD2=A′D2,所以A′O⊥OD,
同理可证A′O⊥OE,又OD∩OE=O,
所以A′O⊥平面BCDE.
(2)如图,过O作OH⊥CD交CD的延长线于H,连接A′H,
因为A′O⊥平面BCDE,所以A′O⊥CD,
又OH⊥CD,OH∩A′O=O,
所以CD⊥平面A′OH,所以A′H⊥CD,
所以∠A′HO为二面角A′CDB的平面角.
结合题图①可知,△ABC为等腰直角三角形,又OH⊥CD,所以H为AC的中点,又BC=6,故OH=,
从而A′H==,
所以cos∠A′HO==,所以二面角A′CDB的平面角的余弦值为.
5.(2014·湖南,19,12分,中)如图,四棱柱ABCDA1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
解:(1)证明:因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD.因为CC1∥DD1,所以CC1⊥BD.
而AC∩BD=O,因此CC1⊥底面ABCD.
由题设知,O1O∥C1C,故O1O⊥底面ABCD.
(2)方法一:如图①,过O1作O1H⊥OB1于H,连接HC1.
由(1)知,O1O⊥底面ABCD,所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.
又因为四棱柱ABCDA1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形,因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1,进而OB1⊥C1H.故∠C1HO1是二面角C1OB1D的平面角.
不妨设AB=2.
因为∠CBA=60°,
所以OB=,OC=1,OB1=.
在Rt△OO1B1中,
易知O1H==2.
而O1C1=1,于是
C1H===.
故cos∠C1HO1===.
即二面角C1OB1D的余弦值为.
方法二:因为四棱柱ABCDA1B1C1D1的所有棱长都相等,所以四边形ABCD是菱形,因此AC⊥BD.
又O1O⊥底面ABCD,
从而OB,OC,OO1两两垂直.
如图②,以O为坐标原点,OB,OC,OO1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Oxyz.不妨设AB=2.
因为∠CBA=60°,所以OB=,OC=1,
于是相关各点的坐标为O(0,0,0),B1(,0,2),C1(0,1,2).
=(,0,2),=(0,1,2).
易知,n1=(0,1,0)是平面BDD1B1的一个法向量.
设n2=(x,y,z)是平面OB1C1的一个法向量,
则即
取z=-,则x=2,y=2 ,
所以n2=(2,2 ,-).
设二面角C1OB1D的大小为θ,易知θ是锐角,于是cos θ=|cos〈n1,n2〉|
===.
故二面角C1OB1D的余弦值为.
6.(2013·辽宁,18,12分,中)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.
解:(1)证明:由AB是圆的直径,得AC⊥BC,由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.
又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.
因为BC⊂平面PBC,
所以平面PBC⊥平面PAC.
(2)方法一:过C作CM⊥AB于M,
因为PA⊥平面ABC,CM⊂平面ABC,
所以PA⊥CM,
故CM⊥平面PAB.
过M作MN⊥PB于N,连接NC,
由三垂线定理得CN⊥PB.
所以∠CNM为二面角CPBA的平面角.
在Rt△ABC中,由AB=2,AC=1,得BC=,CM=,BM=.
在Rt△PAB中,由AB=2,PA=1,得PB=.
因为Rt△BMN∽Rt△BPA,
所以=,故MN=.
又在Rt△CNM中,CN=,
故cos∠CNM=.
所以二面角CPBA的余弦值为.
方法二:过C作CM∥AP,则CM⊥平面ABC.
如图,以点C为坐标原点,以CB,CA,CM所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
因为AB=2,AC=1,所以BC=.
因为PA=1,所以A(0,1,0),B(,0,0),P(0,1,1),
故=(,0,0),=(0,1,1).
设平面BCP的法向量为n1=(x,y,z),
则
所以
不妨令y=1,则n1=(0,1,-1).
因为=(0,0,1),=(,-1,0),
设平面ABP的法向量为n2=(x,y,z),
则所以
不妨令x=1,则n2=(1,,0).
于是cosn1,n2==,
所以二面角CPBA的余弦值为.
考向1 线面垂直的判定与性质
直线与平面垂直的判定定理及性质定理
文字语言
图形语言
符号语言
判定定理
一条直线与平面内的两条相交直线都垂直,则该直线与此平面垂直
⇒l⊥α
性质定理
垂直于同一个平面的两条直线平行
⇒a∥b
(2014·重庆,20,12分)如图,四棱锥PABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=,M为BC上一点,且BM=.
(1)证明:BC⊥平面POM;
(2)若MP⊥AP,求四棱锥PABMO的体积.
【思路导引】 (1)先得出OM⊥BM,再由线面垂直的性质得PO⊥BC,从而利用线面垂直的判定定理得出结论;(2)设PO=a,利用图形中的直角三角形和余弦定理得到关于a的等式,求解出棱锥的高,从而求解出几何体的体积.
【解析】 (1)证明:如图,因为四边形ABCD为菱形,O为菱形中心,连接OB,则AO⊥OB.因为∠BAD=,故OB=AB·sin∠OAB=2sin=1.
又因为BM=,且∠OBM=,在△OBM中,
OM2=OB2+BM2-2OB·BM·cos∠OBM
=12+-2×1××cos =.
所以OB2=OM2+BM2,故OM⊥BM.
又PO⊥底面ABCD,且BD⊂平面ABCD,所以PO⊥BC.从而BC与平面POM内两条相交直线OM,PO都垂直,所以BC⊥平面POM.
(2)由(1)可得,OA=AB·cos∠OAB=2×cos=.
设PO=a,由PO⊥底面ABCD知,△POA,△POM均为直角三角形,故PA2=PO2+OA2=a2+3,
PM2=PO2+OM2=a2+.
连接AM,在△ABM中,AM2=AB2+BM2-2AB·BM·cos∠ABM=22+-2×2××cos =.
由已知MP⊥AP,故△APM为直角三角形,则PA2+PM2=AM2,即a2+3+a2+=,得a=,a=-(舍去),即PO=.
此时,S四边形ABMO=S△AOB+S△OMB=·AO·OB+·BM·OM=××1+××=.
所以四棱锥PABMO的体积
VPABMO=·S四边形ABMO·PO=××=.
1.证明直线与平面垂直的具体步骤
(1)找与作:在已知平面内找或作两条相交直线与已知直线垂直;
(2)证:证明所找到的或所作的直线与已知直线垂直;
(3)用:利用线面垂直的判定定理,得出结论.
2.判定线面垂直的四种方法
(1)利用线面垂直的判定定理.
(2)利用“两平行线中的一条与已知平面垂直,则另一条也与这个平面垂直”.
(3)利用“一条直线垂直于两平行平面中的一个,则与另一个也垂直”.
(4)利用面面垂直的性质定理.
(2011·辽宁,18,12分)如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.
(1)证明:PQ⊥平面DCQ;
(2)求棱锥QABCD的体积与棱锥PDCQ的体积的比值.
解:(1)证明:由条件知四边形PDAQ为直角梯形,
因为QA⊥平面ABCD,QA⊂平面PDAQ,
所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ,
又PQ⊂平面PDAQ,所以PQ⊥DC.
在直角梯形PDAQ中可得
DQ=PQ=PD,则PQ⊥DQ.
又DC∩QD=D,
所以PQ⊥平面DCQ.
(2)设AB=a.由题设知AQ为棱锥QABCD的高,
所以棱锥QABCD的体积V1=a3.
由(1)知PQ为棱锥PDCQ的高,
而PQ=a,△DCQ的面积为a2,
所以棱锥PDCQ的体积V2=a3.
故棱锥QABCD的体积与棱锥PDCQ的体积的比值为1.
考向2 面面垂直的判定与性质
平面与平面垂直的判定定理及性质定理
文字语言
图形语言
符号语言
判定定理
一个平面过另一个平面的一条垂线,则这两个平面互相垂直
⇒α⊥β
性质定理
两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面
⇒l⊥α
(2013·北京,17,14分)如图,在四棱锥PABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点.求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
【思路导引】 解题(1)的关键是利用面面垂直的性质进行转化;解题(2)的关键是寻找线线平行;解题(3)的关键是准确寻找垂线,可利用题目中的垂直关系来寻找.
【证明】 (1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,
E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.
所以BE∥AD.
又因为BE⊄平面PAD,AD⊂平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且四边形ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD.
所以PA⊥CD.
所以CD⊥平面PAD.
所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.
所以CD⊥EF.
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
1.面面垂直的证明的两种思路
(1)用面面垂直的判定定理,即证明其中一个平面经过另一个平面的一条垂线;
(2)用面面垂直的定义,即证明两个平面所成的二面角是直二面角,把证明面面垂直的问题转化为证明平面角为直角的问题.
2.垂直问题的转化关系
(2012·课标全国,19,12分)如图,三棱柱ABCA1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC;
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
解:(1)证明:由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C,所以BC⊥平面ACC1A1.
又DC1⊂平面ACC1A1,所以DC1⊥BC.
由题设知∠A1DC1=∠ADC=45°,所以∠CDC1=90°,即DC1⊥DC.
又DC∩BC=C,所以DC1⊥平面BDC.
又DC1⊂平面BDC1,故平面BDC1⊥平面BDC.
(2)设棱锥BDACC1的体积为V1,AC=1.
由题意得V1=××1×1=.
又三棱柱ABCA1B1C1的体积V=1,所以(V-V1)∶V1=1∶1.
故平面BDC1分此棱柱所得两部分体积的比为1∶1.
考向3 线面角、二面角的求法
1.线面角
(1)当l⊥α时,线面角为90°.
(2)当l∥α或l⊂α时,线面角为0°.
(3)线面角θ的范围:0°≤θ≤90°.
2.二面角
(1)如图所示的二面角αlβ,若①O∈l,②OA⊂α,OB⊂β,③OA⊥l,OB⊥l,则∠AOB就叫作二面角αlβ的平面角.
(2)二面角θ的范围:0°≤θ≤180°.
(1)(2013·山东,4)已知三棱柱ABCA1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
A. B. C. D.
(2)(2014·浙江,20,15分)如图,在四棱锥ABCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,
AC=.
①证明:DE⊥平面ACD;
②求二面角BADE的大小.
【思路导引】 (1)先取上底面的中心P′,连接PP′,则PP′⊥平面ABC,∠PAP′为所求,然后在△PAP′中求解;
(2)①证明DE⊥AC,DE⊥DC,然后根据线面垂直的判定定理证明;
②方法一:利用几何法,先根据线面垂直,作出二面角的平面角,然后在直角三角形中求解.
方法二:利用代数法(向量法),先建立空间直角坐标系,然后求出所涉及平面的法向量的夹角,最后结合图形求出二面角的平面角.
【解析】 (1)如图所示,过P作PP′⊥平面ABC于P′,则P′为平面ABC的中心.连接AP′,延长交BC于点M.
则∠P′AP即为PA与平面ABC所成的角.
由V=Sh,
得h===,
即PP′=.
又AP′=AM=1,
∴tan∠P′AP=,
∴∠P′AP=,故选B.
(2)①证明:由题意知四边形BCDE为直角梯形.在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=.
由AC=,AB=2,得AB2=AC2+BC2,即AC⊥BC.
又平面ABC⊥平面BCDE,
从而AC⊥平面BCDE.
所以AC⊥DE.又DE⊥DC,从而DE⊥平面ACD.
②方法一:如图,作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG,
由(1)知DE⊥AD,则FG⊥AD.
所以∠BFG是二面角BADE的平面角.
在直角梯形BCDE中,
由CD2=BC2+BD2,得BD⊥BC.
又平面ABC⊥平面BCDE,
得BD⊥平面ABC,从而BD⊥AB.
由于AC⊥平面BCDE,得AC⊥CD.
在Rt△ACD中,
由DC=2,AC=,得AD=.
在Rt△AED中,
由ED=1,AD=,得AE=.
在Rt△ABD中,由BD=,AB=2,AD=,
得BF=,AF==AD,
从而GF=.
在△ABE,△ABG中,利用余弦定理分别可得cos∠BAE=,BG=.
在△BFG中,cos∠BFG==.
所以∠BFG=,
即二面角BADE的大小是.
方法二:以D为原点,分别以射线DE,DC为x,y轴的正半轴,建立空间直角坐标系Dxyz,如图所示,
由题意知各点坐标如下:
D(0,0,0),E(1,0,0),C(0,2,0),A(0,2,),B(1,1,0).
设平面ADE的法向量为m=(x1,y1,z1),平面ABD的法向量为n=(x2,y2,z2).
可算得=(0,-2,-),=(1,-2,-),=(1,1,0),
由
得
可取m=(0,1,-).
由得
可取n=(1,-1,).
于是|cos〈m,n〉|===.
由题意可知,所求二面角是锐角,
故二面角BADE的大小是.
1.求空间角的方法
(1)几何法;(2)代数法(向量法).
2.用几何法求空间角的三个步骤
(1)找:即找出相关的角;
(2)证:即证明找出的角即为所求的角;
(3)计算:即通过解三角形的方法求出所求角.
3.空间角的找法
(1)线面角
找出斜线在平面上的射影,关键是作出垂线,确定垂足.
(2)二面角
二面角的大小用它的平面角来度量,平面角的常见作法有:①定义法;②垂面法.其中定义法是最常用的方法.
(2014·广东,18,13分)如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
解:(1)∵PD⊥平面ABCD,AD⊂平面ABCD,
∴PD⊥AD,又AD⊥CD,
PD∩CD=D,
∴AD⊥平面PCD.
又PC⊂平面PCD,
∴AD⊥PC.
又AF⊥PC,AD∩AF=A,
∴PC⊥平面ADF,
即CF⊥平面ADF.
(2)方法一:如图所示,分别过点E作EG⊥AF于G,EH⊥DF于H,连接GH,不妨设正方形ABCD边长为1,则DF=,DE=,EF=,EH==.
∴AE==,
AF==.
又CD⊥PD,CD⊥AD,PD∩AD=D,
∴CD⊥平面AED.
∵FE∥CD,
∴FE⊥平面AED.
∴FE⊥AE,
∴EG==.
又AD⊥平面PCD,∴AD⊥EH.
又EH⊥DF,AD∩DF=D,
∴EH⊥平面ADF,
∴EH⊥AF,
∴AF⊥平面EGH.
∴∠EGH即为平面ADF和平面AEF所成的二面角,
又sin∠EGH==,
∴cos∠EGH
==.
方法二:不妨设正方形ABCD的边长为1.建立如图所示的空间直角坐标系.
则D(0,0,0),A(0,0,1),C(0,1,0),
由(1)知CF⊥DF,从而∠CDF=∠DPC=30°,
所以CF=,DF=,
又FE∥CD,∴==,
∴DE=,
同理,EF=CD=,
由此得F,E,
P(,0,0).
设平面AFE的法向量为n=(x,y,z),=,=,
可得
令x=4,则y=0,z=,∴n=(4,0,).
而平面ADF的一个法向量为=,
∴cos〈,n〉===,
由图知二面角DAFE的余弦值为.
1.(2015·皖西七校联考,4)已知α,β是两个不同的平面,下列四个条件中能推出α∥β的是( )
①存在一条直线a,a⊥α,a⊥β;
②存在一个平面γ,γ⊥α,γ⊥β;
③存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α;
④存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α.
A.①③ B.②④ C.①④ D.②③
【答案】 C 对于①,垂直于同一直线的两个平面平行,故当a⊥α,a⊥β时,α∥β,①正确;
对于②,若γ⊥α,γ⊥β,α与β可能平行,也可能相交,此时α,β的交线与γ垂直,②不正确;
若a⊂α,b⊂β,a∥β,b∥α,则α与β可能平行,也可能相交,此时a,b均与α,β的交线平行,③不正确;对于④,存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α.则可在β内作a的平行线c,且c与b相交,则有相交直线b,c都与平面α平行,根据面面平行的判定定理,可得④正确.
2.(2014·河南安阳调研,5)设a,b是不同的直线,α,β是不同的平面,则下列命题:
①若a⊥b,a⊥α,则b∥α;
②若a∥α,α⊥β则a⊥β;
③若a⊥β,α⊥β,则a∥α;
④若a⊥b,b⊥β,则a⊥β.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
【答案】 A 对①,直线b有可能在平面α内;对②,a可能平行于β,也可能在β内;对③,a可能在α内;对④,a可能平行于β,也可能在β内,不可能与β垂直,综上可知没有正确的,故选A.
3.(2015·山西太原二模,13)设α,β,γ为互不重合的三个平面,l为直线,给出下列命题:
①若α∥β,α⊥γ,则β⊥γ;
②若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ;
③若直线l与平面α内的无数条直线垂直,则直线l与平面α垂直;
④若α内存在不共线的三点到β的距离相等,则平面α平行于平面β.
其中真命题的序号为________(写出所有真命题的序号).
【解析】 借助于正方体易知①②正确;对于③,若平面α内与直线l垂直的无数条直线都平行,则直线l可能与平面α不垂直,所以③错;④中的不共线的三点有可能是在平面β的两侧,所以两个平面可能相交或平行,所以④错,故填①②.
【答案】 ①②
4.(2015·河北保定模拟,14)在直二面角αMNβ中,等腰直角三角形ABC的斜边BC⊂α,一直角边AC⊂β,BC与β所成角的正弦值为,则AB与β所成的角是________.
【解析】 如图所示,作BH⊥MN于点H,连接AH,
则BH⊥β,∠BCH为BC与β所成的角.
∵sin∠BCH==,设BC=1,则BH=.
∵△ABC为等腰直角三角形,∴AC=AB=,
∴AB与β所成的角为∠BAH.
∴sin∠BAH===,
∴∠BAH=.
【答案】
5.(2015·江苏徐州模拟,17,14分)如图,在直三棱柱ABCA1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不与点C重合),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
证明:(1)因为ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.
又AD⊂平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE⊂平面BCC1B1,CC1∩DE=E,
所以AD⊥平面BCC1B1.
又AD⊂平面ADE,
所以平面ADE⊥平面BCC1B1.
(2)连接DF,图略.由(1)知AD⊥平面BCC1B1,∵BC⊂平面BCC1B1,
∴AD⊥BC.
又∵AB=AC,∴D为BC的中点,
∴DF綊A1A,∴四边形ADFA1为平行四边形,∴A1F∥AD.
又∵AD⊂平面ADE,
∴A1F∥平面ADE.
6.(2015·福建福州一模,19,13分)如图,三棱锥ABCD中,AB⊥平面BCD,CD⊥BD.
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥AMBC的体积.
解:(1)证明:∵AB⊥平面BCD,CD⊂平面BCD,∴AB⊥CD.
又∵CD⊥BD,AB∩BD=B,
AB⊂平面ABD,BD⊂平面ABD,
∴CD⊥平面ABD.
(2)方法一:由AB⊥平面BCD,得AB⊥BD.
∵AB=BD=1,∴S△ABD=.
∵M是AD的中点,
∴S△ABM=S△ABD=.
由(1)知,CD⊥平面ABD,
∴三棱锥CABM的高h=CD=1,
因此三棱锥AMBC的体积
VAMBC=VCABM=S△ABM·h=.
方法二:由AB⊥平面BCD,知平面ABD⊥平面BCD.
又平面ABD∩平面BCD=BD,
如图,过点M作MN⊥BD,交BD于点N,
则MN⊥平面BCD,且MN=AB=.
又CD⊥BD,BD=CD=1,
∴S△BCD=.
∴三棱锥AMBC的体积
VAMBC=VABCD-VMBCD
=AB·S△BCD-MN·S△BCD
=.
方法点拨:求解此类问题应过好两关:第一关,线面垂直证明关,常利用线面垂直的判定定理证明;第二关,常利用“等体积法”求棱锥的体积.
7.(2015·山东青岛质检,17,12分)如图,在直四棱柱ABCDA1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥平面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.
解:(1)证明:由直四棱柱ABCDA1B1C1D1,得BB1∥DD1,BB1=DD1,
∴BB1D1D是平行四边形,∴B1D1∥BD.
∵BD⊂平面A1BD,B1D1⊄平面A1BD,
∴B1D1∥平面A1BD.
(2)证明:∵BB1⊥平面ABCD,AC⊂平面ABCD,∴BB1⊥AC.
又∵BD⊥AC,且BD∩BB1=B,
∴AC⊥平面BB1D1D.
∵MD⊂平面BB1D1D,∴MD⊥AC.
(3)当点M为棱BB1的中点时,平面DMC1⊥平面CC1D1D.证明如下:
取DC的中点N,D1C1的中点N1,连接NN1交DC1于O,连接OM,如图所示.
∵N是DC的中点,BD=BC,
∴BN⊥DC.
又∵DC是平面ABCD与平面DCC1D1的交线,平面ABCD⊥平面DCC1D1,
∴BN⊥平面DCC1D1.
由题意可得O是NN1的中点,
∴BM∥ON且BM=ON,
即四边形BMON是平行四边形.
∴BN∥OM.
∴OM⊥平面CC1D1D.
∵OM⊂平面DMC1,
∴平面DMC1⊥平面CC1D1D.
8.(2015·四川成都调研,18,12分)如图,四棱锥PABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
(1)证明:PA⊥BD;
(2)若PD=AD,求二面角APBC的余弦值.
解:(1)证明:因为∠DAB=60°,AB=2AD=2,由余弦定理得BD=.
从而BD2+AD2=AB2,
∴BD⊥AD.
∵PD⊥平面ABCD,BD⊂平面ABCD,
∴PD⊥BD.
又AD∩PD=D,
所以BD⊥平面PAD,
所以PA⊥BD.
(2)如图,以D为坐标原点,DA,DB,DP分别为x,y,z的正半轴建立空间直角坐标系Dxyz.
则A(1,0,0),B(0,,0),C(-1,,0),P(0,0,1),=(-1,,0),=(0,,-1),=(-1,0,0),
设平面PAB的法向量为n=(x,y,z),
则
即
因此,令y=1,则n=(,1,).
设平面PBC的法向量为m=(x0,y0,z0),则
即
可取m=(0,1,),
则cos〈m,n〉===,
由图知二面角APBC为钝角,故二面角APBC的余弦值为-.