浙江专用2021届高考数学一轮复习第五章三角函数与解三角形5-4解三角形及其综合应用课件

浙江专用2021届高考数学一轮复习第五章三角函数与解三角形5-4解三角形及其综合应用课件

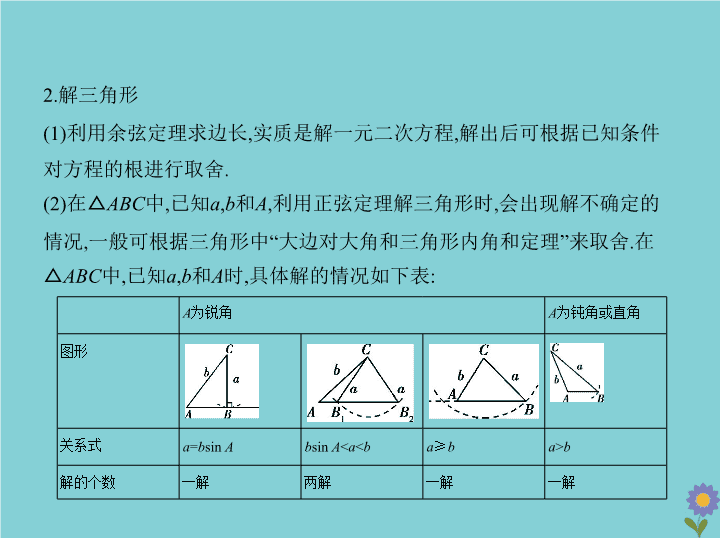
§５.４ 解三角形及其综合应用 高考数学 考点一　正弦定理和余弦定理 1.正弦定理和余弦定理 正弦定理 余弦定理 内容   =   =   =2 R ( R 为△ ABC 外接圆半径) a 2 = b 2 + c 2 -2 bc ·cos Ab 2 = c 2 + a 2 -2 ca ·cos Bc 2 =①      a 2 + b 2 -2 ab ·cos C      考点 清单 变形 形式 (1) a =2 R sin A , b =2 R sin B , c =2 R sin C ; (2)sin A =   ,sin B =   ,sin C =   ; (3) a ∶ b ∶ c =②     sin A ∶sin B ∶sin C      ; (4)   =③             =④ 　2 R      cos A =   ; cos B =   ; cos C =   解决的问题 (1)已知两角和任意一边,求另一角和其他两条边; (2)已知两边和其中一边的对角,求另一边和其他两角 (1)已知三边,求各角; (2)已知两边和它们的夹角,求第三边和其他两个角 2.解三角形 (1)利用余弦定理求边长,实质是解一元二次方程,解出后可根据已知条件 对方程的根进行取舍. (2)在△ ABC 中,已知 a , b 和 A ,利用正弦定理解三角形时,会出现解不确定的 情况,一般可根据三角形中“大边对大角和三角形内角和定理”来取舍.在 △ ABC 中,已知 a , b 和 A 时,具体解的情况如下表: A 为锐角 A 为钝角或直角 图形         关系式 a = b sin A b sin A < a < b a ≥ b a > b 解的个数 一解 两解 一解 一解 　　上表中,若 A 为锐角,则当 a < b sin A 时无解;若 A 为钝角或直角,则当 a ≤ b 时无解. 3.三角形中常用的结论 在△ ABC 中,角 A , B , C 所对的边分别是 a , b , c ,常见的结论有: (1) A + B + C =π; (2)在△ ABC 中,大角对大边,大边对大角,如: a > b ⇔ A > B ⇔ sin A >sin B ; (3)任意两边之和大于第三边,任意两边之差小于第三边; (4)在锐角三角形 ABC 中,sin A >cos B ⇔ A + B >   ; (5)在斜△ ABC 中,tan A +tan B +tan C =tan A ·tan B ·tan C ; (6)有关三角形内角的常用三角恒等式:sin( A + B )=sin C ;cos( A + B )=-cos C ;tan ( A + B )=-tan C   ;sin   =cos   ;cos   =sin   . 考点二　解三角形及其综合应用 1.实际问题中的常用术语 术语 名称 术语意义 图形表示 仰角与俯角 在目标视线与水平视线所成的 角中,目标视线在水平视线上方 的角叫做仰角,目标视线在水平 视线下方的角叫做俯角   方位角 从某点的指北方向线起按顺时 针方向到目标方向线之间的水 平夹角叫做方位角.方位角 α 范 围是0 ° ≤ α <360 °   方向角 正北或正南方向线与目标方向 线所成的锐角,通常表达为北 (南)偏东(西) ×× 度 北偏东 m °   坡角 坡面与水平面的夹角 设坡角为 α ,坡度为 i ,则 i =   =tan α   坡度 坡面的垂直高度 h 和水平宽度 l 的比 2.实际测量中的常见问题 求 AB 图形 需要测量 的元素 解法       ∠ ACB = α , BC = a 解直角三角形 AB = a tan α     ∠ ACB = α , ∠ ADB = β , CD = a 解两个直角三角 形 AB =         ∠ ACB = α , AC = b , BC = a 用余弦定理 AB =       ∠ ACB = α , ∠ ABC = β , CB = a 用正弦定理 AB =       ∠ ADC = α , ∠ BDC = β , ∠ BCD = δ , ∠ ACD = γ , CD = a 在△ ADC 中, AC =   ; 在△ BCD 中, BC =   ; 在△ ABC 中,应用 余弦定理求 AB 3.三角形的面积公式 (1)已知三角形一边及该边上的高,利用 S =   ah ( h 表示边 a 上的高); (2)已知三角形的两边及其夹角,利用 S =   ab sin C   S =   ac sin B , S =   bc sin A   . 知识拓展　(1)已知三角形的三边,利用 S =     ; (2)已知三角形的三边及内切圆半径,利用 S =   ( a + b + c ) r ( r 为三角形的内切圆 半径). (3) S =   =2 R 2 sin A sin B sin C ( R 为△ ABC 外接圆的半径). 考法一 　利用正、余弦定理解三角形 知能拓展 例1 　(1)在△ ABC 中,分别根据所给条件指出解的个数. ① a =4, b =5, A =30 ° ; ② a =5, b =4, A =60 ° ; ③ a =   , b =   , B =120 ° ; ④ a =   , b =   , A =60 ° . (2)(2017课标全国Ⅲ,17,12分)△ ABC 的内角 A , B , C 的对边分别为 a , b , c .已知 sin A +   cos A =0, a =2   , b =2. ①求 c ; ②设 D 为 BC 边上一点,且 AD ⊥ AC ,求△ ABD 的面积. 解析 　(1)①∵ a < b , b sin A =   <4,∴有两解. ②∵ a > b , A <90 ° ,∴ B < A ,∴有一解.③∵ B >90 ° , a > b ,∴无解. ④∵ a < b , b sin A =   ×   =     .∴ a < b sin A < b ,∴无解. (2)①由已知可得tan A =-   ,所以 A =   .在△ ABC 中,由余弦定理得28=4+ c 2 -4 c cos   ,即 c 2 +2 c -24=0.解得 c =-6(舍去)或 c =4. ②由题设可得∠ CAD =  ， 所以∠ BAD =∠ BAC -∠ CAD =   . 故△ ABD 面积与△ ACD 面积的比值为   =1. 又△ ABC 的面积为   × 4 × 2sin∠ BAC =2   ,所以△ ABD 的面积为   . 方法总结 　1.已知两角 A 、 B 与一边 a ,由 A + B + C =π及   =   =   ,可先 求出角 C ,再求出 b 、 c . 2.已知两边 b 、 c 及其夹角 A ,由 a 2 = b 2 + c 2 -2 bc cos A ,先求出 a ,再由正弦定理求 出角 B 、 C . 3.已知三边 a 、 b 、 c ,由余弦定理可求出角 A 、 B 、 C . 4.已知两边 a 、 b 及其中一边 a 的对角 A ,由   =   可求出另一边 b 的对角 B ,由 C =π-( A + B )可求出 C ,再由   =   可求出 c ,而通过   =   求 B 时, 可能有一解、两解或无解的情况. 考法二 　三角形形状的判断 例2     (2019豫北名校1月联考,8)在△ ABC 中, a , b , c 分别表示三个内角 A , B , C 的对边,如果( a 2 + b 2 )sin( A - B )=( a 2 - b 2 )·sin( A + B ),则△ ABC 的形状为   (　　) A.等腰三角形　    B.直角三角形 C.等腰直角三角形　    D.等腰三角形或直角三角形 解题导引　 解法一:首先对原式进行化简,然后利用正弦定理把边化成角, 从而判断三角形的形状. 解法二:首先对原式进行化简,然后利用正、余弦定理把角化成边,从而判 断三角形的形状. 解析 　解法一:已知等式可化为 a 2 [sin( A - B )-sin( A + B )]= b 2 [-sin( A + B )-sin( A - B )],∴2 a 2 cos A sin B =2 b 2 cos B sin A .由正弦定理,得sin 2 A cos A sin B =sin 2 B cos B sin A ,∴sin A sin B (sin A cos A -sin B cos B )=0, ∵ A , B 均为△ ABC 的内角,∴sin A ≠ 0,sin B ≠ 0, ∴sin 2 A -sin 2 B =0,即sin 2 A =sin 2 B . 由 A , B ∈(0,π)得0<2 A <2π,0<2 B <2π,得2 A =2 B 或2 A +2 B =π,即 A = B 或 A + B =   . ∴△ ABC 为等腰三角形或直角三角形,故选D. 解法二:(同解法一)可得2 a 2 cos A sin B =2 b 2 cos B sin A . 由正、余弦定理,可得 a 2 ·   · b = b 2 ·   · a . ∴ a 2 ( b 2 + c 2 - a 2 )= b 2 ( a 2 + c 2 - b 2 ),即( a 2 - b 2 )( a 2 + b 2 - c 2 )=0.∴ a = b 或 a 2 + b 2 = c 2 , ∴△ ABC 为等腰三角形或直角三角形.故选D. 答案     D 方法总结 　要判断三角形的形状,应围绕三角形的边角关系进行思考,主要 看其是不是正三角形、等腰三角形、直角三角形、钝角三角形、等腰直 角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形 或直角三角形”的区别.依据已知条件中的边角关系判断时,主要有以下两 条途径: (1)通过正弦定理、余弦定理化边为角,利用三角恒等变换得出三角形内角 之间的关系进行判断; (2)利用正弦定理、余弦定理化角为边,通过代数恒等变换,求出三条边之 间的关系进行判断. 考法三 　与三角形的面积、范围有关的问题 例3　 (1)已知△ ABC 的三个内角 A , B , C 所对的边分别为 a , b , c ,若 b =1, c =   ,且 2sin( B + C )cos C =1-2cos A sin C ,则△ ABC 的面积是   (　　) A.   　    B.   　    C.   或   　    D.   或   (2)(2018吉林长春一模,15)在△ ABC 中,三个内角 A , B , C 的对边分别为 a , b , c , 若   cos A =sin A cos C ,且 a =2   ,则△ ABC 面积的最大值为 　　         . 解析　 (1)因为2sin( B + C )cos C =1-2cos A sin C ,所以2sin A cos C =1-2cos A sin C ,所以2sin A cos C +2cos A sin C =1,所以2sin( A + C )=1,所以2sin B =1,所以sin B =   . 因为 b < c ,所以 B < C ,所以角 B 为锐角, 所以cos B =   =   ,所以由余弦定理 b 2 = a 2 + c 2 -2 ac cos B ,可得1= a 2 +3-2 × a ×   ×   , 整理可得 a 2 -3 a +2=0,解得 a =1或 a =2. 故当 a =1时,△ ABC 的面积 S =   ac sin B =   × 1 ×   ×   =   ; 当 a =2时,△ ABC 的面积 S =   ac sin B =   × 2 ×   ×   =   .故选C. (2)因为   cos A =sin A cos C , 所以   b cos A -sin C cos A =sin A cos C , 所以   b cos A =sin( A + C ), 所以   b cos A =sin B , 所以   =   , 又   =   , a =2   , 所以   =   ,得tan A =   ,则 A =   , 由余弦定理得(2   ) 2 = b 2 + c 2 -2 bc ·   = b 2 + c 2 - bc , 由基本不等式得 bc ≤ 12,当且仅当 b = c =2   时等号成立. 从而△ ABC 面积的最大值为   × 12 ×   =3   . 答案　 (1)C　(2)3   方法总结 　1.与三角形面积有关的问题主要有两种:一是求三角形面积;二 是给出三角形的面积,求其他量.解题时主要应用三角形面积公式 S =   ab sin C =   ac sin B =   bc sin A ,此公式既与边长的乘积有关,又与角的三角函数值 有关,由此可以与正弦定理、余弦定理综合起来求解. 2.解与三角形中边角有关的量的取值范围时,主要是利用已知条件和有关 定理,将所求的量用三角形的某个内角或某条边表示出来,结合三角形边角 取值范围等求解即可. 考法四 　解三角形的实际应用 例4 　如图所示,某公路 AB 一侧有一块空地△ OAB ,其中 OA =3 km, OB =3   km,∠ AOB =90 ° ,当地政府拟在中间开挖一个人工湖△ OMN ,其中 M , N 都在 边 AB 上( M , N 不与 A , B 重合, M 在 A , N 之间),且∠ MON =30 ° . (1)若 M 在距离 A 点2 km处,求点 M , N 之间的距离; (2)为节省投入资金,人工湖△ OMN 的面积要尽可能小,试确定 M 的位置,使 △ OMN 的面积最小,并求出最小面积. 解题导引 　(1)由已知求出∠ OAB =60 ° .在△ OAM 中求得 OM =   .在△ OAN 中,sin∠ ONA =sin(∠ A +∠ AON ),在△ OMN 中,由正弦定理求出 MN . (2)在△ OAM ,△ OAN 中,用正弦定理求得 OM 及 ON , S △ OMN =   OM · ON ·sin∠ MON ,化简 S △ OMN 的表达式,由 θ <   求得 S △ OMN 的最小值. 解析　 (1)在△ OAB 中,因为 OA =3, OB =3   ,∠ AOB =90 ° ,所以∠ OAB =60 ° . 在△ OAM 中,由已知及余弦定理得 OM 2 = AO 2 + AM 2 -2 AO · AM ·cos A =7, 所以 OM =   ,所以cos∠ AOM =   =   , 在△ OAN 中,sin∠ ONA =sin(∠ A +∠ AON )=sin(∠ AOM +90 ° )=cos∠ AOM =   . 在△ OMN 中,由   =   得 MN =   ×   =   . 故点 M , N 之间的距离为   km. (2)设∠ AOM = θ ,0< θ <   . 在△ OAM 中,由   =   得 OM =   . 在△ OAN 中,由   =   得 ON =   =   .所以 S △ OMN =   OM · ON ·sin∠ MON =   ·   ·   ·   =   =   =   =   , 因为0< θ <   ,所以2 θ +   ∈   , 所以当2 θ +   =   ,即 θ =   时, S △ OMN 取最小值   . 所以应设计∠ AOM =   ,可使△ OMN 的面积最小,最小面积是   km 2 . 方法总结     解三角形应用题的方法 (1)解三角形应用题的一般步骤:   (2)解三角形应用题的两种情形: ①实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用 正弦定理或余弦定理求解. ②实际问题经抽象概括后,已知量与未知量涉及两个(或两个以上)三角形, 这时需作出这些三角形,先解够条件的三角形,然后逐步求出其他三角形中 的解,有时需设出未知量,从几个三角形中列出方程,解方程得出所要求的 解. (3)解三角形应用题应注意的问题: ①画出示意图后要注意寻找一些特殊三角形,如等边三角形、直角三角形 等,这样可以优化解题过程. ②解三角形时,为避免误差的累积,应尽可能用已知的数据(原始数据),少用 间接求出的量. 例 　如图,现要在一块半径为1 m,圆心角为   的扇形白铁片 AOB 上剪出一 个平行四边形 MNPQ ,使点 P 在弧 AB 上,点 Q 在 OA 上,点 M , N 在 OB 上,设∠ BOP = θ ,平行四边形 MNPQ 的面积为 S . (1)求 S 关于 θ 的函数关系式; (2)求 S 的最大值及相应的 θ 角. 实践探究 解题导引 　(1)虽然 P 点变化但 OP 不变,通过构造   与角 θ 所在的直角三角 形,将平行四边形的底和高用角 θ 表示,从而求出 S 关于 θ 的函数关系式.(2)利 用三角恒等变换先化简,再求 S 的最大值及相应的 θ 角. 解析 　(1)分别过 P , Q 作 PD ⊥ OB 于点 D , QE ⊥ OB 于点 E ,则四边形 QEDP 为 矩形. 由扇形半径为1 m,得 PD =sin θ , OD =cos θ . 在Rt△ OEQ 中, OE =   QE =   PD . MN = QP = DE = OD - OE =cos θ -   sin θ , 则 S = MN · PD =   ·sin θ =sin θ cos θ -   sin 2 θ , θ ∈   . (2)由(1)得 S =   sin 2 θ -   (1-cos 2 θ ) =   sin 2 θ +   cos 2 θ -   =   sin   -   , 因为 θ ∈   , 所以2 θ +   ∈   ,sin   ∈   . 当 θ =   时, S max =   m 2 . 规律方法 　(1)结合具体图形引进角为参数,利用三角函数的有关公式进行 化简,解决问题. (2)解决三角函数应用问题和解决一般应用性问题一样,先建模,再讨论变 量的范围,最后作出结论并回答问题. 题目价值 　本题以生活问题为背景,考查三角函数的实际应用.考查数学建 模的核心素养,以及学生处理信息的思维能力.