- 2021-06-23 发布 |
- 37.5 KB |
- 12页


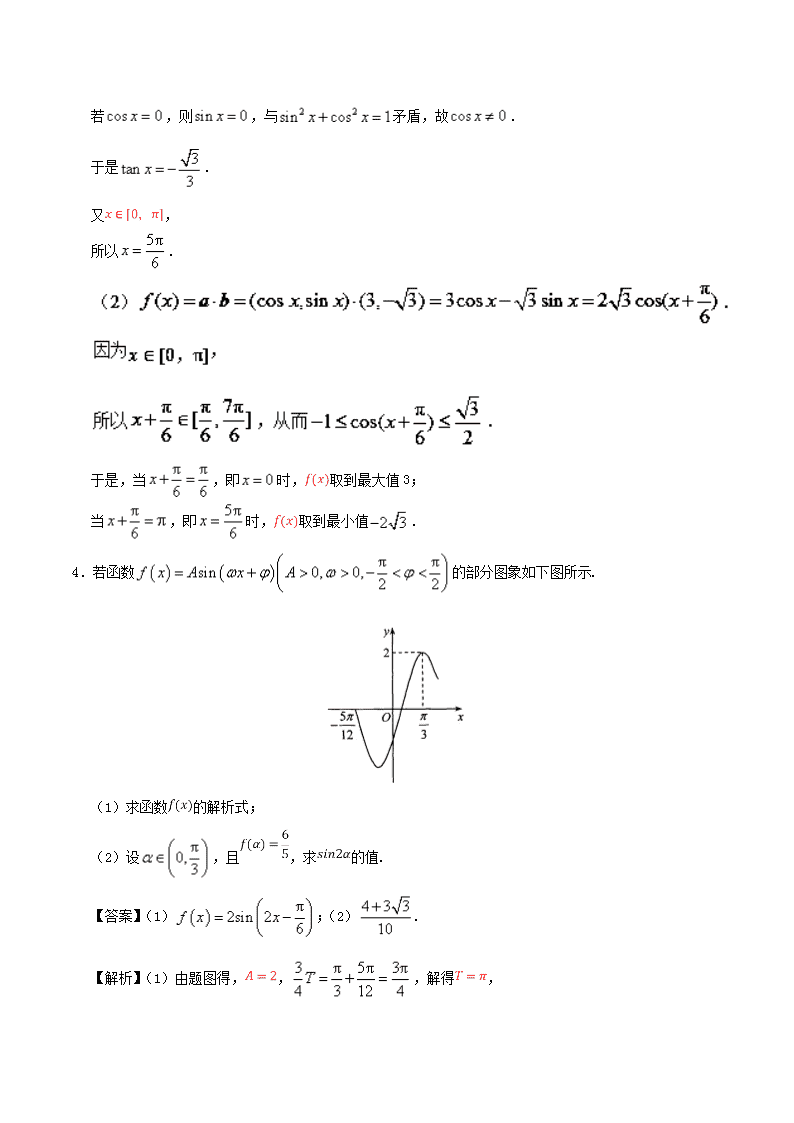
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题01 三角函数与解三角形(直通高考)-备战2018年高考之数学(文)解答题高分宝典
专题 01 三角函数与解三角形 1.(2017·浙江卷)已知函数 2 2sin cos 2 3sin cos ( )( ) x x xf x x x R . (1)求 2( )3f 的值. (2)求 ( )f x 的最小正周期及单调递增区间. 【答案】(1)2;(2)最小正周期为 ,单调递增区间为 2[ , ],6 3k k k Z . (2)由 2 2cos2 cos sinx x x 与sin 2 2sin cosx x x 得 ( ) cos2 3sin 2f x x x 2sin(2 )6x . 所以 ( )f x 的最小正周期是 . 由正弦函数的性质得 32 2 2 ,2 6 2k x k k Z , 解得 2 ,6 3k x k k Z , 所以, ( )f x 的单调递增区间是 2[ , ],6 3k k k Z . 【名师点睛】本题主要考查了三角函数的化简,以及函数 xAy sin 的性质,是高考中的常考知 识点,属于基础题,强调基础的重要性;三角函数解答题中,涉及到周期,单调性,单调区间以及最值 等考点时,都属于考查三角函数的性质,首先应把它化为三角函数的基本形式即 xAy sin ,然 后利用三角函数 uAy sin 的性质求解. 2.(2017·天津卷文)在 ABC△ 中,内角 , ,A B C 所对的边分别为 , ,a b c .已知 sin 4 sina A b B , 2 2 25( )ac a b c . (1)求 cos A的值; (2)求sin(2 )B A 的值. 【答案】(1) 5 5 ;(2) 2 5 5 . (2)由(1)可得 2 5sin 5A ,代入 sin 4 sina A b B ,得 sin 5sin 4 5 a AB b . 由(1)知 A 为钝角, 所以 2 2 5cos 1 sin 5B B . 于是 4sin 2 2sin cos 5B B B , 2 3cos2 1 2sin 5B B , 故 4 5 3 2 5 2 5sin(2 ) sin 2 cos cos2 sin ( )5 5 5 5 5B A B A B A . 【名师点睛】(1)利用正弦定理进行“边转角”可寻求角的关系,利用“角转边”可寻求边的关系,利 用余弦定理借助三边关系可求角,利用两角和差的三角公式及二倍角公式可求三角函数值. (2)利用正、余弦定理解三角形是高考的高频考点,常与三角形内角和定理、三角形面积公式等相结合, 利用正、余弦定理进行解题. 3.(2017·江苏卷)已知向量 (cos , sin ), (3, 3), [0,π].x x x a b (1)若 a∥b,求 x 的值; (2)记 ( )f x a b ,求 ( )f x 的最大值和最小值以及对应的 x 的值. 【答案】(1) 5π 6x ;(2) 0x 时, 取得最大值 3; 5π 6x 时, 取得最小值 2 3 . 【解析】(1)因为 co( )s ,sinx xa , (3, 3) b ,a∥b, 所以 3cos 3sinx x . 若 cos 0x ,则sin 0x ,与 2 2sin cos 1x x 矛盾,故 cos 0x . 于是 3tan 3x . 又 , 所以 5π 6x . 于是,当 π π 6 6x ,即 0x 时, 取到最大值 3; 当 π 6x ,即 5π 6x 时, 取到最小值 2 3 . 4.若函数 π πsin 0, 0, 2 2f x A x A 的部分图象如下图所示. (1)求函数 的解析式; (2)设 π0, 3 ,且 ,求 的值. 【答案】(1) π2sin 2 6f x x ;(2) 4 3 3 10 . 【解析】(1)由题图得, , 3 π 5π 3π 4 3 12 4T ,解得 , 于是由 2π πT ,得 . ∵ π 2π2sin 23 3f ,即 2πsin 13 , ∴ 2π π2 π3 2k k Z, ,即 π2 π 6k k Z, , 又 π π 2 2 , , ∴ π 6 , ∴ π2sin 2 6f x x . ∴ π π π2 6 6 2 , , ∴ 2π π 4cos 2 1 sin 26 6 5 . ∴ π πsin 2 sin 2 6 6 π π π πsin 2 cos cos 2 sin6 6 6 6 3 3 4 1 5 2 5 2 4 3 3 10 . 5.已知向量 1,sinxa , cos , 3xb . (1)若 a b ,求 tan2x 的值; (2)令 f x a b ,把函数 f x 的图象上每一点的横坐标都缩小为原来的一半(纵坐标不变),再把 所得图象沿 x 轴向左平移 π 12 个单位,得到函数 y g x 的图象,求函数 y g x 的单调递增区间. 【答案】(1) 3 ;(2) 5π ππ , π12 12k k k Z . 【解析】(1) a b , 1,sin cos , 3 cos 3sin 0x x x x a b , 1tan 3 x , 2 2tantan 2 31 tan xx x . (2) π1,sin cos , 3 cos 3 sin 2sin 6x x x x x a b , π2sin 6f x x , 由 π π π2 π 2 2 π2 3 2k x k k Z 得 5π ππ π12 12k x k k Z , g x 的单调递增区间是 5π ππ , π12 12k k k Z . 6.已知 ABC△ 的三个内角 , ,A B C 对应的边分别为 , ,a b c ,且 2cos cos cosB c A a C b . (1)证明: , ,A B C 成等差数列; (2)若 ABC△ 的面积为 3 3 2 ,求b 的最小值. 【答案】(1)见解析;(2) 6 . 【解析】(1)因为 2cos cos cosB c A a C b , 所以由正弦定理得 2cos sin cos sin cos sinB C A A C B ,即 2cos sin sinB A C B . 在 ABC△ 中, sin sinA C B 且sin 0B , 所以 1cos 2B . 因为 0,πB , 所以 π 3B . 又因为 πA B C , 所以 2π 23A C B . 所以 , ,A B C 成等差数列. (2)因为 1 3 3sin2 2ABCS ac B △ , 所以 6ac . 所以 2 2 2 2 22 cos 6b a c ac B a c ac ac ,当且仅当 a c 时取等号. 所以b 的最小值为 6 . 7.如图,在 ABC△ 中, π , 23B BC ,点 D 在边 AB 上, ,AD DC DE AC , E 为垂足. (1)若 BCD△ 的面积为 3 3 ,求 AB 的长; (2)若 6 2ED ,求角 A 的大小. 【答案】(1) 2 7 2 3 ;(2) π 4 . 【解析】(1)∵ BCD△ 的面积为 3 3 , π , 23B BC , ∴ 1 π 32 sin2 3 3BD , ∴ 2 3BD . 在 BCD△ 中,由余弦定理可得 2 2 4 2 1 2 72 cos 4 2 29 3 2 3CD BC BD BC BD B . ∴ 2 7 2 2 7 2 3 3 3AB AD BD CD BD . ∵ 2BDC A , ∴ 2 6 sin2 2sin sin60A A , ∴ 2cos 2A . ∴ π 4A . 【名师点睛】此题主要考查了正弦定理、余弦定理、以及三角恒等变换中倍角公式在解三角形中的应用, 属于中档题型,也是常考考点.在解决此类问题的过程中,常将所求角、边与已知的角、边转化集中到同 一个三角形,再运用三角公式进行恒等变形及运算,以已知角为线索,寻找合适的正弦定理、余弦定理, 从而解决问题. 8.已知函数 π π π( ) cos(2 ) 2sin( )cos( )( )3 4 4f x x x x x R . (1)求函数 ( )f x 的最小正周期及 ( )f x 在区间 π 2π[ , ]12 3 上的值域; (2)在 ABC△ 中, 5AB , 7BC .若 1( ) 2f A ,求 ABC△ 的面积. 【答案】(1) πT ,值域是 1[ ,1]2 ;(2) 5 3 2 或15 3 4 . 3 1sin 2 cos22 2x x πsin(2 )6x . )(xf 的最小正周期为 2π π2T ; ∵ π 2π[ , ]12 3x , ∴ π 7π2 [0, ]6 6x , ∴ max π π π π( ) ( ) sin(2 ) sin 13 3 6 2f x f , min 2π 2π π 7π 1( ) ( ) sin(2 ) sin3 3 6 6 2f x f , ∴ ( )f x 在区间 π 2π[ , ]12 3 上的值域是 1[ ,1]2 . (2)由 1( ) 2f A 得 π 1sin(2 )6 2A ,即 π 6A , 由余弦定理得 27 25 5 3 ( 2 3)( 3 3) 0b b b b , ∴ 2 3b 或 3 3b , ∴ ABC△ 的面积为 1 1 5 35 2 32 2 2ABCS 或 1 1 15 35 3 32 2 4ABCS . 9.已知函数 5( ) sin( 2 ) 2sin( )cos( )6 4 4f x x x x . (1)求函数 ( )f x 的最小正周期和单调递增区间; (2)若 [ , ]12 3x ,且 ( ) 4 ( ) cos(4 )3F x f x x 的最小值是 3 2 ,求实数 的值. 【答案】(1) πT ,单调递增区间为[ , ],6 3k k k Z ;(2) 1 2 . 1 3cos2 sin 2 cos22 2x x x sin(2 )6x . ∴ 2 2T , 由 2 2 2 ,2 6 2k x k k Z ,得 ,6 3k x k k Z , ∴函数 ( )f x 的单调递增区间为[ , ],6 3k k k Z . (2) ( ) 4 ( ) cos(4 )3F x f x x 24 sin(2 ) [1 2sin (2 )]6 6x x 22sin (2 ) 4 sin(2 ) 16 6x x 2 22[sin(2 ) ] 1 26x , ∵ [ , ]12 3x , ∴ 0 2 6 2x , ∴ 0 sin(2 ) 16x . ①当 0 时,当且仅当sin(2 ) 06x 时, ( )f x 取得最小值 1 ,这与已知不相符; ②当 0 1 时,当且仅当sin(2 )6x 时, ( )f x 取得最小值 21 2 ,由已知得 2 31 2 2 , 解得 1 2 ; 综上所述, 1 2 . 【名师点睛】本题主要考查三角函数的图象与性质,二倍角公式,两角和与差的正、余弦公式,考查了 转化思想与分类讨论思想、逻辑推理能力与计算能力. (1)求解关于三角函数的图象与性质的问题时,一定要将函数解析式化简为 ( ) sin( )f x A x ( ( ) cos( )f x A x )的形式,再根据正弦(余弦)函数的性质求解即可; (2)化简可得 ( ) 2[sin(2 )6F x x 2 2] 1 2 ,可以利用换元法将此式变形为 22( ) 1y t 22 , πsin(2 ) [0,1]6t x ,然后利用对称轴t 与定义域[0,1] 之间的关系进行 讨论,即分 0 、 1 、 0 1 三种情况讨论求解即可. 10.在海岛 A 上有一座海拔1km 的山峰,山顶设有一个观察站 P ,有一艘轮船按一固定方向作匀速直线航 行,上午11:00 时,测得此船在岛北偏东15 、俯角为30 的 B 处,到11:10时,又测得该船在岛北偏 西 45 、俯角为 60 的C 处. (1)求船的航行速度; (2)求船从 B 到C 行驶过程中与观察站 P 的最短距离. 【答案】(1) 2 21 km/h ;(2) 259 km14 . 在 ACB△ 中, 15 45 60CAB , 由余弦定理得 2 2 3 3 213 2 3 cos603 3 3BC , 216 2 21 km/h,3x ∴船的航行速度为 2 21 km/h . (2)作 AD BC 于点 ,D 当船行驶到点 D 时, AD 最小,从而 PD 最小, 此时, 3 33sin60 33 2 71421 3 AB ACAD BC , 23 2591 714 14PD , 船在行驶过程中与观察站 P 的最短距离为 259 km14 .查看更多