2020高中数学 第二章 函数§2.3函数的单调性

2020高中数学 第二章 函数§2.3函数的单调性

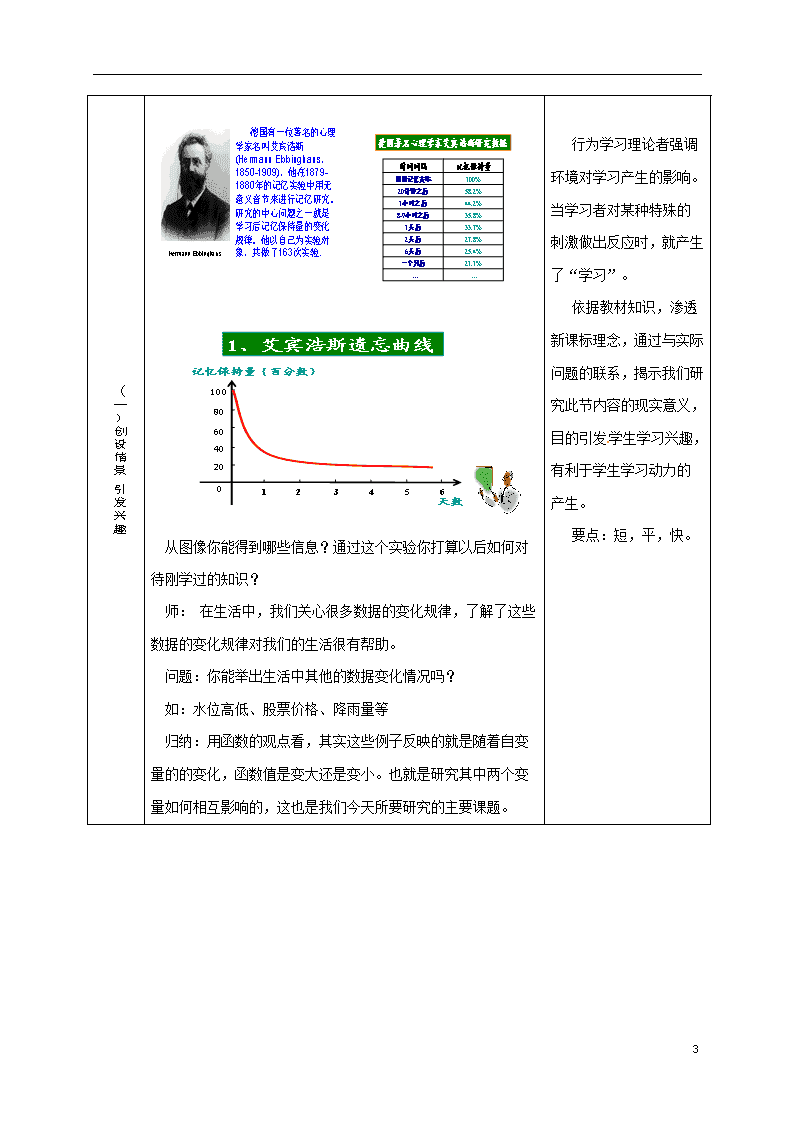
‎§2.3函数的单调性 一、教材分析-----教学内容、地位和作用 本课是北师大版新课标普通高中数学必修一第二章第3节《函数的单调性》的内容，函数的单调性是函数众多性质中的重要性质之一，函数的单调性一节中的知识是今后研究具体函数的单调性理论基础；在解决函数值域、定义域、不等式、比较两数大小等具体问题中均有着广泛的应用；在历年的高考中对函数的单调性考查每年都有涉及；同时在这一节中利用函数图象来研究函数性质的数形结合思想将贯穿于我们整个高中数学教学。‎ 在学生现有认知结构中能根据函数的图象观察出“随着自变量的增大函数值增大”等变化趋势，所以在教学中要充分利用好函数图象的直观性、发挥好多媒体教学的优势；‎ 在本节课是以函数的单调性的概念为主线，它始终贯穿于整个课堂教学过程；这是本节课的重点内容。‎ 利用函数的单调性的定义证明具体函数的单调性一个难点，也是对函数单调性概念的深层理解，且在“作差、变形、定号”过程学生不易掌握。‎ 学生刚刚接触这种证明方法，给出一定的步骤是必要的，有利于学生理解概念，也可以对学生掌握证明方法、形成证明思路有所帮助。另外，这也是以后要学习的不等式证明的比较法的基本思路，现在提出来对今后的教学也有了一定的铺垫。‎ 二、教学目标：‎ 根据新课标的要求，以及对教材结构与内容分析，考虑到学生已有的认知结构及心理特征 ，制定如下教学目标：‎ ‎ (一)三维目标 ‎1 知识与技能：‎ （1） 使学生理解函数单调性的概念， 能判断并证明一些简单函数在给定区间上的单调性。‎ （2） 通过函数单调性的教学，逐步培养学生观察、分析、概括与合作能力；‎ ‎ 2 过程与方法： ‎ （1） 通过本节课的学习，通过“数与形”之间的转换，渗透数形结合的数学思想。‎ （2） 通过探究活动，明白考虑问题要细致、缜密，说理要严密、明确。‎ ‎3 情感，态度与价值观：在平等的教学氛围中，通过学生之间、师生之间的交流、合作与评价，拉近学生之间、师生之间的情感距离，培养学生对数学的兴趣。。‎ 10‎ ‎（二）重点、难点 重点：函数单调性的概念: ‎ 为了突出重点，使学生理解该概念，整个过程分为：‎ 作图象并观察图象→讨论：函数图象的变化趋势是什么？→‎ 在这种变化趋势下， x与函数值y是如何相互影响的？→你能从量的角度出一个缜密的，完善的定义来吗？‎ 每个步骤都是在教师的参与下与引导下，通过学生与学生之间，师生之间的合作交流，不断反省，探索，直到完善结论，最终达到一个严密，简洁的定义。‎ 难点：函数单调性的判断与推证：‎ 突破该难点的：通过对照、分析定义，引导学生，概括出证明方法及步骤：“取量定大小，作差定符号，判断得结论”，并注意解题过程的规范性与严谨性。‎ 四、教学方法：‎ 合作学习认为教学是师生之间、生生之间相互作用的过程，强调多边互动，共同掌握知识。视教学为师生平等参与和互动的过程，强调教师只是小组中的普通一员，起到一个引导者，管理者角色。在课堂教学中要加强知识发生过程的教学，充分调动学生的参与的积极性，有效地渗透数学思想方法，发展学生个性品质，从而达到提高学生整体的数学素养的目的。‎ 结合教学目标和学生情况我采用合作交流，探究学习相结合的教学方法。‎ 五 .教学手段 多媒体 六、教学过程 教学环节 教学过程 设计意图 10‎ ‎（一）创设情景，引发兴趣 ‎ 从图像你能得到哪些信息？通过这个实验你打算以后如何对待刚学过的知识？‎ 师： 在生活中，我们关心很多数据的变化规律，了解了这些数据的变化规律对我们的生活很有帮助。‎ 问题：你能举出生活中其他的数据变化情况吗？‎ 如：水位高低、股票价格、降雨量等 归纳：用函数的观点看，其实这些例子反映的就是随着自变量的的变化，函数值是变大还是变小。也就是研究其中两个变量如何相互影响的，这也是我们今天所要研究的主要课题。‎ 行为学习理论者强调环境对学习产生的影响。当学习者对某种特殊的刺激做出反应时，就产生了“学习”。‎ 依据教材知识，渗透新课标理念，通过与实际问题的联系，揭示我们研究此节内容的现实意义，目的引发学生学习兴趣，有利于学生学习动力的产生。‎ 要点：短，平，快。‎ 10‎ ‎︵‎ 二︶合作交流，建构数学 多媒体展示在上节课所做的几个函数图象，并据此讨论下列问题，‎ 问题1、说一说所画函数的图象的变化趋势。‎ 观察得到：随着x值的增大，函数的函数图象有的呈逐渐上升的趋势，有的呈下降的趋势，有的在一个区间内呈上升趋势，在另一个区间内呈逐渐下降的趋势。‎ ‎(注意一定要提醒：是从左到右的看)‎ 问题2：你能明确的说出“图象呈逐渐上升趋势”的意思吗？‎ 讨论得到：‎ 在某一个区间内，当x值增大时，函数值y也增大图象在该区间内呈上升趋势。‎ 在某一个区间内，当x值增大时，函数值y也反而减小图象在该区间内呈下降趋势。‎ 在众多的函数中，很多函数都具有这种性质，因此我们有必要对函数的这种性质做进一步的讨论与研究。这就是我们今天这一节课的主题。‎ 函数的这种性质，我们就称为函数的单调性。‎ ‎(对每一个问题，小组成员先独立做，再分别说出自己的想法，然后讨论，形成集体的意见。)‎ ‎1、通过一系列的问题，引发对概念的全面思考。从具体到抽象，再从抽象到具体，并通过合作交流，增强学生对概念的理解，不断的修正、完善结论，达到建构数学的目的。‎ ‎2、教学实践证明，小组内成员合作，组间成员竞争的讨论是一种有效的教学策略，使得整个评价的重心同个人之间竞争转为团体合作达标。并能使教师与学生、学生与学生之间有更多的交往、互动的机会。‎ 10‎ ‎︵‎ 二︶合作交流，建构数学 问题3：如何用数学语言表述一个函数是在整个定义域内是增加的呢？‎ 我们刚才已经对函数的单调性，做了定性的分析，我们如何从量的角度来刻画这种性质。你能给出一个确切的定义来吗？请用你自己的话表达出来，并说给你的小组成员听，并与他交流后，形成集体意见，再展示给大家。‎ 教师巡视，视小组讨论情况，可提示：‎ ‎（1）对于某函数，若在其定义域上，当x＝1时， y＝1；当 x＝2时，y＝3 ，能否说在其定义域上 y 随 x 的增大而增大呢? ‎ ‎（2）若x＝1，2，3，4，时，相应地 y＝1，3，4，6，能否说在其定义域上，y 随x 的增大而增大呢？‎ ‎（3）若有n个正数x1< x2f(),则说f(x) 在定义域内是减少的（递减的），即称这个函数为减函数。‎ 它也是引导学生积极参与教学过程的重要措施，是培养学生合作精神和激发学生创新意识的重要手段，也是促使每个学生得到充分发展的有效途径 ‎3、重点：学生能否抓住定义中的关键词“给定区间”、“任意”和“都有”，是能否正确，深入透彻地理解和掌握概念的重要一环。‎ 分析定义，使学生把定义与图形结合起来，使新旧知识 融为一体，加深对概念的理解，渗透数形结合的分析问题的数学思想方法。‎ 10‎ 增函数的本质是在整个定义域上，较大的自变量对应较大的函数值，减函数反之。‎ 单调区间 ；如果函数y=f(x)在定义域内某个区间I上是增加的或是减少的,那么就说函数y=f(x)在区间I上具有单调性.‎ ‎ 单调增区间和单调减区间统称为单调区间.‎ 10‎ ‎︵‎ 三︶数学运用，巩固新知 让学生进一步理解一般函数单调区间的定义，‎ ‎(1)区间的端点要不要？‎ ‎(2)在这里一定要强调单调性只是函数的“局部性质”它与区间密不可分。-----不能把函数的单调区间写成 ‎ ‎ ‎ 10‎ ‎︵‎ 三︶数学运用，巩固新知 ‎2、由于例2难度较大，学生难以从中归纳出 证明方法及步骤，因而有必要先详细讲解，通过分析、引导学生抽象、概括出方法及步骤，提示学生注意证明过程的规范性及严谨性。‎ ‎ 归纳证明方法并加以比较说明；使学生突破本节的难点，掌握重点内容。‎ 基本步骤：‎ ‎“取量定大小，作差定符号，判断定结论”其中第二环节是难点“作差→变形→判断正负”。‎ 10‎ ‎︵‎ 三︶数学运用，巩固新知 练习的设定也是由浅入深层层推进的。‎ 10‎ ‎(四)回顾总结，加深理解 ‎ 请同学小结一下这节课的主要内容，有哪些是词语特别注意的？(请一个思路清晰，善于表达的学生口述，教师可从中给予提示)‎ ‎1、函数单调性的定义，注意定义中的关键词。‎ ‎2、证明函数单调性的一般步骤；‎ ‎3、在写单调区间时，不要轻易用并集的符号连接；‎ 课后知识性内容总结，把课堂内容转化为学生的素质 ‎( 五)兼顾差异，分层练习 必做：习题2.3：A组第2、3、4题 选做：研究 的单调性，并给出严格证明，你能求出该函数的值域吗？ ‎ ‎1、针对学生个体的差异设置分层练习。既注重课内基础知识掌握，又兼顾了有余力的学生的能力的提高。 ‎ ‎2、提出新的课题是想把问题研究引向课外，激发学生兴趣，为以后学习“最值”作好充分的准备。‎ 特别说明：‎ 增函数和减函数的概念新旧教材有所不同，本教案以新教材为准。‎ 旧教材：如果对于属于定义域内某个区间上的任意两个自变量的值，，当<时，都有f()f(),那么就说f(x)在这个区间上是减函数。‎ 新教材：如果函数y=f(x)在整个定义域内是增加的或是减少的，我们分别称这个函数为增函数或减函数。‎ 10‎