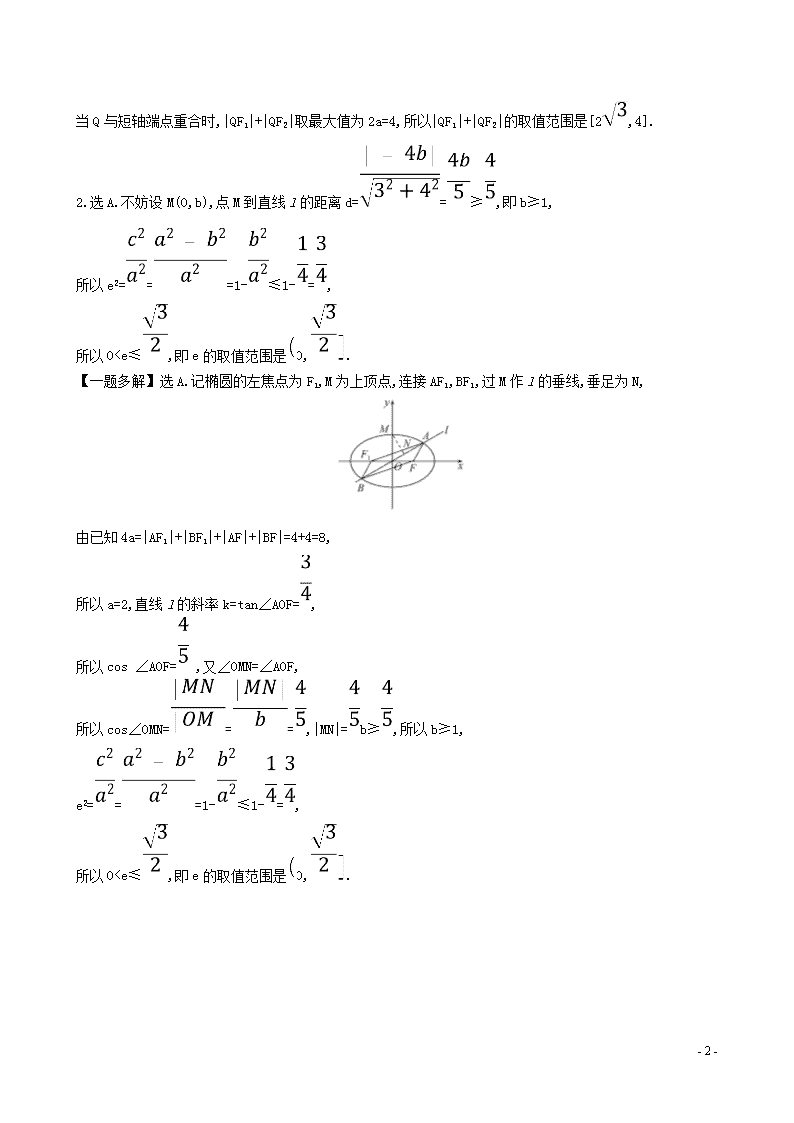高考数学一轮复习第十章平面解析几何10-9-3圆锥曲线的范围问题练习理北师大版

高考数学一轮复习第十章平面解析几何10-9-3圆锥曲线的范围问题练习理北师大版

‎10.9.3 圆锥曲线的范围问题 核心考点·精准研析 考点一　几何法求范围 ‎ ‎1.已知直线l1:mx-y+m=0与直线l2:x+my-1=0的交点为Q,椭圆+y2=1的焦点为F1,F2,则|QF1|+|QF2|的取值范围是 (　　)‎ A.[2,+∞) B.[2,+∞)‎ C.[2,4] D.[2,4]‎ ‎2.已知椭圆E:+=1(a>b>0)的右焦点为 F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于 A,B两点.若|AF|+|BF|=4,点M到直线l的距离不小于,则椭圆E的离心率的取值范围是 (　　) ‎ ‎ A. 0, B.0, C. ,1 D.,1‎ ‎3.过双曲线-=1(a>0,b>0)的右顶点且斜率为2的直线,与该双曲线的右支交于两点,则此双曲线离心率的取值范围为________________. ‎ ‎【解析】1.选D.椭圆+y2=1的焦点为:F1(-,0),‎ F2(,0),由l1与l2方程可知l1⊥l2,‎ 直线l1:mx-y+m=0与直线l2:x+my-1=0的交点为Q,且两条直线分别经过定点(-1,0),(1,0),‎ 所以它们的交点Q满足:x2+y2=1(x≠-1),‎ 当Q与(1,0)重合时,|QF1|+|QF2|取最小值为 ‎|F1F2|=2,‎ - 15 -‎ 当Q与短轴端点重合时,|QF1|+|QF2|取最大值为2a=4,所以|QF1|+|QF2|的取值范围是[2,4].‎ ‎2.选A.不妨设M(0,b),点M到直线l的距离d==≥,即b≥1,‎ 所以e2===1-≤1-=,‎ 所以00,b>0)的右顶点且斜率为2的直线,与该双曲线的右支交于两点,可得<2.所以e==<=,因为e>1,所以1b>0),左右焦点分别为F1,F2,R为短轴的一个端点,且△RF1F2的面积为.设过原点的直线l与椭圆C交于A,B两点,P为椭圆C上异于A,B的一点,且直线PA,PB的斜率都存在,kPAkPB=-.‎ ‎(1)求a,b的值.‎ ‎(2)设Q为椭圆C上位于x轴上方的一点,且QF1⊥x轴,M,N为椭圆C上不同于Q的两点,且∠MQF1=∠NQF1,设直线MN与y轴交于点D(0,d),求d的取值范围.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)‎ 求参数a,b 点差法转化kPAkPB=-,结合△RF1F2的面积列出方程组求解 ‎(2)‎ ‎①设直线QM的方程 将两角相等转化为两直线QM,QN斜率之间的关系 ‎②求直线MN的斜率 将直线方程与椭圆方程联立,分别求出M、N点的横坐标,利用两点坐标表示出直线MN的斜率.‎ ‎③求d所满足的不等式 将直线MN的方程与椭圆方程联立,由位置关系列出不等关系 ‎④解不等式求范围 解所得不等式即可求得d的取值范围 ‎【解析】(1)设A(x1,y1),P(x2,y2),则B(-x1,-y1),‎ 进一步得,+=1,+=1,‎ 两个等式相减得,+=0,‎ 所以·=-,‎ - 15 -‎ 所以kPA·kPB=-,因为kPA·kPB=-,所以-=-,即=,设b=t,a=2t(t>0),‎ 因为a2=b2+c2,所以c=t,‎ 由△RF1F2的面积为得,=,即bc=,即t2=,t=1,‎ 所以a=2,b=.‎ ‎(2)设直线QM的斜率为k,‎ 因为∠MQF1=∠NQF1,所以QM,QN关于直线QF1对称,所以直线QN的斜率为-k,‎ 算得F1(-1,0),Q,‎ 所以直线QM的方程是y-=k(x+1),‎ 设M(x3,y3),N(x4,y4)‎ 由 消去y得,‎ ‎(3+4k2)x2+(12+8k)kx+(4k2+12k-3)=0,‎ 所以-1·x3=,所以x3=,‎ 将上式中的k换成-k得,x4=,‎ 所以kMN====-,‎ - 15 -‎ 所以直线MN的方程是y=-x+d,‎ 代入椭圆方程+=1得,x2-dx+d2-3=0,所以 Δ=(-d)2-4(d2-3)>0,所以-2-×(-1)+d,所以-2b>0)的上顶点和左焦点,若EF与圆x2+y2=相切于点T,且点T是线段EF靠近点E的三等分点.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)直线l:y=kx+m与椭圆C只有一个公共点P,且点P在第二象限,过坐标原点O且与l垂直的直线l′与圆x2+y2=8相交于A,B两点,求△PAB面积的取值范围.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)‎ 求参数a,b 根据已知分别求出a,b的值.‎ ‎(2)‎ ‎①建立k,m的关系式 直线方程与椭圆方程联立,利用方程只有一解即可建立两者的关系式 ‎②求P到直线l′的距离 求P点坐标,代入距离公式求解 ‎③表示△PAB面积 利用三角形面积公式建立目标函数 ‎④求取值范围 根据目标函数的结构特征,利用基本不等式求解最值,从而确定其取值范围 - 15 -‎ ‎【解析】(1) OT2=ET·TF=a·a=,‎ a2=6,b2=OE2=OT2+ET2=2,‎ 椭圆C的标准方程为+=1.‎ ‎(2)由得,‎ ‎(3k2+1)x2+6kmx+3m2-6=0,‎ 因为直线l:y=kx+m与椭圆C相切于点P, 所以Δ=(6km)2-4(3k2+1)(3m2-6)=12(6k2+2-m2)=0,即m2=6k2+2,解得x=,y=,‎ 即点P的坐标为,‎ 因为点P在第二象限,所以k>0,m>0,‎ 所以m=,所以点P的坐标为 ‎,设直线l′与l垂直交于点Q,‎ 则|PQ|是点P到直线l′的距离,‎ 设直线l′的方程为y=-x,‎ 则|PQ|===,‎ - 15 -‎ 所以S△PAB=×4×|PQ|=≤==4-4,‎ 当且仅当3k2=,即k2=时,取得最大值4-4,所以△PAB面积的取值范围为(0,4-4].‎ ‎1.已知椭圆C:+=1(a>b>0)的焦距为2,且C与y轴交于A(0,-1),B(0,1)两点.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)设P点是椭圆C上的一个动点且在y轴的右侧,直线PA,PB与直线x=3交于M,N两点.若以MN为直径的圆与x轴交于E,F两点,求P点横坐标的取值范围.‎ ‎【解析】(1)由题意可得,b=1,c=,所以a=2, 椭圆C的标准方程为+y2=1.‎ ‎(2)方法一:设P(x0,y0)(00,又00),与椭圆x2+4y2=4联立得:(1+4)x2-8k1x=0,xP=,同理设直线BP的方程为y=k2x+1,可得xP=,由=,可得4k1k2=-1,所以M(3,3k1-1),‎ N(3,3k2+1),MN的中点为,所以以MN为直径的圆为(x-3)2+=.‎ 当y=0时,(x-3)2+=,所以(x-3)2=,‎ 因为MN为直径的圆与x轴交于E,F两点,所以>0,‎ 代入4k1k2=-1得:<0,所以0,整理得m2<4k2+3.①设A(x1,y1),B(x2,y2),‎ 则x1+x2=-,x1x2=.‎ 设点E的坐标为(x0,y0),则x0=-,‎ 所以y0=kx0+m=-+m=,‎ - 15 -‎ 所以点E的坐标为.‎ 所以直线l2的斜率为k′==.‎ 又直线l1和直线l2垂直,则·k=-1,所以m=-.‎ 将m=-代入①式,可得<4k2+3.解得k>或k<-.‎ 所以直线l1的斜率的取值范围为∪.‎ ‎1.(2020·南昌模拟)已知椭圆C:+=1(a>b>0)的离心率为,短轴长为2.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)设直线l:y=kx+m与椭圆C交于M,N两点,O为坐标原点,若kOM·kON=,求原点O到直线l的距离的取值范围.‎ ‎【解析】(1)由题知e==,2b=2,‎ 又a2=b2+c2,所以b=1,a=2,‎ 所以椭圆C的标准方程为+y2=1.‎ - 15 -‎ ‎(2)设M(x1,y1),N(x2,y2),联立方程 得(4k2+1)x2+8kmx+4m2-4=0,‎ 依题意,Δ=(8km)2-4(4k2+1)(4m2-4)>0,‎ 化简得m2<4k2+1,①‎ x1+x2=-,x1x2=,‎ y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.‎ 若kOM·kON=,则=,即4y1y2=5x1x2,‎ 所以(4k2-5)x1x2+4km(x1+x2)+4m2=0,‎ 所以(4k2-5)·+4km·+4m2=0,‎ 即(4k2-5)(m2-1)-8k2m2+m2(4k2+1)=0,‎ 化简得m2+k2=②,由①②得0≤m2<,0,‎ 设Q,‎ 因为P在椭圆上,所以+=1,‎ 解得y0=,即P.‎ 因为F1,由PQ=λF1Q得,c-x1=λ,-y1=-λy1,‎ 解得x1=-c,y1=-,‎ 所以Q.‎ 因为点Q在椭圆上,所以e2+=1,‎ 即e2+=,所以(λ+2)e2=λ-2,从而e2=.‎ 因为4≤λ≤5,所以≤e2≤.解得≤e≤,‎ 所以椭圆C的离心率的取值范围为.‎ - 15 -‎ - 15 -‎