2012年江西省高考数学试卷（文科）

2012年江西省高考数学试卷（文科）

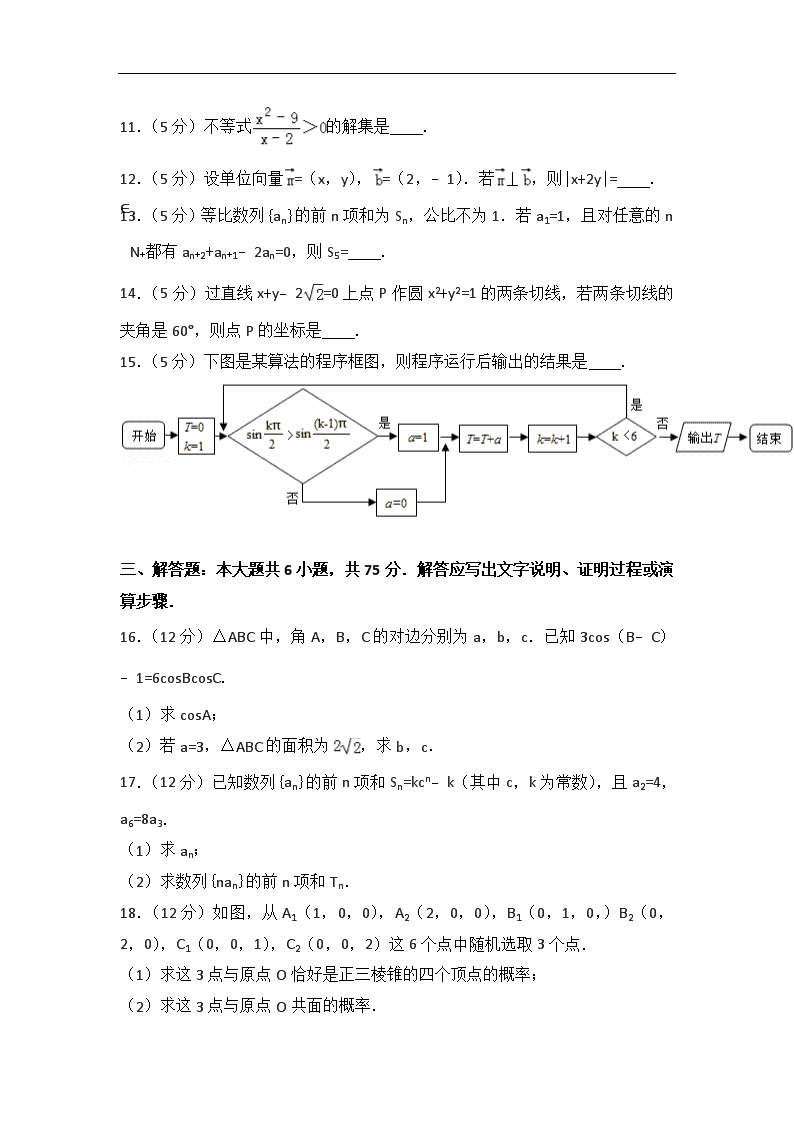
‎2012年江西省高考数学试卷（文科）‎ ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1．（5分）若复数z=1+i（i为虚数单位） 是z的共轭复数，则z2+2的虚部为（　　）‎ A．0 B．﹣1 C．1 D．﹣2‎ ‎2．（5分）若全集U={x∈R|x2≤4}，则集合A={x∈R||x+1|≤1}的补集∁UA为（　　）‎ A．{x∈R|0＜x＜2|} B．{x∈R|0≤x＜2|} C．{x∈R|0＜x≤2|} D．{x∈R|0≤x≤2|}‎ ‎3．（5分）设函数f（x）=，则f（f（3））=（　　）‎ A． B．3 C． D．‎ ‎4．（5分）若=，则tan2α=（　　）‎ A．﹣ B． C．﹣ D．‎ ‎5．（5分）观察下列事实|x|+|y|=1的不同整数解（x，y）的个数为4，|x|+|y|=2的不同整数解（x，y）的个数为8，|x|+|y|=3的不同整数解（x，y）的个数为12 …．则|x|+|y|=20的不同整数解（x，y）的个数为（　　）‎ A．76 B．80 C．86 D．92‎ ‎6．（5分）小波一星期的总开支分布图如图1所示，一星期的食品开支如图2所示，则小波一星期的鸡蛋开支占总开支的百分比为（　　）‎ A．30% B．10% C．3% D．不能确定 ‎7．（5分）若一个几何体的三视图如图所示，则此几何体的体积为（　　）‎ A． B．5 C． D．4‎ ‎8．（5分）椭圆（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F1，F2．若|AF1|，|F1F2|，|F1B|成等比数列，则此椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎9．（5分）已知f（x）=sin2（x+），若a=f（lg5），b=f（lg），则（　　）‎ A．a+b=0 B．a﹣b=0 C．a+b=1 D．a﹣b=1‎ ‎10．（5分）如图，|OA|=2（单位：m），OB=1（单位：m），OA与OB的夹角为，以A为圆心，AB为半径作圆弧与线段OA延长线交与点C．甲、乙两质点同时从点O出发，甲先以速度1（单位：m/s）沿线段OB行至点B，再以速度3（单位：m/s）沿圆弧行至点C后停止；乙以速率2（单位：m/s）沿线段OA行至A点后停止．设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）（S（0）=0），则函数y=S（t）的图象大致是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题：本大题共5小题，每小题5分，共25分．‎ ‎11．（5分）不等式的解集是　　．‎ ‎12．（5分）设单位向量=（x，y），=（2，﹣1）．若⊥，则|x+2y|=　　．‎ ‎13．（5分）等比数列{an}的前n项和为Sn，公比不为1．若a1=1，且对任意的n∈N+都有an+2+an+1﹣2an=0，则S5=　　．‎ ‎14．（5分）过直线x+y﹣2=0上点P作圆x2+y2=1的两条切线，若两条切线的夹角是60°，则点P的坐标是　　．‎ ‎15．（5分）下图是某算法的程序框图，则程序运行后输出的结果是　　．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎16．（12分）△ABC中，角A，B，C的对边分别为a，b，c．已知3cos（B﹣C）﹣1=6cosBcosC．‎ ‎（1）求cosA；‎ ‎（2）若a=3，△ABC的面积为，求b，c．‎ ‎17．（12分）已知数列{an}的前n项和Sn=kcn﹣k（其中c，k为常数），且a2=4，a6=8a3．‎ ‎（1）求an；‎ ‎（2）求数列{nan}的前n项和Tn．‎ ‎18．（12分）如图，从A1（1，0，0），A2（2，0，0），B1（0，1，0，）B2（0，2，0），C1（0，0，1），C2（0，0，2）这6个点中随机选取3个点．‎ ‎（1）求这3点与原点O恰好是正三棱锥的四个顶点的概率；‎ ‎（2）求这3点与原点O共面的概率．‎ ‎19．（12分）如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=4，DE=4．现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG．‎ ‎（1）求证：平面DEG⊥平面CFG；‎ ‎（2）求多面体CDEFG的体积．‎ ‎20．（13分）已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足||=•（+）+2‎ ‎（1）求曲线C的方程；‎ ‎（2）点Q（x0，y0）（﹣2＜x0＜2）是曲线C上动点，曲线C在点Q处的切线为l，点P的坐标是（0，﹣1），l与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比．‎ ‎21．（14分）已知函数f（x）=（ax2+bx+c）ex在[0，1]上单调递减且满足f（0）=1，f（1）=0．‎ ‎（1）求a取值范围；‎ ‎（2）设g（x）=f（x）﹣f′（x），求g（x）在[0，1]上的最大值和最小值．‎ ‎　‎ ‎2012年江西省高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1．（5分）（2012•江西）若复数z=1+i（i为虚数单位） 是z的共轭复数，则z2+2的虚部为（　　）‎ A．0 B．﹣1 C．1 D．﹣2‎ ‎【分析】由z2+2 =（1+i）2+（1﹣i）2=2i﹣2i=0，由此得出结论．‎ ‎【解答】解：由题意可得 z2+2 =（1+i）2+（1﹣i）2=2i﹣2i=0，故z2+2的虚部为0，‎ 故选A．‎ ‎　‎ ‎2．（5分）（2012•江西）若全集U={x∈R|x2≤4}，则集合A={x∈R||x+1|≤1}的补集∁UA为（　　）‎ A．{x∈R|0＜x＜2|} B．{x∈R|0≤x＜2|} C．{x∈R|0＜x≤2|} D．{x∈R|0≤x≤2|}‎ ‎【分析】先一元二次不等式的解法以及带绝对值不等式的解法求出全集U以及集合A，再结合补集的定义求出结论．‎ ‎【解答】解：因为：全集U={x∈R|x2≤4}={x|﹣2≤x≤2}，‎ ‎∵|x+1|≤1⇒﹣1≤x+1≤1⇒﹣2≤x≤0，‎ ‎∴集合A={x∈R||x+1|≤1}={x|﹣2≤x≤0}，‎ 所以：∁UA={x|0＜x≤2}．‎ 故选：C．‎ ‎　‎ ‎3．（5分）（2012•江西）设函数f（x）=，则f（f（3））=（　　）‎ A． B．3 C． D．‎ ‎【分析】由条件求出f（3）=，结合函数解析式求出 f（f（3））=f（）=+1，计算求得结果．‎ ‎【解答】解：函数f（x）=，则f（3）=，‎ ‎∴f（f（3））=f（）=+1=，‎ 故选D．‎ ‎　‎ ‎4．（5分）（2012•江西）若=，则tan2α=（　　）‎ A．﹣ B． C．﹣ D．‎ ‎【分析】将已知等式左边的分子分母同时除以cosα，利用同角三角函数间的基本关系弦化切得到关于tanα的方程，求出方程的解得到tanα的值，然后将所求的式子利用二倍角的正切函数公式化简后，将tanα的值代入即可求出值．‎ ‎【解答】解：∵==，‎ ‎∴tanα=﹣3，‎ 则tan2α===．‎ 故选B ‎　‎ ‎5．（5分）（2012•江西）观察下列事实|x|+|y|=1的不同整数解（x，y）的个数为4，|x|+|y|=2的不同整数解（x，y）的个数为8，|x|+|y|=3的不同整数解（x，y）的个数为12 …．则|x|+|y|=20的不同整数解（x，y）的个数为（　　）‎ A．76 B．80 C．86 D．92‎ ‎【分析】观察可得不同整数解的个数可以构成一个首项为4，公差为4的等差数列，则所求为第20项，可计算得结果．‎ ‎【解答】‎ 解：观察可得不同整数解的个数4，8，12，…可以构成一个首项为4，公差为4的等差数列，‎ 通项公式为an=4n，则所求为第20项，所以a20=80‎ 故选B．‎ ‎　‎ ‎6．（5分）（2012•江西）小波一星期的总开支分布图如图1所示，一星期的食品开支如图2所示，则小波一星期的鸡蛋开支占总开支的百分比为（　　）‎ A．30% B．10% C．3% D．不能确定 ‎【分析】计算鸡蛋占食品开支的百分比，利用一星期的食品开支占总开支的百分比，即可求得一星期的鸡蛋开支占总开支的百分比 ‎【解答】解：根据一星期的食品开支图，可知鸡蛋占食品开支的百分比为%，‎ ‎∵一星期的食品开支占总开支的百分比为30%，‎ ‎∴一星期的鸡蛋开支占总开支的百分比为30%×10%=3%．‎ 故选：C．‎ ‎　‎ ‎7．（5分）（2012•江西）若一个几何体的三视图如图所示，则此几何体的体积为（　　）‎ A． B．5 C． D．4‎ ‎【分析】先根据三视图判断此几何体为直六棱柱，再分别计算棱柱的底面积和高，最后由棱柱的体积计算公式求得结果 ‎【解答】解：由图可知，此几何体为直六棱柱，底面六边形可看做两个全等的等腰梯形，上底边为1，下底边为3，高为1，‎ ‎∴棱柱的底面积为2×=4，‎ 棱柱的高为1‎ ‎∴此几何体的体积为V=4×1=4‎ 故选D ‎　‎ ‎8．（5分）（2012•江西）椭圆（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F1，F2．若|AF1|，|F1F2|，|F1B|成等比数列，则此椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎【分析】由题意可得，|AF1|=a﹣c，|F1F2|=2c，|F1B|=a+c，由|AF1|，|F1F2|，|F1B|成等比数列可得到e2==，从而得到答案．‎ ‎【解答】解：设该椭圆的半焦距为c，由题意可得，|AF1|=a﹣c，|F1F2|=2c，|F1B|=a+c，‎ ‎∵|AF1|，|F1F2|，|F1B|成等比数列，‎ ‎∴（2c）2=（a﹣c）（a+c），‎ ‎∴=，即e2=，‎ ‎∴e=，即此椭圆的离心率为．‎ 故选B．‎ ‎　‎ ‎9．（5分）（2012•江西）已知f（x）=sin2（x+），若a=f（lg5），b=f（lg），则（　　）‎ A．a+b=0 B．a﹣b=0 C．a+b=1 D．a﹣b=1‎ ‎【分析】由题意，可先将函数f（x）=sin2（x+）化为f（x）=，再解出a=f（lg5），b=f（lg）两个的值，对照四个选项，验证即可得到答案 ‎【解答】解：f（x）=sin2（x+）==‎ 又a=f（lg5），b=f（lg）=f（﹣lg5），‎ ‎∴a+b=+=1，a﹣b=﹣=sin2lg5‎ 故C选项正确 故选C ‎　‎ ‎10．（5分）（2012•江西）如图，|OA|=2（单位：m），OB=1（单位：m），OA与OB的夹角为，以A为圆心，AB为半径作圆弧与线段OA延长线交与点C．甲、乙两质点同时从点O出发，甲先以速度1（单位：m/s）沿线段OB行至点B，再以速度3（单位：m/s）沿圆弧行至点C后停止；乙以速率2（单位：m/s）沿线段OA行至A点后停止．设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）（S（0）=0），则函数y=S（t）的图象大致是（　　）‎ A． B． C． D．‎ ‎【分析】由题意，所围成的面积的变化可分为两段研究，一秒钟内与一秒钟后，由题设知第一秒内所围成的面积增加较快，一秒钟后的一段时间内匀速增加，一段时间后面积不再变化，由此规律可以选出正确选项 ‎【解答】解：由题设知，|OA|=2（单位：m），OB=1，两者行一秒后，甲行到B停止，乙此时行到A，故在第一秒内，甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）的值增加得越来越快，一秒钟后，随着甲的运动，所围成的面积增加值是扇形中AB所扫过的面积，由于点B是匀速运动，故一秒钟后，面积的增加是匀速的，且当甲行走到C后，即B与C重合后，面积不再随着时间的增加而改变，故函数y=S（t）随着时间t的增加先是增加得越来越快，然后转化成匀速增加，然后面积不再变化，考察四个选项，只有A符合题意 故选A ‎　‎ 二、填空题：本大题共5小题，每小题5分，共25分．‎ ‎11．（5分）（2012•江西）不等式的解集是　{x|﹣3＜x＜2 或x＞3}　．‎ ‎【分析】由不等式可得 （x﹣2）（x2﹣9）＞0，由此解得不等式的解集．‎ ‎【解答】解：由不等式可得 （x﹣2）（x2﹣9）＞0，解得﹣3＜x＜2 或x＞3，‎ 故不等式的解集为 {x|﹣3＜x＜2 或x＞3}，‎ 故答案为：{x|﹣3＜x＜2 或x＞3}．‎ ‎　‎ ‎12．（5分）（2012•江西）设单位向量=（x，y），=（2，﹣1）．若⊥，则|x+2y|=　　．‎ ‎【分析】由题意，可由题设条件单位向量=（x，y）及⊥，建立关于x，y的方程组，解出x，y的值，从而求出|x+2y|得到答案 ‎【解答】解：由题意，单位向量=（x，y），=（2，﹣1）．且⊥，‎ ‎∴，解得x=±，y=±，‎ ‎∴|x+2y|=‎ 故答案为 ‎　‎ ‎13．（5分）（2012•江西）等比数列{an}的前n项和为Sn，公比不为1．若a1=1，且对任意的n∈N+都有an+2+an+1﹣2an=0，则S5=　11　．‎ ‎【分析】由题意可得anq2+an q=2an ，即 q2+q=2，解得 q=﹣2，或 q=1（舍去），由此求得 S5= 的值．‎ ‎【解答】解：∵等比数列{an}的前n项和为Sn，a1=1，且对任意的n∈N+都有an+2+an+1﹣2an=0，∴anq2+anq=2an ，‎ 即 q2+q=2，解得 q=﹣2，或 q=1（舍去）．‎ ‎∴S5==11，‎ 故答案为 11．‎ ‎　‎ ‎14．（5分）（2012•江西）过直线x+y﹣2=0上点P作圆x2+y2=1的两条切线，若两条切线的夹角是60°，则点P的坐标是　（，）　．‎ ‎【分析】根据题意画出相应的图形，设P的坐标为（a，b），由PA与PB为圆的两条切线，根据切线的性质得到OA与AP垂直，OB与BP垂直，再由切线长定理得到PO为角平分线，根据两切线的夹角为60°，求出∠APO和∠‎ BPO都为30°，在直角三角形APO中，由半径AO的长，利用30°角所对的直角边等于斜边的一半求出OP的长，由P和O的坐标，利用两点间的距离公式列出关于a与b的方程，记作①，再由P在直线x+y﹣2=0上，将P的坐标代入得到关于a与b的另一个方程，记作②，联立①②即可求出a与b的值，进而确定出P的坐标．‎ ‎【解答】解：根据题意画出相应的图形，如图所示：‎ 直线PA和PB为过点P的两条切线，且∠APB=60°，‎ 设P的坐标为（a，b），连接OP，OA，OB，‎ ‎∴OA⊥AP，OB⊥BP，PO平分∠APB，‎ ‎∴∠OAP=∠OBP=90°，∠APO=∠BPO=30°，‎ 又圆x2+y2=1，即圆心坐标为（0，0），半径r=1，‎ ‎∴OA=OB=1，‎ ‎∴OP=2AO=2BO=2，∴=2，即a2+b2=4①，‎ 又P在直线x+y﹣2=0上，∴a+b﹣2=0，即a+b=2②，‎ 联立①②解得：a=b=，‎ 则P的坐标为（，）．‎ 故答案为：（，）‎ ‎　‎ ‎15．（5分）（2012•江西）下图是某算法的程序框图，则程序运行后输出的结果是　3　．‎ ‎【分析】直接计算循环后的结果，当k=6时不满足判断框的条件，推出循环输出结果即可．‎ ‎【解答】解：第1次，满足循环，a=1，T=1，K=2，第2次满足2＜6；sin，不成立，‎ 执行a=0，T=1，k=3，第3次有，不满足条件循环，‎ a=0，T=1，k=4，满足，a=1，T=2，k=5，满足k＜6，‎ 此时成立，a=1，T=3，k=6，不满足6＜6，退出循环，输出结果T=3．‎ 故答案为：3．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎16．（12分）（2012•江西）△ABC中，角A，B，C的对边分别为a，b，c．已知3cos（B﹣C）﹣1=6cosBcosC．‎ ‎（1）求cosA；‎ ‎（2）若a=3，△ABC的面积为，求b，c．‎ ‎【分析】（1）利用两角和与差的余弦函数公式化简已知等式左边的第一项，移项合并后再利用两角和与差的余弦函数公式得出cos（B+C）的值，将cosA用三角形的内角和定理及诱导公式变形后，将cos（B+C）的值代入即可求出cosA的值；‎ ‎（2）由cosA的值及A为三角形的内角，利用同角三角函数间的基本关系求出sinA的值，利用三角形的面积公式表示出三角形ABC的面积，将已知的面积及sinA的值代入，得出bc=6，记作①，再由a及cosA的值，利用余弦定理列出关于b与c的关系式，记作②，联立①②即可求出b与c的值．‎ ‎【解答】解：（1）3cos（B﹣C）﹣1=6cosBcosC，‎ 化简得：3（cosBcosC+sinBsinC）﹣1=6cosBcosC，‎ 变形得：3（cosBcosC﹣sinBsinC）=﹣1，‎ 即cos（B+C）=﹣，‎ 则cosA=﹣cos（B+C）=；‎ ‎（2）∵A为三角形的内角，cosA=，‎ ‎∴sinA==，‎ 又S△ABC=2，即bcsinA=2，解得：bc=6①，‎ 又a=3，cosA=，‎ ‎∴由余弦定理a2=b2+c2﹣2bccosA得：b2+c2=13②，‎ 联立①②解得：或．‎ ‎　‎ ‎17．（12分）（2012•江西）已知数列{an}的前n项和Sn=kcn﹣k（其中c，k为常数），且a2=4，a6=8a3．‎ ‎（1）求an；‎ ‎（2）求数列{nan}的前n项和Tn．‎ ‎【分析】（1）先根据前n项和求出数列的通项表达式；再结合a2=4，a6=8a3求出c，k，即可求出数列的通项；‎ ‎（2）直接利用错位相减法求和即可．‎ ‎【解答】解：（1）由Sn=kcn﹣k，得an=sn﹣sn﹣1=kcn﹣kcn﹣1； （n≥2），‎ 由a2=4，a6=8a3．得kc（c﹣1）=4，kc5（c﹣1）=8kc2（c﹣1），解得；‎ 所以a1=s1=2；‎ an=sn﹣sn﹣1=kcn﹣kcn﹣1=2n，（n≥2），‎ 于是an=2n．‎ ‎（2）：∵nan=n•2n；‎ ‎∴Tn=2+2•22+3•23+…+n•2n；‎ ‎ 2Tn=22+2•23+3•24+…+（n﹣1）•2n+n•2n+1；‎ ‎∴﹣Tn=2+22+23…+2n﹣n•2n+1=﹣n•2n+1=﹣2+2n+1﹣n•2n+1；‎ 即：Tn=（n﹣1）•2n+1+2．‎ ‎　‎ ‎18．（12分）（2012•江西）如图，从A1（1，0，0），A2（2，0，0），B1（0，1，0，）B2（0，2，0），C1（0，0，1），C2（0，0，2）这6个点中随机选取3个点．‎ ‎（1）求这3点与原点O恰好是正三棱锥的四个顶点的概率；‎ ‎（2）求这3点与原点O共面的概率．‎ ‎【分析】根据题意，分情况讨论，列举可得从6点中随机取出3个点的情况数目，‎ ‎（1）由正三棱锥的定义，在列举的结果中分析可得选取的3点与原点O恰好是正三棱锥的四个顶点的情况数目，由等可能事件的概率公式，计算可得答案；‎ ‎（2）根据题意，在列举的结果中分析可得选取的3点与原点O共面的情况数目，由等可能事件的概率公式，计算可得答案．‎ ‎【解答】解：从这6点中随机取出3个点，其所有的情况有 x轴上取2个点的有A1A2B1，A1A2B2，A1A2C1，A1A2C2，共4种情况，‎ y轴上取2个点的有B1B2A1，B1B2A2，B1B2C1，B1B2C2，共4种情况，‎ Z轴上取2个点的有C1C2A1，C1C2A2，C1C2B1，C1C2B2，共4种情况，‎ ‎3个点在不同的坐标轴上有A1B1C1，A1B1C2，A1B2C1，A1B2C2，A2B1C1，A2B1C2，A2B2C1，A2B2C2，共8种情况，‎ 则从这6点中随机取出3个点，其所有的情况共有4+4+4+12=20种，‎ ‎（1）选取的3点与原点O恰好是正三棱锥的四个顶点的情况有A1B1C1，A2B2C2，共2种，‎ 则其概率P1==，‎ ‎（2）选取的3点与原点O共面的情况，有A1A2B1，A1A2B2，A1A2C1，A1A2C2，B1B2A1，B1B2A2，B1B2C1，B1B2C2，C1C2A1，C1C2A2，C1C2B1，C1C2B2，共12种，‎ 则选取的3点与原点O共面的概率P2==．‎ ‎　‎ ‎19．（12分）（2012•江西）如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=4，DE=4．现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG．‎ ‎（1）求证：平面DEG⊥平面CFG；‎ ‎（2）求多面体CDEFG的体积．‎ ‎【分析】（1）判断四边形CDEF为矩形，然后证明EG⊥GF，推出CF⊥EG，然后证明平面DEG⊥平面CFG．‎ ‎（2）在平面EGF中，过点G作GH⊥EF于H，求出GH，说明GH⊥平面CDEF，利用求出体积．‎ ‎【解答】解：（1）证明：因为DE⊥EF，CF⊥EF，所以四边形CDEF为矩形，‎ 由AD=5，DE=4，得AE=GE==3，‎ 由GC=4，CF=4，得BF=FG==4，所以EF=5，‎ 在△EFG中，有EF2=GE2+FG2，所以EG⊥GF，‎ 又因为CF⊥EF，CF⊥FG，得CF⊥平面EFG，‎ 所以CF⊥EG，所以EG⊥平面CFG，即平面DEG⊥平面CFG．‎ ‎（2）解：在平面EGF中，过点G作GH⊥EF于H，则GH==，‎ 因为平面CDEF⊥平面EFG，得GH⊥平面CDEF，‎ ‎=16．‎ ‎　‎ ‎20．（13分）（2012•江西）已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足||=•（+）+2‎ ‎（1）求曲线C的方程；‎ ‎（2）点Q（x0，y0）（﹣2＜x0＜2）是曲线C上动点，曲线C在点Q处的切线为l，点P的坐标是（0，﹣1），l与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比．‎ ‎【分析】（1）先求出、的坐标，由此求得||和•（+）+2的值，由题意可得 =4﹣2y，化简可得所求．‎ ‎（2）根据直线PA，PB的方程以及曲线C在点Q（x0，y0）（﹣2＜x0＜2）处的切线方程，求出F点的坐标，D、E两点的横坐标，可得S△PDE和S△QAB的值，从而求得△QAB与△PDE的面积之比．‎ ‎【解答】解：（1）由=（﹣2﹣x，1﹣y），=（2﹣x，1﹣y）可得=（﹣2x，2﹣2y），‎ ‎∴||=，•（+）+2=（x，y）•（0，2）+2=2+2y．‎ 由题意可得 =2+2y，化简可得 x2 =4y．‎ ‎（2）由题意可得直线PA，PB的方程分别为 y=﹣x﹣1、y=x﹣1，且y0 =x0，‎ 曲线C在点Q（x0，y0）（﹣2＜x0＜2）处的切线斜率为k=x0，‎ ‎∴曲线C在点Q（x0，y0）（﹣2＜x0＜2）处的切线方程为y=x0x﹣，‎ 且与y轴的交点F（0，﹣）．‎ 由 求得xD=，由求得xE=．‎ 故xE﹣xD=2，故|FP|=1﹣．‎ 故S△PDE=|PF|•|xE﹣xD|=（1﹣）•2=，‎ 而S△QAB=×4×（1﹣）=，‎ ‎∴=2，即△QAB与△PDE的面积之比等于2．‎ ‎　‎ ‎21．（14分）（2012•江西）已知函数f（x）=（ax2+bx+c）ex在[0，1]上单调递减且满足f（0）=1，f（1）=0．‎ ‎（1）求a取值范围；‎ ‎（2）设g（x）=f（x）﹣f′（x），求g（x）在[0，1]上的最大值和最小值．‎ ‎【分析】（1）由题意，函数f（x）=（ax2+bx+c）ex在[0，1]上单调递减且满足f（0）=1，f（1）=0，可求出函数的导数，将函数在[0，1]上单调递减转化为导数在[0，1]上的函数值恒小于等于0，再结合f（0）=1，f（1）=0这两个方程即可求得a取值范围；‎ ‎（2）由题设条件，先给出g（x）=f（x）﹣f′（x）的解析式，求出导函数，g′（x）=（﹣2ax﹣a+1）ex，由于参数a的影响，函数在[0，1]上的单调性不同，结合（1）的结论及g′（x）可得．‎ ‎（i）当a=0时；（ii）当a=1时；（iii）当0＜a＜1时，分三类对函数的单调性进行讨论，确定并求出函数的最值 ‎【解答】解：（1）由f（0）=1，f（1）=0得c=1，a+b=﹣1，则f（x）=[ax2‎ ‎﹣（a+1）x+1]ex，‎ ‎∴f′（x）=[ax2+（a﹣1）x﹣a]ex，‎ 由题意函数f（x）=（ax2+bx+c）ex在[0，1]上单调递减可得对于任意的x∈（0，1），都有f′（x）≤0‎ 当a＞0时，因为二次函数y=ax2+（a﹣1）x﹣a图象开口向上，而f′（0）=﹣a＜0，所以只需要f′（1）=（a﹣1）e≤0，即a≤1，故有0＜a≤1；‎ 当a=1时，对于任意的x∈（0，1），都有f′（x）=（x2﹣1）ex＜0，函数符合条件；‎ 当a=0时，对于任意的x∈（0，1），都有f′（x）=﹣xex＜0，函数符合条件；‎ 当a＜0时，因f′（0）=﹣a＞0函数不符合条件；‎ 综上知，a的取值范围是0≤a≤1‎ ‎（2）因为 g（x）=f（x）﹣f′（x）=（ax2﹣（a+1）x+1）ex﹣[ax2+（a﹣1）x﹣a]ex=（﹣2ax+a+1）ex，g′（x）=（﹣2ax﹣a+1）ex，‎ ‎（i）当a=0时，g′（x）=ex＞0，g（x）在[0，1]上的最小值是g（0）=1，最大值是g（1）=e ‎（ii）当a=1时，对于任意x∈（0，1）有g′（x）=﹣2xex＜0，则有g（x）在[0，1]上的最小值是g（1）=0，最大值是g（0）=2；‎ ‎（iii）当0＜a＜1时，由g′（x）=0得x=＞0，‎ ‎①若，即0＜a≤时，g（x）在[0，1]上是增函数，所以g（x）在[0，1]上最大值是g（1）=（1﹣a）e，最小值是g（0）=1+a；‎ ‎②若，即＜a＜1时，g（x）在x=取得最大值g（）=2a，在x=0或x=1时取到最小值，‎ 而g（0）=1+a，g（1）=（1﹣a）e，‎ 则令g（0）=1+a≤g（1）=（1﹣a）e可得＜a≤；令g（0）=1+a≥g（1）=（1﹣a）e可得≤a＜1‎ 综上，当＜a≤时，g（x）在x=0取到最小值g（0）=1+a，‎ 当≤a＜1时，g（x）在x=1取到最小值g（1）=（1﹣a）e ‎　‎ 参与本试卷答题和审题的老师有：caoqz；庞会丽；sllwyn；zwx097；刘长柏；xize；wfy814；xintrl；qiss；danbo7801（排名不分先后）‎ ‎2017年2月3日