2018-2019学年陕西省西安市长安区第一中学高一上学期第二次月考数学试题（解析版）

2018-2019学年陕西省西安市长安区第一中学高一上学期第二次月考数学试题（解析版）

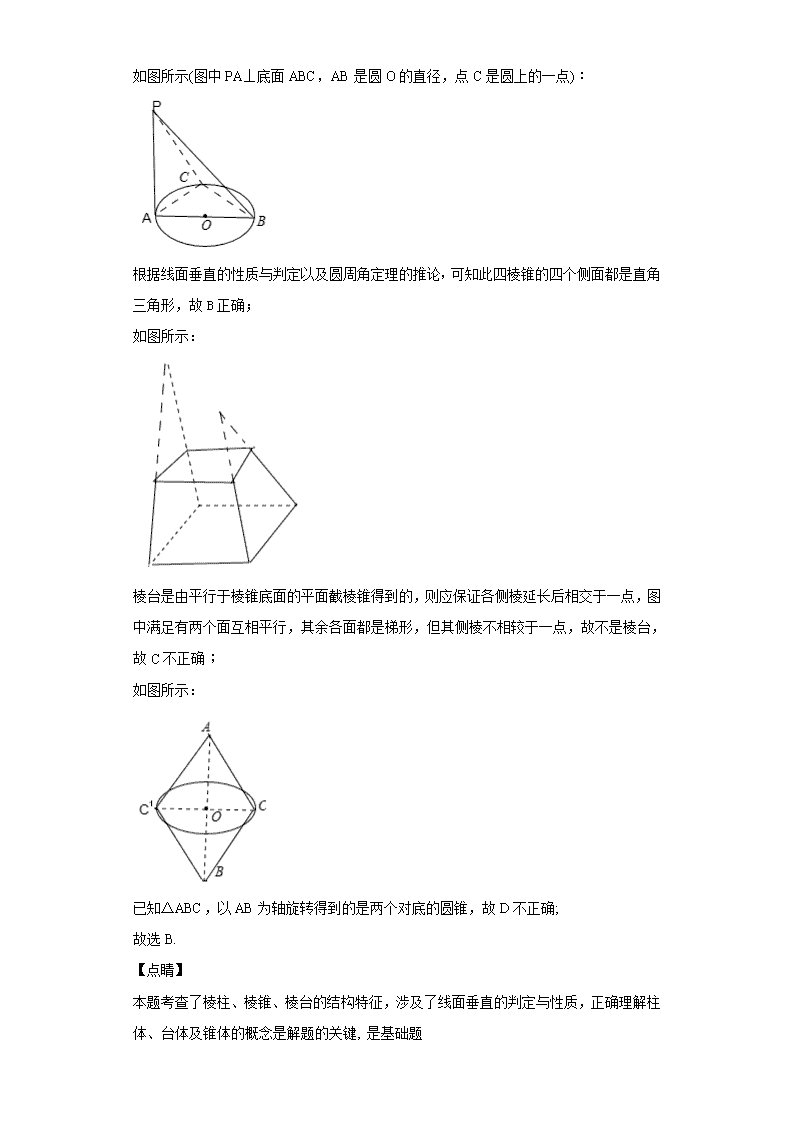
‎2018-2019学年陕西省西安市长安区第一中学高一上学期第二次月考数学试题 一、单选题 ‎1．函数的定义域为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】根据对数的真数大于0以及二次根式有意义的条件，求解函数的定义域.‎ ‎【详解】‎ 由函数，可知 ，解得 ，‎ 故选B ‎【点睛】‎ 本题考查了求函数的定义域问题，已知解析式中同时出现对数函数式与二次根式时，分别求出它们各自的定义域，然后求交集即可,是基础题.‎ ‎2．下列说法正确的是( 　)‎ A．有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱 B．四棱锥的四个侧面都可以是直角三角形 C．有两个面互相平行，其余各面都是梯形的多面体是棱台 D．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥 ‎【答案】B ‎【解析】通过举出反例可判断A,C,D错误，找到符合B条件的图形，即可得出答案.‎ ‎【详解】‎ 如图所示：‎ 满足有两个平面互相平行，其余各面都是平行四边形，但不是棱柱，故A不正确；‎ 如图所示(图中PA⊥底面ABC，AB是圆O的直径，点C是圆上的一点)：‎ 根据线面垂直的性质与判定以及圆周角定理的推论，可知此四棱锥的四个侧面都是直角三角形，故B正确；‎ 如图所示：‎ 棱台是由平行于棱锥底面的平面截棱锥得到的，则应保证各侧棱延长后相交于一点，图中满足有两个面互相平行，其余各面都是梯形，但其侧棱不相较于一点，故不是棱台，故C不正确；‎ 如图所示：‎ 已知△ABC，以AB为轴旋转得到的是两个对底的圆锥，故D不正确;‎ 故选B.‎ ‎【点睛】‎ 本题考查了棱柱、棱锥、棱台的结构特征，涉及了线面垂直的判定与性质，正确理解柱体、台体及锥体的概念是解题的关键, 是基础题 ‎3．下列选项中，表示的是同一函数的是（ ）‎ A．与 B．与 C．与 D．与 ‎【答案】C ‎【解析】若两个函数的定义域相同，对应关系也相同，即可判断是同一函数.‎ ‎【详解】‎ A中= ，定义域为 ,=,定义域为R;‎ B中的定义域为， ，其定义域为{x|} ；‎ C中的定义域为R，=，其定义域也为R;‎ D中=x-1，定义域为，的定义域为R;‎ 即C中两个函数定义域相同，对应关系也相同是同一函数.‎ 故选C.‎ ‎【点睛】‎ 本题考查了判断两个函数是否为同一函数，一般方法是：变形化简函数的表达式，判断两个函数的定义域是否相同，对应法则是否也相同 ‎4．球面上有四个点，若两两垂直，且，则该球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】分析：首先求得外接球半径，然后求解其表面积即可.‎ 详解：由题意可知，该球是一个棱长为4的正方体的外接球，‎ 设球的半径为，由题意可得：,‎ 据此可得：，外接球的表面积为：.‎ 本题选择D选项.‎ 点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.‎ ‎5．已知函数在上单调递减，则的取值范围是（　 ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】对函数求导，函数在上单调递减，则导数在上导数小于等于，当时，，恒小于，符合题意；当时，因函导数是一次函数，故只有，且最小值为，，故选C.‎ ‎6．如图在三棱锥中,E､F是棱AD上互异的两点,G､H是棱BC上互异的两点,由图可知 ‎①AB与CD互为异面直线;②FH分别与DC､DB互为异面直线;‎ ‎③EG与FH互为异面直线;④EG与AB互为异面直线.‎ 其中叙述正确的是 ( )‎ A.①③ B.②④ C.①②④ D.①②③④‎ ‎【答案】A ‎【解析】试题分析：①AB与CD互为异面直线，正确；②当点F与点D重合时，FH分别与DC､DB就不为异面直线；③EG与FH互为异面直线，正确；④当点E与点A重合时，EG与AB不为异面直线.‎ ‎【考点】异面直线。‎ 点评：在做本题时要注意点的特殊性；尤其是E、F、G、H、为端点的情况。因此我们在做题时要考虑全面。属于有中档题。‎ ‎7．已知是奇函数，是偶函数，且，则等于( )‎ A．6 B．5 C．4 D．3‎ ‎【答案】B ‎【解析】利用函数的奇偶性，得到关于f（1）与g（1）的方程组，进而求解.‎ ‎【详解】‎ 由f（x）是奇函数，g（x）是偶函数，可知f（-x）= -f（x），g（-x）=g（x），‎ 由f（-1）+g（1）=4，f（1）+g（-1）=6，‎ 可得-f（1）+g（1）=4，f（1）+g（1）=6，解得g（1）=5．‎ 故选B.‎ ‎【点睛】‎ 本题考查了函数的奇偶性的应用；偶函数 f（-x）=f（x），奇函数f（-x）= -f（x），解答本题的关键是利用函数的奇偶性构造出关于f（1）与g（1）的方程组.‎ ‎8．一个几何体的三视图如图所示，则该几何体的体积为（ ） ‎ A． B． C． D．‎ ‎【答案】D ‎【解析】考查三视还原直观图的能力及体积的计算。由三视图可知几何体为下层半径为1同1的圆柱，圆柱上面放一底面斜边为2的等腰直角三角形高为的三棱锥，故：‎ ‎9．函数的图象大致是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】根据函数的奇偶性，结合特殊点的值的情况求解.‎ ‎【详解】‎ 已知函数，==‎ ‎，即函数是偶函数，故排除选项B，D;‎ 由，得或 ，‎ 当x>0时， ，，‎ 可排除选项C，故选A.‎ ‎【点睛】‎ 本题考查了已知函数表达式，识别函数图象，涉及了函数的零点与函数的奇偶性；从函数的奇偶性可以判断函数图象的对称性，从特殊点的值的情况，可以排除不符合要求的选项.‎ ‎10．设， 是两条不同的直线， 是一个平面，则下列命题正确的是 （ ）‎ A．若， ，则 B．若， ，则 C．若， ，则 D．若， ，则 ‎【答案】B ‎【解析】试题分析： ，则垂直内所有直线，故A正确；B错， 可能在内；C错， 与可能异面，D错， 与可能相交.‎ ‎【考点】线面的位置关系 ‎11．已知正方形的对角线与相交于点，将沿对角线折起，使得平面平面（如图），则下列命题中正确的是（ ）‎ A．直线直线，且直线直线 B．直线平面，且直线平面 C．平面平面，且平面平面 D．平面平面，且平面平面 ‎【答案】C ‎【解析】分析：由题意结合几何关系逐一考查所给命题的真假即可求得最终结果.‎ 详解：若，则AB在平面ACD内的射影AC⊥CD，该结论明显不成立，则直线 AB⊥直线CD不成立，故A错误；‎ ‎∵AB与CD不垂直，所以直线AB⊥平面BCD不成立，故B错误；‎ ‎∵AC⊥DE，BE⊥AC，∴AC⊥平面BDE，∴平面ABC上平面BDE，‎ 且平面ACD⊥平面BDE，故C正确；‎ 很明显平面ABD⊥平面BCD不成立，故D错误.‎ 本题选择C选项.‎ 点睛：本题主要考查线面关系的命题及其应用等知识，意在考查学生的转化能力和计算求解能力.‎ ‎12．对于定义域为R的函数，若存在非零实数，使函数在和上与x轴都有交点，则称为函数的一个“界点”.则下列四个函数中，不存在“界点”的是（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】根据“界点”的定义，可知函数存在两个及两个以上零点时，函数存在“界点”.‎ ‎【详解】‎ A中f（x）=2x-x2，当x=2，x=4时f（x）=0，因此可知，在（2，4）之间存在“界点”；‎ B中，由可知其图象恒与x轴有两个交点，故存在“界点”；‎ C中 = ，其图象与x轴有两个交点（1，0），（3，0），故存在“界点”；‎ D中 的图象与x轴只有一个交点，故D不存在“界点”．‎ 故选D.‎ ‎【点睛】‎ 本题以新定义为载体，考查了函数的零点，求函数的零点的常用方法有：直接法，函数性质法，转化法和数形结合法.‎ 二、填空题 ‎13．一个水平放置的平面图形的斜二测直观图是一个底角为 ‎,腰和上底均为1的等腰梯形，则这个平面图形的面积是________．‎ ‎【答案】 ‎ ‎【解析】根据斜二测画法还原出原平面图形，进而求出它的面积.‎ ‎【详解】‎ 把直观图还原出原平面图形，如图所示；‎ ‎∴这个平面图形是直角梯形，它的面积为 ,‎ 故填：.‎ ‎【点睛】‎ 本题考查了斜二测画法画直观图的应用问题，解题的关键是还原出原平面图形,原图形中平行于x轴的线段，在直观图中保持原长度不变；平行于y轴的线段，长度为原来的一半.‎ ‎14．设函数，则使得成立的的取值范围是 .‎ ‎【答案】.‎ ‎【解析】试题分析：x＜1时，，∴，∴x＜1；x≥1时，，∴x≤8，∴1≤x≤8，‎ 综上，使得f（x）≤2成立的x的取值范围是x≤8．故答案为：．‎ ‎【考点】1．其他不等式的解法；2．分段函数的解析式求法及其图象的作法．‎ ‎15．已知集合，，则集合A，B之间的关系为________．‎ ‎【答案】A=B ‎【解析】分别讨论k=2n和k=2n-1，n∈Z时，集合A所表示的集合，由描述法的定义即可知道集合A=B.‎ ‎【详解】‎ 对于集合A，k=2n时， ，‎ 当k=2n-1时，‎ 即集合A= ,由B=‎ 可知A=B，故填：A=B.‎ ‎【点睛】‎ 本题考查了集合之间的关系，考查了集合相等的判断，涉及了集合的表示法，是基础题.‎ ‎16．如图，在正方体中，过对角线的一个平面交于点，交于.‎ ‎①四边形一定是平行四边形；‎ ‎②四边形有可能是正方形；‎ ‎③四边形在底面内的投影一定是正方形；‎ ‎④四边形有可能垂直于平面．‎ 以上结论正确的为_______________．（写出所有正确结论的编号）‎ ‎【答案】①③④‎ ‎【解析】分析：由题意结合几何关系逐一考查所给命题的真假即可求得最终结果.‎ 详解：如图所示：‎ ‎①由于平面BCB1C1∥平面ADA1D1，并且B、E、F、D1，四点共面，故ED1∥BF，‎ 同理可证，FD1∥EB，故四边形BFD1E一定是平行四边形，故①正确；‎ ‎②若BFD1E是正方形，有ED1⊥BE，结合A1D1⊥BE可得BE⊥平面ADD1A1，明显矛盾，故②错误；‎ ‎③由图得，BFD1E在底面ABCD内的投影一定是正方形ABCD，故③正确；‎ ‎④当点E和F分别是对应边的中点时，EF⊥平面BB1D，则平面BFD1E⊥平面BB1D，故④正确.‎ 综上可得：题中所给的结论正确的为①③④.‎ 点睛：本题考查了空间几何体的线面位置关系判定与证明：‎ ‎（1）对于异面直线的判定要熟记异面直线的概念：把既不平行也不相交的两条直线称为异面直线；‎ ‎（2）对于线面位置关系的判定中，熟记线面平行与垂直、面面平行与垂直的定理是关键.‎ 三、解答题 ‎17．已知集合，.‎ ‎（1）求集合；‎ ‎（2）若，求实数的取值范围.‎ ‎【答案】（1）；（2）。‎ ‎【解析】（1）求解指数不等式，能求出集合A．‎ ‎（2）由A={x|﹣4≤x≤3}，B={x|m+1≤x≤3m﹣1}，B⊆A，当B=∅时，m+1＞3m﹣1，当B≠∅时，列出不等式组，由此能求出实数m的取值范围．‎ ‎【详解】‎ ‎（1）∵，∴2﹣3≤2x+1≤24，‎ ‎∴﹣3≤x+1≤4，解得﹣4≤x≤3，‎ ‎∴集合A={x|≤2x+1≤16}={x|﹣4≤x≤3}．‎ ‎（2）∵A={x|﹣4≤x≤3}，B={x|m+1≤x≤3m﹣1}，B⊆A，‎ ‎∴当B=∅时，m+1＞3m﹣1，解得m＜1，满足题意；‎ 当B≠∅时，，解得1≤m≤．‎ 综上，实数m的取值范围是（﹣∞，]．‎ ‎【点睛】‎ 防范空集.在解决有关A∩B＝∅，A⊆B等集合问题时，往往忽略空集的情况，一定先考虑∅是否成立，以防漏解.‎ ‎18．设，且 ．‎ ‎（1）求的值及的定义域；‎ ‎（2）求在区间 上的值域．‎ ‎【答案】（1）（2）‎ ‎【解析】试题分析：（1）由可求出，由对数的真数为正数，即可求函数的定义域；（2）由及复合函数的单调性可知，当时，是增函数；当时，是减函数，由单调性可求值域.‎ 试题解析：（1）∵，∴，∴．‎ 由，得，∴函数的定义域为 ‎（2），‎ ‎∴当时，是增函数；当时，是减函数，‎ 函数在上的最大值是，‎ 函数在上的最小值是，‎ ‎∴在区间上的值域是．‎ ‎【考点】1.对数函数的图象与性质；2.复合函数的单调性.‎ ‎19．如图所示，为平行四边形ABCD所在平面外一点，M,N分别为AB,PC的中点，平面PAD平面PBC＝.‎ ‎(1)求证：BC∥； ‎ ‎(2)MN与平面PAD是否平行？试证明你的结论．‎ ‎【答案】（1）见解析；（2）见解析 ‎【解析】试题分析：证明线线平行的方法；1，向量法，2.垂直于同一平面的两条直线平行，3平行于同一直线的两条直线平行，4一个平面与另外两个平行平面相交,那么两条交线也平行。线面平行，1平面外的一条直线与平面内的一条直线平行，则这条直线与这个平面平行，2若一条直线与一个平面同时平行于另一个平面且这条直线不属于这个平面，则这条直线与这个平面平行，3若一条直线与两平行平面中的一个平行，则这条直线与另一个平面平行，4，最好用的还是向量法。‎ 试题解析：(1)证明 因为BC∥AD，AD⊂平面PAD，‎ BC⊄平面PAD，所以BC∥平面PAD.‎ 又平面PAD∩平面PBC＝l，BC⊂平面PBC，所以BC∥l.‎ ‎(2)解 MN∥平面PAD.证明如下：‎ 如图所示，取PD中点E，连结AE，EN.‎ 又∵N为PC的中点，∴‎ 又∵‎ ‎∴‎ 即四边形AMNE为平行四边形．‎ ‎∴AE∥MN，又MN⊄平面PAD，AE⊂平面PAD ‎.∴MN∥平面PAD.‎ ‎【考点】线面平行的性质定理及判断定理 ‎20．如图，在三棱锥中，，为线段 的中点，为线段上一点.‎ ‎（1）求证：；‎ ‎（2）求证：平面平面；‎ ‎（3）当平面时，求三棱锥的体积.‎ ‎【答案】（1）证明见解析；（2）证明见解析；（3）.‎ ‎【解析】【详解】‎ 分析：（1）因为所以平面，又因为平面，所以；（2）由等腰三角形的性质可得 ，由（1）知，，所以平面，从而平面平面；（3）先证明，结合（1）可得平面，从而可得三棱锥的体积为，进而可得结果.‎ 详解：（1）因为PA⊥AB，PA⊥BC，所以PA⊥平面ABC.‎ 又因为BD平面ABC，所以PA⊥BD.‎ ‎（2）因为AB=BC，D为AC中点，所以BD⊥AC. ‎ 由（1）知，PA⊥BD，所以BD⊥平面PAC，‎ 所以平面BDE⊥平面PAC.‎ ‎（3）因为PA∥平面BDE，平面PAC平面BDE=DE，‎ 所以PA∥DE.‎ 因为D为AC的中点，所以DE=PA=l，BD=DC=.‎ 由（1）知，PA⊥平面ABC，所以DE⊥平面ABC,‎ 所以三棱锥E-BCD的体积V=BD·DC·DE=.‎ 点睛：本题主要考查线面垂直的判定定理及面面垂直的判定定理，属于难题.解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.‎ ‎21．已知定义域为的函数是奇函数.‎ ‎（1）求实数的值；‎ ‎（2）判断的单调性并用定义证明；‎ ‎（3）已知不等式恒成立, 求实数的取值范围.‎ ‎【答案】（1）； （2）减函数，证明见解析； （3） .‎ ‎【解析】（1）根据奇函数的定义域若存在x=0，则f（0）=0，求解参数的值；‎ ‎（2）结合y=2x的性质，通过证明任意，有，证明函数是减函数；‎ ‎（3）根据函数的奇偶性，将不等式恒成立转化为不等式恒成立，再结合函数的单调性求解.‎ ‎【详解】‎ ‎（1）是上的奇函数,， 得 ‎（2）减函数，证明如下：‎ 设是上任意两个实数，且，‎ ‎ ‎ ‎ ，即， ，‎ ‎，即，在上是减函数 ‎（3）不等式恒成立，‎ 是奇函数，即不等式恒成立 ‎ 又 在上是减函数，不等式恒成立 ‎ 当时，得 ‎ ‎ 当时，得 ‎ ‎ 综上，实数的取值范围是 ‎【点睛】‎ 本题考查了函数的奇偶性与单调性，考查了不等式恒成立问题，考查了应用对数函数单调性解与对数有关的不等式，涉及了指数函数与对数函数的图象与性质，体现了转化思想在解题中的运用 .‎