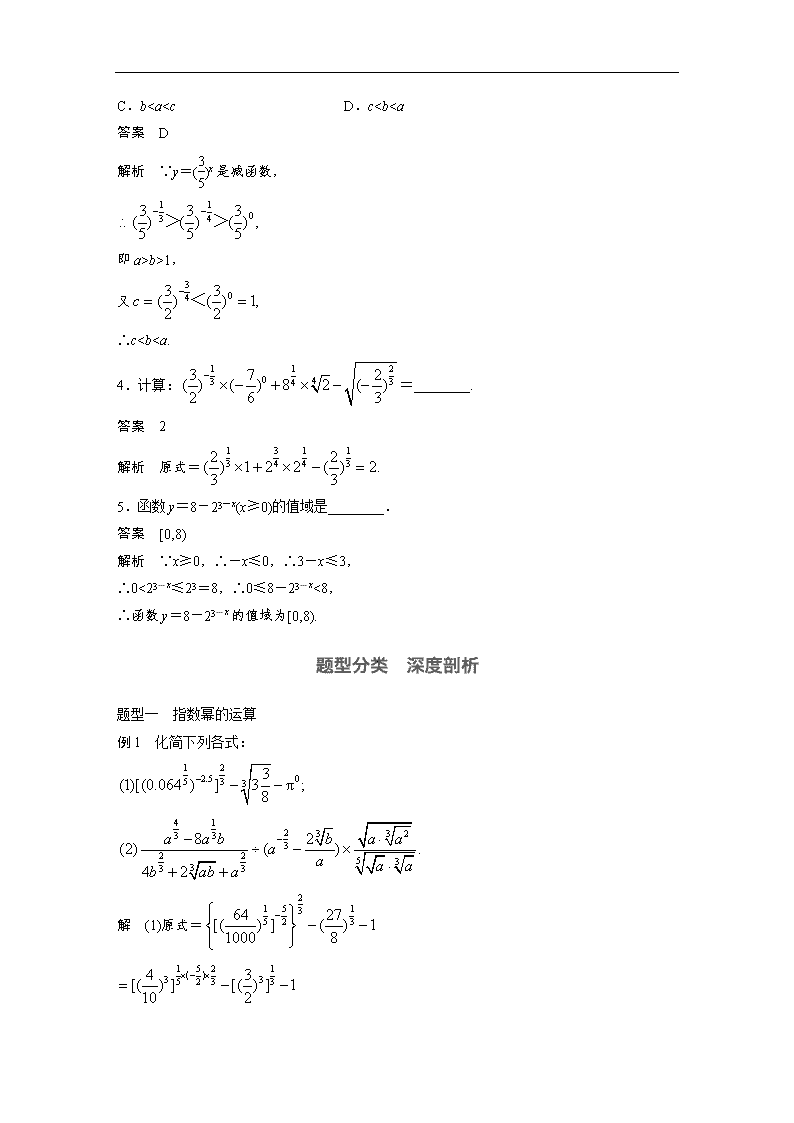高考数学专题复习练习:第二章 2_5分数指数幂
1.分数指数幂
(1)我们规定正数的正分数指数幂的意义是=(a>0,m,n∈N*,且n>1).于是,在条件a>0,m,n∈N*,且n>1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定=(a>0,m,n∈N*,且n>1).0的正分数指数幂等于0;0的负分数指数幂没有意义.
(2)有理数指数幂的运算性质:aras=ar+s,(ar)s=ars,(ab)r=arbr,其中a>0,b>0,r,s∈Q.
2.指数函数的图象与性质
y=ax
a>1
0
0时,y>1;
当x<0时,00时,01
(6)在(-∞,+∞)上是增函数
(7)在(-∞,+∞)上是减函数
【知识拓展】
1.指数函数图象画法的三个关键点
画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),(-1,).
2.指数函数的图象与底数大小的比较
如图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,底数a,b,c,d与1之间的大小关系为c>d>1>a>b.由此我们可得到以下规律:在第一象限内,指数函数y=ax(a>0,且a≠1)的图象越高,底数越大.
【思考辨析】
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)=()n=a.( × )
(2)分数指数幂可以理解为个a相乘.( × )
(3)( × )
(4)函数y=a-x是R上的增函数.( × )
(5)函数(a>1)的值域是(0,+∞).( × )
(6)函数y=2x-1是指数函数.( × )
1.(教材改编)若函数f(x)=ax(a>0,且a≠1)的图象经过点P(2,),则f(-1)等于( )
A. B. C. D.4
答案 B
解析 由题意知=a2,所以a=,
所以f(x)=()x,所以f(-1)=()-1=.
2.(2017·青岛调研)已知函数f(x)=ax-2+2的图象恒过定点A,则A的坐标为( )
A.(0,1) B.(2,3)
C.(3,2) D.(2,2)
答案 B
解析 由a0=1知,当x-2=0,即x=2时,f(2)=3,即图象必过定点(2,3).
3.已知则a,b,c的大小关系是( )
A.cb>1,
又
∴cf(c)>f(b),则下列结论中,一定成立的是( )
A.a<0,b<0,c<0 B.a<0,b≥0,c>0
C.2-a<2c D.2a+2c<2
答案 (1)B (2)D
解析 (1)如图,观察易知,a,b的关系为af(c)>f(b),结合图象知,
00,
∴0<2a<1.
∴f(a)=|2a-1|=1-2a<1,
∴f(c)<1,∴0f(c),∴1-2a>2c-1,
∴2a+2c<2,故选D.
思维升华 (1)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些点,若不满足则排除.
(2)对于有关指数型函数的图象问题,一般是从最基本的指数函数的图象入手,通过平移、伸缩、对称变换而得到.特别地,当底数a与1的大小关系不确定时应注意分类讨论.
(3)有关指数方程、不等式问题的求解,往往利用相应的指数型函数图象,数形结合求解.
(1)函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.00 D.01.73 B.0.6-1>0.62
C.0.8-0.1>1.250.2 D.1.70.3<0.93.1
(2)设函数f(x)=若f(a)<1,则实数a的取值范围是________.
答案 (1)B (2)(-3,1)
解析 (1)选项B中,∵y=0.6x是减函数,
∴0.6-1>0.62.
(2)当a<0时,不等式f(a)<1可化为()a-7<1,
即()a<8,即()a<()-3,
∴a>-3.又a<0,∴-30,且a≠1)在区间[-1,1]上的最大值是14,则a的值为________.
答案 (1) (2)或3
解析 (1)令t=x,因为x∈[-3,2],
所以t∈,
故y=t2-t+1=2+.
当t=时,ymin=;当t=8时,ymax=57.
故所求函数的值域为.
(2)令ax=t,则y=a2x+2ax-1=t2+2t-1=(t+1)2-2.
当a>1时,因为x∈[-1,1],所以t∈[,a],又函数y=(t+1)2-2在上单调递增,
所以ymax=(a+1)2-2=14,解得a=3(负值舍去).
当0g(0)=0,所以函数g(x)的最小值是0.
2.指数函数底数的讨论
典例 (2016·日照模拟)已知函数(a,b为常数,且a>0,a≠1)在区间[-,0]上有最大值3,最小值, 则a,b的值分别为________.
错解展示
解析 令t=x2+2x=(x+1)2-1,
∵-≤x≤0,∴-1≤t≤0.
∵≤at≤1,∴b+≤b+at≤b+1,
由得
答案 2,2
现场纠错
解析 令t=x2+2x=(x+1)2-1,
∵x∈[-,0],∴t∈[-1,0].
①若a>1,函数f(x)=at在[-1,0]上为增函数,
∴at∈[,1],∈[b+,b+1],
依题意得解得
②若0b>c B.a>c>b
C.c>a>b D.b>c>a
答案 A
解析 由0.2<0.8,底数0.4<1知,y=0.4x在R上为减函数,所以0.40.2>0.40.8,即b>c.
又a=40.2>40=1,b=0.40.2<1,
所以a>b.综上,a>b>c.
4.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则f(x)的值域为( )
A.[9,81] B.[3,9]
C.[1,9] D.[1,+∞)
答案 C
解析 由f(x)过定点(2,1)可知b=2,
因为f(x)=3x-2在[2,4]上是增函数,
所以f(x)min=f(2)=1,f(x)max=f(4)=9.
故选C.
5.(2015·山东)若函数f(x)=是奇函数,则使f(x)>3成立的x的取值范围为( )
A.(-∞,-1) B.(-1,0)
C.(0,1) D.(1,+∞)
答案 C
解析 ∵f(x)为奇函数,∴f(-x)=-f(x),
即=-,整理得(a-1)(2x+1)=0,
∴a=1,∴f(x)>3即为>3,
当x>0时,2x-1>0,∴2x+1>3·2x-3,解得0-x-4,
即x2-3x-4<0,∴-10且a≠1)的图象有两个公共点,则a的取值范围是________.
答案 (0,)
解析 (数形结合法)
由图象可知0<2a<1,∴0,
不符合舍去;
②当<λ≤2时,g(t)min=g(λ)=-λ2+3,
令-λ2+3=1,得λ=(λ=-<,不符合舍去);
③当λ>2时,g(t)min=g(2)=-4λ+7,
令-4λ+7=1,得λ=<2,不符合舍去.
综上所述,实数λ的值为.