等差数列的前n项和教案5

等差数列的前n项和教案5

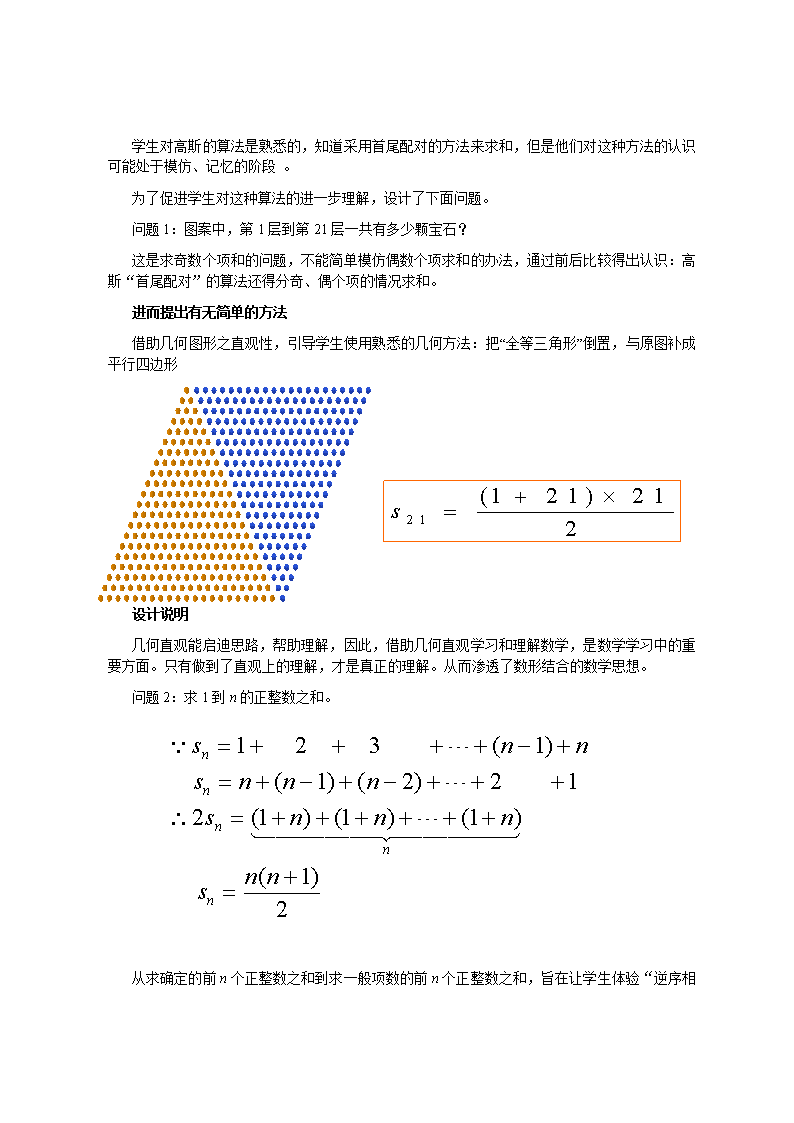
等差数列的前n项和 第一课时 一、教材分析 ‎1.教材地位与作用 本节课的教学内容是等差数列前n项和公式的推导及其简单应用。‎ 在推导等差数列前n项和公式的过程中，采用了：‎ ‎1．从特殊到一般的研究方法；‎ ‎2．等差数列的基本元表示 ；‎ ‎3．逆序相加求和。不仅得出了等差数列前n项和公式，而且对以后推导等比数列前n项和公式有一定的启发，也是一种常用的数学思想方法。‎ 等差数列前n项和是学习极限、微积分的基础，与数学课程的其它内容（函数、三角、不等式等）有着密切的联系。‎ ‎2.教学目标 知识与技能目标：‎ 掌握等差数列前n项和公式，能较熟练应用等差数列前n项和公式求和。‎ 过程与方法目标：‎ 经历公式的推导过程，体会数形结合的数学思想，体验从特殊到一般的研究方法，学会观察、归纳、反思。‎ 情感、态度与价值观目标：‎ 获得发现的成就感，逐步养成科学严谨的学习态度，提高代数推理的能力。‎ ‎3.教学重点、难点 ‎•等差数列前n项和公式是重点。‎ ‎•获得等差数列前n项和公式推导的思路是难点。‎ 二、教法分析 教学过程分为问题呈现阶段、探索与发现阶段、应用知识阶段。‎ 探索与发现公式推导的思路是教学的重点。如果直接介绍“逆序相加”求和，无疑就像波利亚所说的“帽子里跳出来的兔子”‎ ‎ ‎ ‎。所以在教学中采用以问题驱动、层层铺垫，从特殊到一般启发学生获得公式的推导方法。‎ 应用公式也是教学的重点。为了让学生较熟练掌握公式，可采用设计变式题的教学手段，通过“选择公式”，“变用公式”，“知三求二”三个层次来促进学生新的认知结构的形成 三、学法分析 建构主义学习理论认为，学习是学生积极主动的建构知识的过程，学习应该与学生熟悉的背景相联系。在教学中，让学生在问题情境中，经历知识的形成和发展，通过观察、操作、归纳、思考、探索、交流、反思参与学习，认识和理解数学知识，学会学习，发展能力。‎ 四、教学过程 ‎1．问题呈现 泰姬陵坐落于印度古都阿格，是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建，她宏伟壮观，纯白大理石砌建而成的主体建筑叫人心醉神迷，成为世界七大奇迹之一。陵寝以宝石镶饰，图案之细致令人叫绝。‎ 传说陵寝中有一个三角形图案，以相同大小的圆宝石镶饰而成，共有100层（见左图），奢靡之程度，可见一斑。‎ 你知道这个图案一共花了多少宝石吗？‎ 设计说明 ‎•源于历史，富有人文气息.‎ ‎•图中算数，激发学习兴趣.‎ ‎•承上启下，探讨高斯算法.‎ ‎2．2.探究发现 学生叙述高斯首尾配对的方法 ‎ ‎ 学生对高斯的算法是熟悉的，知道采用首尾配对的方法来求和，但是他们对这种方法的认识可能处于模仿、记忆的阶段 。‎ 为了促进学生对这种算法的进一步理解，设计了下面问题。‎ 问题1：图案中，第1层到第21层一共有多少颗宝石？‎ 这是求奇数个项和的问题，不能简单模仿偶数个项求和的办法，通过前后比较得出认识：高斯“首尾配对”的算法还得分奇、偶个项的情况求和。‎ 进而提出有无简单的方法 借助几何图形之直观性，引导学生使用熟悉的几何方法：把“全等三角形”倒置，与原图补成平行四边形 ‎：‎ 设计说明 几何直观能启迪思路，帮助理解，因此，借助几何直观学习和理解数学，是数学学习中的重要方面。只有做到了直观上的理解，才是真正的理解。从而渗透了数形结合的数学思想。‎ 问题2：求1到n的正整数之和。‎ 从求确定的前n个正整数之和到求一般项数的前n个正整数之和，旨在让学生体验“‎ ‎ ‎ 逆序相加求和”这一算法的合理性，从心理上完成对“首尾配对求和”算法的改进。‎ 问题3：如何求等差数列{an}前n项和sn?‎ 由于前面的铺垫，学生容易得出如下过程：‎ 图形直观 等差数列的性质(如果m+n=p+q那么am+an=ap+aq)‎ 设计说明 ‎（方法1） 许多的教学设计在介绍“等差数列前n项和”教学时，先复习或介绍等差数列的性质，然后在此基础上采用逆序相加推导公式。‎ ‎（方法2）《数学》第一册（上）（人民教育出版社）介绍的推导方法是先把等差数列用项（首项、尾项）、公差两个基本元表示，然后采用逆序相加推导公式。‎ 方法1是以学生掌握了等差数列的性质（教材内容始终未出现，增加了学生的负担）为基础的，起点比较高，因而方法 显得抽象一些，不容易被学生理解和信服。‎ 方法2的关键是等差数列的基本元表示——只要给定首项（尾项）和公差就可以确定该等差数列，反映了等差数列的本质，可以进一步促进学生对等差数列的理解。而且方法仅以等差数列的定义为基础，乃是学生熟悉的背景知识，因而显得比较直观，令人信服。‎ ‎3.公式应用 ‎（1）选用公式 例1某长跑运动员7天里每天的训练量（单位：m）是：‎ ‎1050000‎ ‎10000‎ ‎9500‎ ‎9000‎ ‎8500‎ ‎8000‎ ‎75000000‎ 这位长跑运动员7天共跑了多少米？‎ 本例提供了许多数据信息，学生可以从首项、尾项、项数出发，使用公式1，也可以从首项、公差、项数出发，使用公式2求和。‎ 通过两种方法的比较，引导学生应该根据信息选择适当的公式，以便于计算。‎ ‎（2）变用公式 例2等差数列－10，－6，－2，2，…的前多少项的和为54？‎ ‎ ‎ 本例已知首项，前n项和、并且可以求出公差，利用公式2求项数。‎ 事实上，在两个求和公式中各包含四个元素，从方程的角度，知三必能求余一。‎ ‎（3）知三求二 例3.在等差数列{an}中，已知d=20，n=37，sn=629，求a1和an。‎ 本例是使用等差数列的求和公式和通项公式求未知元。‎ 事实上，在求和公式、通项公式中共有首项、公差、项数、尾项、前n项和五个元素，如果已知其中三个，联列方程组，就可求其余二个。‎ 课堂小结 ‎•回顾从特殊到一般的研究方法；‎ ‎•体会等差数列的基本元表示方法，逆序相加的算法，及数形结合的数学思想；‎ ‎•掌握等差数列的两个求和公式及简单应用。‎ 作业布置 课本，练习1、2、3；习题3.3第2题（3、４）‎ ‎ ‎