【数学】2018届一轮复习北师大版三角函数的定义域和值域学案

【数学】2018届一轮复习北师大版三角函数的定义域和值域学案

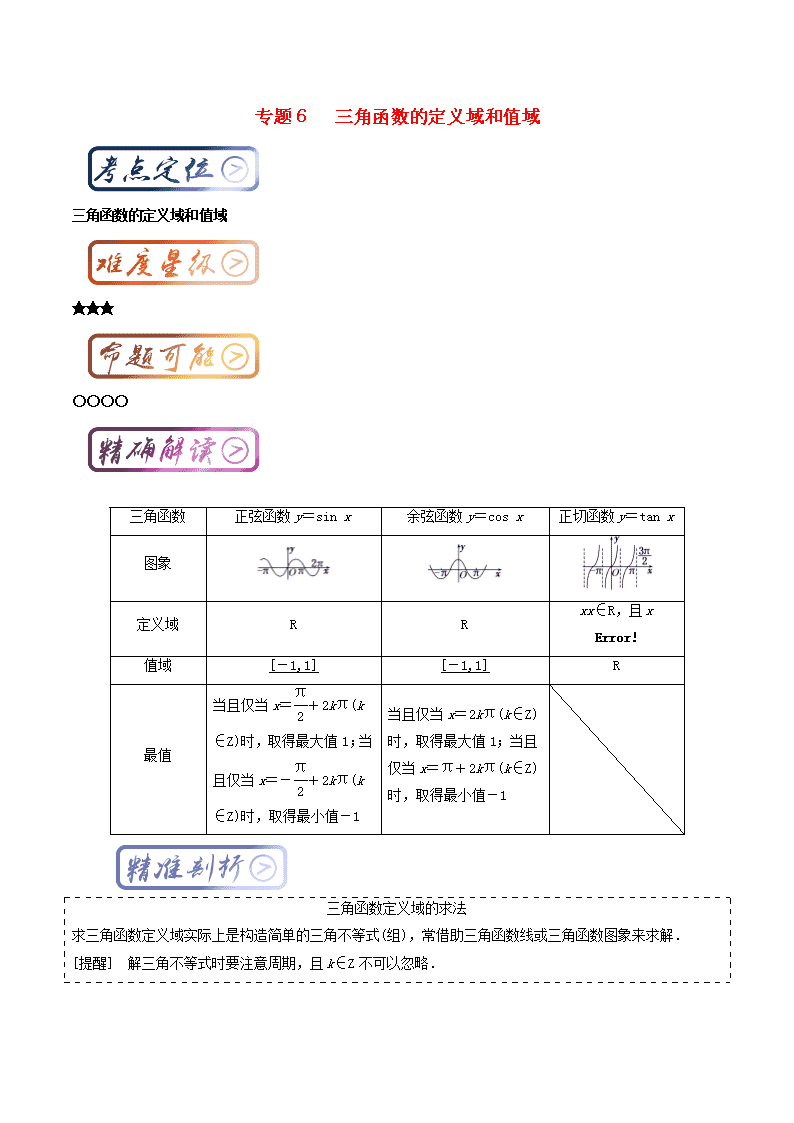
专题6 三角函数的定义域和值域 三角函数的定义域和值域 ‎★★★‎ ‎○○○○‎ 三角函数 正弦函数y＝sin x 余弦函数y＝cos x 正切函数y＝tan x 图象 定义域 R R xx∈R，且x 值域 ‎[－1,1]‎ ‎[－1,1]‎ R 最值 当且仅当x＝＋2kπ(k∈Z)时，取得最大值1；当且仅当x＝－＋2kπ(k∈Z)时，取得最小值－1‎ 当且仅当x＝2kπ(k∈Z)时，取得最大值1；当且仅当x＝π＋2kπ(k∈Z)时，取得最小值－1‎ 三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．‎ ‎[提醒]　解三角不等式时要注意周期，且k∈Z不可以忽略．　‎ ‎[例1]　函数y＝lg(2sin x－1)＋的定义域是________．‎ ‎1.　函数y＝2sin(0≤x≤9)的最大值与最小值之和为(　　)‎ A．2－ B．‎0 ‎‎ C．－1 D．－1－ ‎ [解析]　∵0≤x≤9，∴－≤x－≤，‎ ‎∴sin∈.‎ ‎∴y∈[－，2]，∴ymax＋ymin＝2－.‎ ‎(2)函数y＝3－sin x－2cos2x，x∈的值域为________．‎ ‎[解析]∵x∈，∴sin x∈.‎ 又y＝3－sin x－2cos2x＝3－sin x－2(1－sin2x)＝22＋，∴当sin x＝时，ymin＝；‎ 当sin x＝－或sin x＝1时，ymax＝2.‎ 故该函数的值域为.‎ ‎1.函数y＝ 的定义域为(　　)‎ A. B.(k∈Z)‎ C.(k∈Z)‎ D．R 解析：选C　要使函数有意义，则cos x－≥0，即cos x≥，解得2kπ－≤x≤2kπ＋，k∈Z.‎ ‎2.函数f(x)＝sin在区间上的最小值为(　　)‎ A．－1 B．－ C．0 D. 解析：选B　因为0≤x≤，所以－≤2x－≤，由正弦函数的图象知，－≤sin≤1，所以函数f(x)＝sin在区间上的最小值为－.‎ ‎3.函数y＝的定义域为________．‎ ‎4.函数y＝lg(sin 2x)＋的定义域为________．‎ 解析：由 得 ‎∴－3≤x<－或0

查看更多