高中数学人教a版选修1-2学业分层测评6分析法及其应用word版含解析
学业分层测评
(建议用时:45 分钟)
[学业达标]
一、选择题
1.若 a,b∈R,则 1
a3> 1
b3
成立的一个充分不必要条件是( )
A.ab>0 B.b>a
C.a
1
b3
,但 1
a3> 1
b3
不能推出 a 1
b3
的一个充分不必要条件.
【答案】 C
2.求证: 7-1> 11- 5.
证明:要证 7-1> 11- 5,
只需证 7+ 5> 11+1,
即证 7+2 7×5+5>11+2 11+1,即证 35> 11,
∵35>11,
∴原不等式成立.
以上证明应用了( )
A.分析法
B.综合法
C.分析法与综合法配合使用
D.间接证法
【解析】 该证明方法符合分析法的定义,故选 A.
【答案】 A
3.(2016·汕头高二检测)要证:a2+b2-1-a2b2≤0,只要证明( )
A.2ab-1-a2b2≤0
B.a2+b2-1-a4+b4
2
≤0
C.a+b2
2
-1-a2b2≤0
D.(a2-1)(b2-1)≥0
【解析】 要证 a2+b2-1-a2b2≤0,只要证明(a2-1)+b2(1-a2)≤0,只要
证明(a2-1)(1-b2)≤0,即证(a2-1)(b2-1)≥0.
【答案】 D
4.在不等边三角形中,a 为最大边,要想得到∠A 为钝角的结论,三边 a,
b,c 应满足什么条件( )
A.a2b2+c2 D.a2≤b2+c2
【解析】 由余弦定理得
cos A=b2+c2-a2
2bc <0,
∴b2+c2-a2<0,
即 b2+c2b>c,且 a+b+c=0,
求证: b2-ac< 3a”,索的因应是( )
A.a-b>0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
【解析】 由题意知 b2-ac< 3a⇐b2-ac<3a2
⇐b2+a(a+b)<3a2⇐b2+a2+ab<3a2
⇐b2+ab<2a2⇐2a2-ab-b2>0
⇐a2-ab+a2-b2>0⇐a(a-b)+(a+b)(a-b)>0
⇐a(a-b)-c(a-b)>0⇐(a-b)(a-c)>0,故选 C.
【答案】 C
二、填空题
6.(2016·烟台高二检测)设 A= 1
2a
+ 1
2b
,B= 2
a+b(a>0,b>0),则 A,B 的大
小关系为________.
【解析】 ∵A-B=a+b
2ab
- 2
a+b
=a+b2-4ab
2aba+b
= a-b2
2aba+b
≥0,∴A≥B.
【答案】 A≥B
7.(2016·西安高二检测)如果 a a>b b,则实数 a,b 应满足的条件是________.
【导学号:19220024】
【解析】 要使 a a>b b成立,只需(a a)2>(b b)2,只需 a3>b3>0,即 a,b
应满足 a>b>0.
【答案】 a>b>0
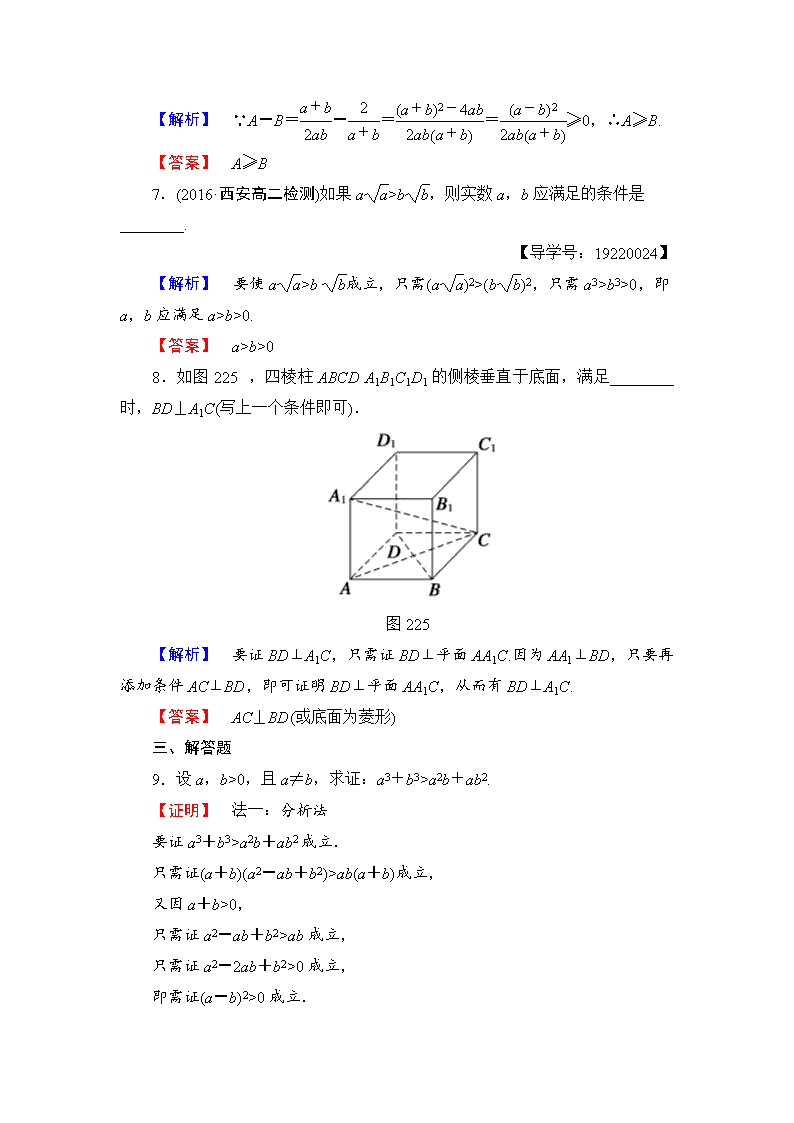
8.如图 225,四棱柱 ABCDA1B1C1D1 的侧棱垂直于底面,满足________
时,BD⊥A1C(写上一个条件即可).
图 225
【解析】 要证 BD⊥A1C,只需证 BD⊥平面 AA1C.因为 AA1⊥BD,只要再
添加条件 AC⊥BD,即可证明 BD⊥平面 AA1C,从而有 BD⊥A1C.
【答案】 AC⊥BD(或底面为菱形)
三、解答题
9.设 a,b>0,且 a≠b,求证:a3+b3>a2b+ab2.
【证明】 法一:分析法
要证 a3+b3>a2b+ab2 成立.
只需证(a+b)(a2-ab+b2)>ab(a+b)成立,
又因 a+b>0,
只需证 a2-ab+b2>ab 成立,
只需证 a2-2ab+b2>0 成立,
即需证(a-b)2>0 成立.
而依题设 a≠b,则(a-b)2>0 显然成立,
由此命题得证.
法二:综合法
a≠b⇒a-b≠0⇒(a-b)2>0⇒a2-2ab+b2>0⇒a2-ab+b2>ab.
注意到 a,b>0,a+b>0,由上式即得
(a+b)(a2-ab+b2)>ab(a+b).
∴a3+b3>a2b+ab2.
10.(2016·深圳高二检测)已知三角形的三边长为 a,b,c,其面积为 S,求
证:a2+b2+c2≥4 3S.
【证明】 要证 a2+b2+c2≥4 3S,
只要证 a2+b2+(a2+b2-2abcos C)≥2 3absin C,
即证 a2+b2≥2absin(C+30°),
因为 2absin(C+30°)≤2ab,
只需证 a2+b2≥2ab,
显然上式成立.所以 a2+b2+c2≥4 3S.
[能力提升]
1.已知 a,b,c,d 为正实数,且a
b a+b(a>0,b>0)
C. a- a-1< a-2- a-3(a≥3)
D. 2+ 10>2 6
【解析】 对于 A,∵a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,∴a2+b2
+c2≥ab+bc+ca;
对于 B,∵( a+ b)2=a+b+2 ab,( a+b)2=a+b,∴ a+ b> a+b;
对于 C,要证 a- a-1< a-2- a-3(a≥3)成立,只需证明 a+
a-3< a-2+ a-1,两边平方得 2a-3+2 aa-3<2a-3+2 a-2a-1,
即 aa-3< a-2a-1,两边平方得 a2-3a1+ p成立的正整数 p 的最大值是________.
【导学号:19220025】
【解析】 由 3+2 2>1+ p,得 p< 3+2 2-1,
即 p<( 3+2 2-1)2,
所以 p<12+4 6-4 2-2 3,
由于 12+4 6-4 2-2 3≈12.7,因此使不等式成立的正整数 p 的最大值是
12.
【答案】 12
4.(2016·唐山高二检测)已知 a,b,c 是不全相等的正数,且 0abc.
∵a,b,c 是不全相等的正数,
∴a+b
2
≥ ab>0,b+c
2
≥ bc>0,a+c
2
≥ ac>0,
∴a+b
2 ·b+c
2 ·a+c
2 > a2b2c2=abc.
即a+b
2 ·b+c
2 ·a+c
2 >abc 成立.
∴logx
a+b
2
+logx
b+c
2
+logx
a+c
2
查看更多