【数学】内蒙古乌兰察布市集宁一中西校区2019-2020学年高一下学期期中考试试题 （解析版）

【数学】内蒙古乌兰察布市集宁一中西校区2019-2020学年高一下学期期中考试试题 （解析版）

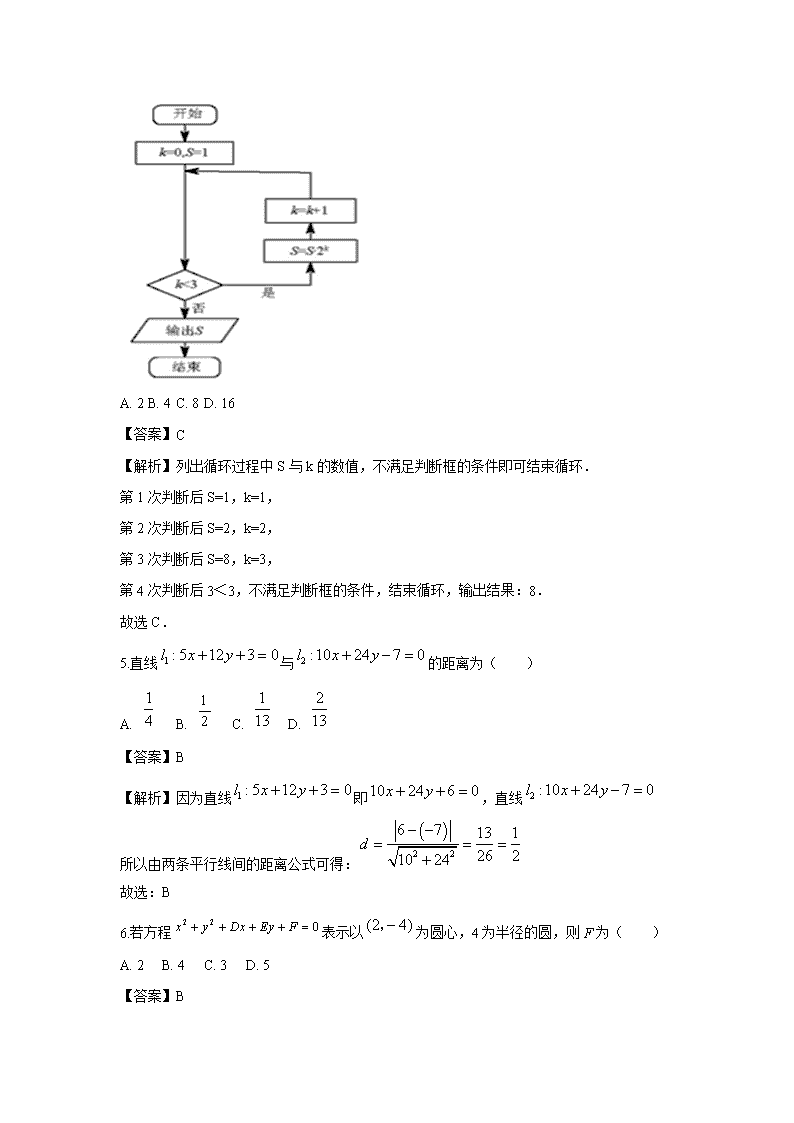
内蒙古乌兰察布市集宁一中西校区2019-2020学年高一下学期期中考试数学试题 一、选择题（每小题5分，共60分）‎ ‎1.过两点的直线的倾斜角为（ ）‎ A. 30° B. 60° C. 120° D. 150°‎ ‎【答案】A ‎【解析】直线AB的斜率,故直线AB的倾斜角，故选A.‎ ‎2.现有60瓶矿泉水，编号从1至60．若从中抽取6瓶检验，用系统抽样方法确定所抽编号为（ ）‎ A. 3，13，23，33，43，53 B. 2，14，26，38，42，56‎ C. 5，8，31，36，48，54 D. 5，10，15，20，25，30‎ ‎【答案】A ‎【解析】根据系统抽样原则，可知所抽取编号应成公差为的等差数列 B选项编号公差为；C选项编号不成等差；D选项编号公差为；可知错误 A选项编号满足公差为的等差数列，正确 本题正确选项：A ‎3.直线在两坐标轴上的截距之和为（ ）‎ A. 1 B. ‎-1 ‎C. 7 D. -7‎ ‎【答案】B ‎【解析】直线的横截距为，纵截距为 所以直线在两坐标轴上的截距之和为 故选：B ‎4.执行如图所示的程序框图，输出的S值为（ ）‎ A. 2 B. ‎4 ‎C. 8 D. 16‎ ‎【答案】C ‎【解析】列出循环过程中S与k的数值，不满足判断框的条件即可结束循环．‎ 第1次判断后S=1，k=1，‎ 第2次判断后S=2，k=2，‎ 第3次判断后S=8，k=3，‎ 第4次判断后3＜3，不满足判断框的条件，结束循环，输出结果：8．‎ 故选C．‎ ‎5.直线与的距离为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】因为直线即，直线 所以由两条平行线间的距离公式可得：‎ 故选：B ‎6.若方程表示以为圆心，4为半径的圆，则F为（ ）‎ A. 2 B. ‎4 ‎C. 3 D. 5‎ ‎【答案】B ‎【解析】因为方程表示以为圆心，4为半径的圆，‎ 所以，解得，所以F为4.故选：B ‎7.将一个总体分为A，B，C三层，其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本，则应从C层中抽取（ ）个个体.‎ A. 10 B. ‎20 ‎C. 30 D. 40‎ ‎【答案】B ‎【解析】由题,因为分层抽样,‎ 所以应从层中抽出,故选:B ‎8.对于下列表格所示五个散点，已知求得的线性回归方程为，则实数m的值为（ ）‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A 8 B. ‎8.2 ‎C. 8.3 D. 8.5‎ ‎【答案】A ‎【解析】由表可得 ‎ 因为线性回归方程经过样本中心点 ‎ 代入线性回归方程可得 解得 故选:A ‎9.若连续抛掷两次骰子得到的点数分别为m，n，则点P(m，n)在直线x＋y＝4上的概率是(　　)‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】利用分布计数原理求出所有的基本事件个数，在求出点落在直线x+y=4上包含的基本事件个数，利用古典概型的概率个数求出. 解：连续抛掷两次骰子出现的结果共有6×6=36，其中每个结果出现的机会都是等可能的，点P（m，n）在直线x+y=4上包含的结果有（1，3），（2，2），（3，1）共三个，所以点P（m，n）在直线x+y=4上的概率是3:36=1:12,故选D．‎ ‎10.从装有5个红球和3个白球的口袋内任取3个球，那么互斥而不对立的事件是（ ）‎ A. 至少有一个红球与都是红球 B. 至少有一个红球与都是白球 C. 恰有一个红球与恰有二个红球 D. 至少有一个红球与至少有一个白球 ‎【答案】C ‎【解析】从装有5个红球和3个白球的口袋内任取3个球，不同的取球情况共有以下几种：‎ ‎3个球全是红球；2个红球和1个白球；1个红球2个白球；3个全是白球.‎ 选项A中，事件“都是红球”是事件“至少有一个红球”的子事件；‎ 选项B中，事件“至少有一个红球”与事件“都是白球”是对立事件；‎ 选项D中，事件“至少有一个红球”与事件“至少有一个白球”的事件为“2个红球1个白球”与“1个红球2个白球”；‎ 选项C中，事件“恰有一个红球”与事件“恰有2个红球”互斥不对立，故选C.‎ ‎11.直线和的交点在y轴上，则k的值为（ ）‎ A. -24 B. ‎6 ‎C. D. -6‎ ‎【答案】C ‎【解析】因为两条直线和的交点在轴上，‎ 所以设交点为，‎ 所以，消去，可得．故选：C．‎ ‎【点睛】本题考查两条直线的交点坐标的求法与应用，考查计算能力，属于基础题．‎ ‎12.在两根相距6m的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于2m的概率（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】记“灯与两端距离都大于2”为事件A,则灯只能在中间2的绳子上挂，‎ 所以事件A发生的概率.‎ 二.填空题（每小题5分，共20分）‎ ‎13.若直线l过点，且与直线垂直，则直线l的方程为_________.‎ ‎【答案】‎ ‎【解析】由题意可设直线的方程为，‎ 把点代入可得，解得．‎ 直线的方程是．故答案为：．‎ ‎14.若圆C与圆(x＋2)2＋(y－1)2＝1关于原点对称，则圆C的方程是________‎ ‎【答案】‎ ‎【解析】已知圆圆心为，∴，∴圆方程为．‎ ‎15.圆与圆的公共弦的长为________．‎ ‎【答案】‎ ‎【解析】圆与圆相减得：‎ ‎，圆，所以圆心为，半径为，圆心到直线距离，‎ 所以公共弦长，故填：．‎ ‎16.已知一样本，，…，，其标准差，另一样本，，…，，其标准差_______.‎ ‎【答案】25.5‎ ‎【解析】一组数据，，，，的标准差，则方差，‎ 数据，，…，的方差为，则其标准差 故答案为：．‎ 三．计算题 ‎17.已知直线经过点，，直线经过点，.‎ ‎（1）若∥求a的值；‎ ‎（2）若，求a的值.‎ 解：（1）直线经过点，，‎ 的斜率为；‎ 直线经过点，，的斜率为，‎ 若，则，解得或；‎ ‎（2）若，当时，此时，，与题干不符；‎ 当时，的斜率存在，则，‎ 解得或．‎ 故当或时两直线垂直.‎ ‎18.从点作圆的切线l，求切线l的方程.‎ 解：由题意得切线方程斜率存在，所以可设方程为，即 或 切线的方程为或 ‎19.经过圆上任意一点P作y轴的垂线，垂足为Q，求线段的中点M的轨迹方程.‎ 解：设中点，则 在圆上，，‎ 即中点的轨迹方程为．‎ ‎20.从某居民区随机抽取个家庭，获得第个家庭的月收入 （单位：千元）与月储蓄 （单位：千元）‎ 的数据资料，算得，i，， .‎ ‎（1）求家庭的月储蓄对月收入的线性回归方程；‎ ‎（2）判断变量与之间是正相关还是负相关；‎ ‎（3）若该居民区某家庭月收入为千元，预测该家庭的月储蓄．‎ 附：‎ 解：‎ ‎(1)由题意知n＝10，，‎ 又，‎ ‎，‎ ‎∴，‎ ‎∴．‎ ‎∴所求线性回归方程为．‎ ‎(2)∵，‎ ‎∴变量y的值随x值的增加而增加，‎ ‎∴故x与y之间是正相关．‎ ‎(3)当x＝7时，（千元）‎ 故当该家庭的月收入为7千元时，可预测该家庭的月储蓄为千元．‎ ‎21.某商场举行购物抽奖促销活动，规定每位顾客从装有编号为0，1，2，3四个相同小球的抽奖箱中，每次取出一球，记下编号后放回，连续取两次，若取出的两个小球号码之和等于6，则中一等奖，等于5中二等奖，等于4或3中三等奖.‎ ‎（1）求中三等奖的概率；‎ ‎（2）求中奖的概率.‎ 解：（1）从装有编号为0，1，2，3四个相同小球的抽奖箱中，每次取出一球，记下编号后放回，连续取两次的基本事件总数为种，‎ 取出的两个小球号码之和等于4或3基本事件有：，共7种.‎ 所以中三等奖的概率；‎ ‎（2）取出的两个小球号码之和6基本事件有：，共1种.‎ 所以中一等奖的概率；‎ 取出的两个小球号码之和5基本事件有：，共2种.‎ 所以中二等奖的概率；‎ 所以中奖的概率 ‎22. 某中学高一女生共有450人，为了了解高一女生的身高情况，随机抽取部分高一女生测量身高，所得数据整理后列出频率分布表如下：‎ 组别 频数 频率 ‎145.5～149.5‎ ‎8‎ ‎0.16‎ ‎149.5～153.5‎ ‎6‎ ‎0.12‎ ‎153.5～157.5‎ ‎14‎ ‎0.28‎ ‎157.5～161.5‎ ‎10‎ ‎0.20‎ ‎161.5～165.5‎ ‎8‎ ‎0.16‎ ‎165.5～169.5‎ 合计 ‎（1）求出表中字母所对应的数值；‎ ‎（2）在给出的直角坐标系中画出频率分布直方图；‎ ‎（3）估计该校高一女生身高在149.5～165.5范围内有多少人？‎ 解： ‎ ‎（1）由题意落在区间内数据频数 频率为，总频率 ‎（2）频率分布直方图如下 ‎（3）该所学校高一女生身高在之间的比例为，则该校高一女生在此范围内的人数为（人）.‎