高考数学专题复习课件：2-2 函数的单调性与最值

高考数学专题复习课件：2-2 函数的单调性与最值

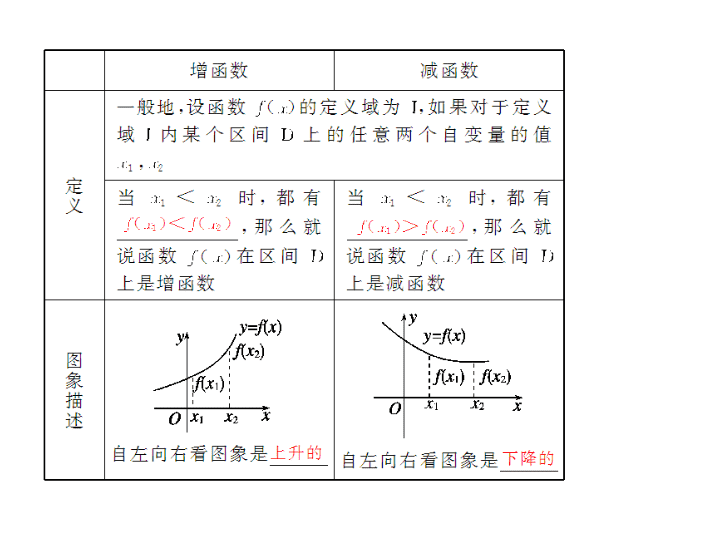
§ 2.2 　函数的单调性与最值 [ 考纲要求 ] 　 1. 理解函数的单调性、最大值、最小值及其几何意义 .2. 会利用函数的图象理解和研究函数的性质． 1 ． 函数的单调性 (1) 单调函数的定义 (2) 单调区间的定义 如果函数 y ＝ f ( x ) 在区间 D 上是 _______ 或 _______ ，那么就说函数 y ＝ f ( x ) 在这一区间具有 ( 严格的 ) 单调性， _______ 叫做 y ＝ f ( x ) 的单调区间． 增函数 减函数 区间 D 2 ． 函数的最值 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 在增函数与减函数的定义中，可以把 “ 任意两个自变量 ” 改为 “ 存在两个自变量 ” ． ( 　　 ) (2) 对于函数 f ( x ) ， x ∈ D ，若 x 1 ， x 2 ∈ D 且 ( x 1 － x 2 )·[ f ( x 1 ) － f ( x 2 )] ＞ 0 ，则函数 f ( x ) 在 D 上是增函数． ( 　　 ) 【 答案 】 (1) × 　 (2) √ 　 (3) × 　 (4) × 　 (5) × 　 (6) × 【 答案 】 D 2 ． (2017· 温州模拟 ) 若函数 f ( x ) ＝ |2 x ＋ a | 的单调递增区间是 [3 ，＋ ∞ ) ，则 a 的值为 ( 　　 ) A ．－ 2 B ． 2 C ．－ 6 D ． 6 【 答案 】 B 5 ． ( 教材改编 ) 已知函数 f ( x ) ＝ x 2 － 2 ax － 3 在区间 [1 ， 2] 上具有单调性，则实数 a 的取值范围为 ________________________________________________________________________ ． 【 解析 】 函数 f ( x ) ＝ x 2 － 2 ax － 3 的图象开口向上，对称轴为直线 x ＝ a ，画出草图如图所示． 由图象可知函数在 ( － ∞ ， a ] 和 [ a ，＋ ∞ ) 上都具有单调性，因此要使函数 f ( x ) 在区间 [1 ， 2] 上具有单调性，只需 a ≤ 1 或 a ≥ 2 ，从而 a ∈ ( － ∞ ， 1] ∪ [2 ，＋ ∞ ) ． 【 答案 】 ( － ∞ ， 1] ∪ [2 ，＋ ∞ ) 【 方法规律 】 确定函数单调性的方法： (1) 定义法和导数法，证明函数单调性只能用定义法和导数法； (2) 复合函数法，复合函数单调性的规律是 “ 同增异减 ” ； (3) 图象法，图象不连续的单调区间不能用 “ ∪ ” 连接． 【 答案 】 (1)2 　 (2) a ＜－ 1 【 方法规律 】 求函数最值的常用方法： (1) 单调性法：先确定函数的单调性，再由单调性求最值； (2) 图象法：先作出函数的图象，再观察其最高点、最低点，求出最值； (3) 换元法：对比较复杂的函数可通过换元转化为熟悉的函数，再用相应的方法求最值． 题型三　函数单调性的应用 命题点 1 　比较大小 【 例 3 】 (2016· 安徽皖北片第一次联考 ) 已知偶函数 f ( x ) 对于任意 x ∈ R 都有 f ( x ＋ 1) ＝－ f ( x ) ，且 f ( x ) 在区间 [0 ， 2] 上是递增的，则 f ( － 6.5) ， f ( － 1) ， f (0) 的大小关系是 ( 　　 ) A ． f (0) ＜ f ( － 6.5) ＜ f ( － 1) B ． f ( － 6.5) ＜ f (0) ＜ f ( － 1) C ． f ( － 1) ＜ f ( － 6.5) ＜ f (0) D ． f ( － 1) ＜ f (0) ＜ f ( － 6.5) 【 解析 】 由 f ( x ＋ 1) ＝－ f ( x ) ，得 f ( x ＋ 2) ＝－ f ( x ＋ 1) ＝ f ( x ) ， ∴ 函数 f ( x ) 的周期是 2. ∵ 函数 f ( x ) 为偶函数， ∴ f ( － 6.5) ＝ f ( － 0.5) ＝ f (0.5) ， f ( － 1) ＝ f (1) ． ∵ f ( x ) 在区间 [0 ， 2] 上是单调递增的， ∴ f (0) ＜ f (0.5) ＜ f (1) ，即 f (0) ＜ f ( － 6.5) ＜ f ( － 1) ． 【 答案 】 A 【 答案 】 A 【 方法规律 】 函数单调性应用问题的常见类型及解题策略 (1) 比较大小．比较函数值的大小，应将自变量转化到同一个单调区间内，然后利用函数的单调性解决． (2) 解不等式．在求解与抽象函数有关的不等式时，往往是利用函数的单调性将 “ f ” 符号脱掉，使其转化为具体的不等式求解．此时应特别注意函数的定义域． (3) 利用单调性求参数． ① 视参数为已知数，依据函数的图象或单调性定义，确定函数的单调区间，与已知单调区间比较求参数； ② 需注意若函数在区间 [ a ， b ] 上是单调的，则该函数在此区间的任意子集上也是单调的； ③ 分段函数的单调性，除注意各段的单调性外，还要注意衔接点的取值． 跟踪训练 3 (1) f ( x ) 是定义在 (0 ，＋ ∞ ) 上的单调增函数，满足 f ( xy ) ＝ f ( x ) ＋ f ( y ) ， f (3) ＝ 1 ，当 f ( x ) ＋ f ( x － 8) ≤ 2 时， x 的取值范围是 ( 　　 ) A ． (8 ，＋ ∞ ) B ． (8 ， 9] C ． [8 ， 9] D ． (0 ， 8) 【 答案 】 (1)B 　 (2)D 答题模板系列 1 确定抽象函数单调性解函数不等式 【 典例 】 ( 12 分 ) 函数 f ( x ) 对任意的 m 、 n ∈ R ，都有 f ( m ＋ n ) ＝ f ( m ) ＋ f ( n ) － 1 ，并且 x ＞ 0 时，恒有 f ( x ) ＞ 1. (1) 求证： f ( x ) 在 R 上是增函数； (2) 若 f (3) ＝ 4 ，解不等式 f ( a 2 ＋ a － 5) ＜ 2. 【 思维点拨 】 (1) 对于抽象函数的单调性的证明，只能用定义．应该构造出 f ( x 2 ) － f ( x 1 ) 并与 0 比较大小． (2) 将函数不等式中的抽象函数符号 “ f ” 运用单调性 “ 去掉 ” 是本题的切入点．要构造出 f ( M ) ＜ f ( N ) 的形式． 【 解析 】 (1) 证明 设 x 1 ， x 2 ∈ R ，且 x 1 ＜ x 2 ， ∴ x 2 － x 1 ＞ 0 ， ∵ 当 x ＞ 0 时， f ( x ) ＞ 1 ， ∴ f ( x 2 － x 1 ) ＞ 1.(2 分 ) f ( x 2 ) ＝ f [( x 2 － x 1 ) ＋ x 1 ] ＝ f ( x 2 － x 1 ) ＋ f ( x 1 ) － 1 ， (4 分 ) ∴ f ( x 2 ) － f ( x 1 ) ＝ f ( x 2 － x 1 ) － 1 ＞ 0 ⇒ f ( x 1 ) ＜ f ( x 2 ) ， ∴ f ( x ) 在 R 上为增函数． (6 分 ) (2) ∵ m ， n ∈ R ，不妨设 m ＝ n ＝ 1 ， ∴ f (1 ＋ 1) ＝ f (1) ＋ f (1) － 1 ⇒ f (2) ＝ 2 f (1) － 1 ， (8 分 ) f (3) ＝ 4 ⇒ f (2 ＋ 1) ＝ 4 ⇒ f (2) ＋ f (1) － 1 ＝ 4 ⇒ 3 f (1) － 2 ＝ 4 ， ∴ f (1) ＝ 2 ， ∴ f ( a 2 ＋ a － 5) ＜ 2 ＝ f (1) ， (10 分 ) ∵ f ( x ) 在 R 上为增函数， ∴ a 2 ＋ a － 5 ＜ 1 ⇒ － 3 ＜ a ＜ 2 ， 即 a ∈ ( － 3 ， 2) ． (12 分 ) 【 答题模板 】 解函数不等式问题的一般步骤： 第一步： ( 定性 ) 确定函数 f ( x ) 在给定区间上的单调性； 第二步： ( 转化 ) 将函数不等式转化为 f ( M ) ＜ f ( N ) 的形式； 第三步： ( 去 f ) 运用函数的单调性 “ 去掉 ” 函数的抽象符号 “ f ” ，转化成一般的不等式或不等式组； 第四步： ( 求解 ) 解不等式或不等式组确定解集； 第五步： ( 反思 ) 反思回顾．查看关键点，易错点及解题规范． 【 温馨提醒 】 本题对函数的单调性的判断是一个关键点．不会运用条件 x ＞ 0 时， f ( x ) ＞ 1 ，构造不出 f ( x 2 ) － f ( x 1 ) ＝ f ( x 2 － x 1 ) － 1 的形式，便找不到问题的突破口．第二个关键应该是将不等式化为 f ( M ) ＜ f ( N ) 的形式．解决此类问题的易错点：忽视了 M 、 N 的取值范围，即忽视了 f ( x ) 所在的单调区间的约束 . ► 方法与技巧 1 ．利用定义证明或判断函数单调性的步骤 (1) 取值； (2) 作差； (3) 定量； (4) 判断． 2 ．确定函数单调性有四种常用方法：定义法、导数法、复合函数法、图象法，也可利用单调函数的和差确定单调性． 3 ．求函数最值的常用求法：单调性法、图象法、换元法． ► 失误与防范 1 ．分段函数单调性不仅要考虑各段的单调性，还要注意衔接点． 2 ．函数在两个不同的区间上单调性相同，一般要分开写，用 “ ， ” 或 “ 和 ” 连接，不要用 “∪” .