2019年高考数学精讲二轮练习专题跟踪训练12
专题跟踪训练(十二)
一、选择题
1.(2018·福建福州八校联考)已知函数f(x)的导函数是f′(x),且满足f(x)=2xf′(1)+ln,则f(1)=( )
A.-e B.2 C.-2 D.e
[解析] 由已知得f′(x)=2f′(1)-,令x=1得f′(1)=2f′(1)-1,解得f′(1)=1,则f(1)=2f′(1)=2,故选B.
[答案] B
2.函数f(x)=x+的极值情况是( )
A.当x=1时,取极小值2,但无极大值
B.当x=-1时,取极大值-2,但无极小值
C.当x=-1时,取极小值-2;当x=1时,取极大值2
D.当x=-1时,取极大值-2;当x=1时,取极小值2
[解析] 求导得f′(x)=1-,令f′(x)=0,得x=±1,函数f(x)在区间(-∞,-1)和(1,+∞)上单调递增,在(-1,0)和(0,1)上单调递减,所以当x=-1时,取极大值-2,当x=1时,取极小值2,故选D.
[答案] D
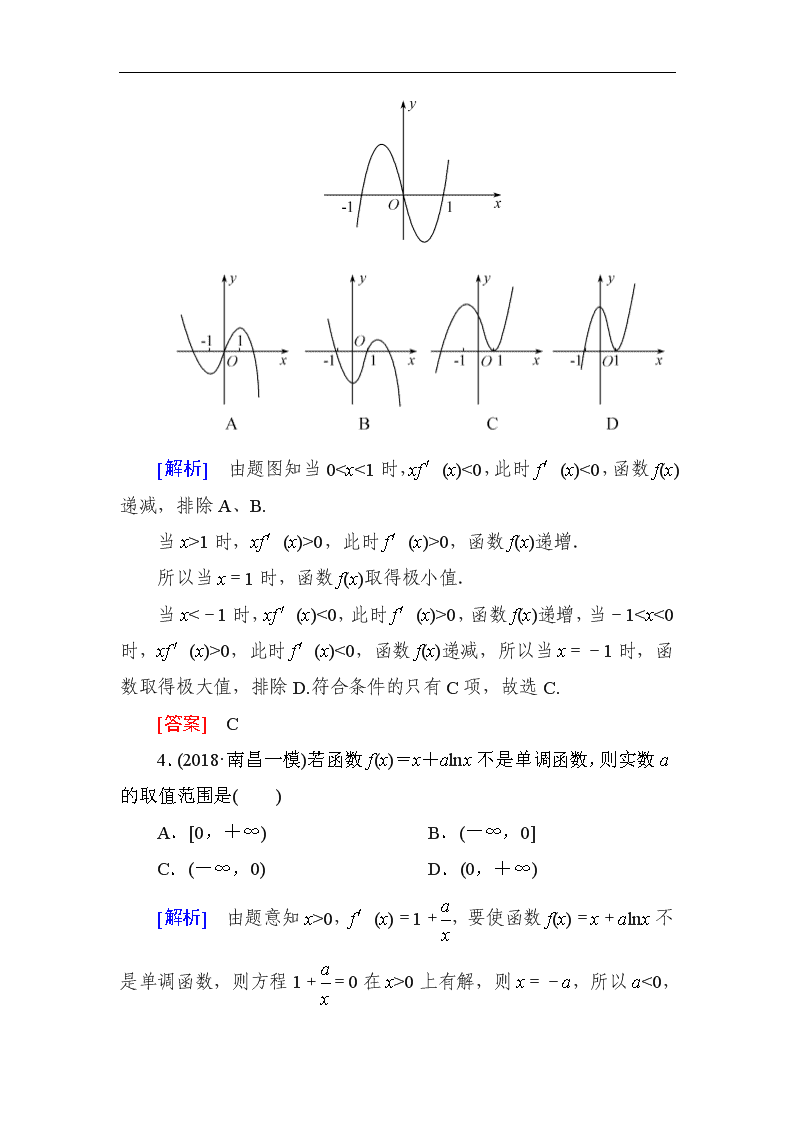
3.(2018·聊城模拟)已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则下面四个图象中,y=f(x)的图象大致是( )
[解析] 由题图知当0
1时,xf′(x)>0,此时f′(x)>0,函数f(x)递增.
所以当x=1时,函数f(x)取得极小值.
当x<-1时,xf′(x)<0,此时f′(x)>0,函数f(x)递增,当-10,此时f′(x)<0,函数f(x)递减,所以当x=-1时,函数取得极大值,排除D.符合条件的只有C项,故选C.
[答案] C
4.(2018·南昌一模)若函数f(x)=x+alnx不是单调函数,则实数a的取值范围是( )
A.[0,+∞) B.(-∞,0]
C.(-∞,0) D.(0,+∞)
[解析] 由题意知x>0,f′(x)=1+,要使函数f(x)=x+alnx不是单调函数,则方程1+=0在x>0上有解,则x=-a,所以a
<0,故选C.
[答案] C
5.(2018·海南八校联考)已知函数f(x)=3lnx-x2+x在区间(1,3)上有最大值,则实数a的取值范围是( )
A. B.
C. D.
[解析] 因为f′(x)=-2x+a-,所以结合题意可得f′(x)=-2x+a-在(1,3)上只有一个零点且单调递减,则问题转化为即解得-0)恒成立,则的最大值是( )
A.1 B.-1 C.e D.-e
[解析] 不等式lnx+1≥m-可化为lnx+1-m+≥0,令F(x)=lnx+1-m+(x>0),则F′(x)=-=,所以当x=n时,F(x)min=lnn+2-m,则lnn+2-m≥0⇒m≤2+lnn(n>0).所以≤.令G(n)=,则令G′(n)==0,可得n=,故G(n)max=
=e,即≤≤e,故选C.
[答案] C
二、填空题
7.(2018·武汉模拟)设曲线y=在点(3,2)处的切线与直线ax+y+1=0垂直,则a=________.
[解析] 因为y=,所以y′=-,则曲线y=在点(3,2)处的切线的斜率为y′=-.又因为切线与直线ax+y+1=0垂直,所以-·(-a)=-1,解得a=-2.
[答案] -2
8.(2018·南宁二模)曲线f(x)=xlnx在点(1,f(1))处的切线与两坐标轴围成的三角形的面积是________.
[解析] 因为f′(x)=1+lnx,且f(1)=0,f′(1)=1,所以切线l的斜率k=1,切线方程为y=x-1.令x=0,得y=-1,令y=0,得x=1,∴切线l与两坐标轴的交点坐标分别为A(0,-1),B(1,0),则|OA|=1,|OB|=1,∴S△ABO=×1×1=.
[答案]
9.(2018·河南安阳调研)已知函数f(x)=lnx+ax2-2x存在单调递减区间,则实数a的取值范围为________.
[解析] f′(x)=+ax-2=(x>0),函数f(x)存在单调递减区间,即定义域(0,+∞)内存在区间使ax2-2x+1≤0,等价于a小于在x∈(0,+∞)上的最大值,设g(x)=,则g′(x)=,可知,函数g(x)在区间(0,1)为增函数,在区间(1,+∞)为减函数,所以当x=1时,函数g(x)取得最大值,此时g(x)=1,所以a<1,故填(-∞,1).
[答案] (-∞,1)
三、解答题
10.(2018·贵阳模拟)已知函数f(x)=-lnx.
(1)求f(x)的单调区间;
(2)求函数f(x)在上的最大值和最小值(其中e是自然对数的底数).
[解] (1)f(x)=-lnx=1--lnx,
f(x)的定义域为(0,+∞).
∵f′(x)=-=,由f′(x)>0⇒01,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)由(1)得f(x)在上单调递增,在[1,e]上单调递减,
∴f(x)在上的最大值为f(1)=1--ln1=0.
又f=1-e-ln=2-e,f(e)=1--lne=-,且f0,即(-x2+2)ex>0,
因为ex>0,所以-x2+2>0,
解得-0,所以-x2+(a-2)x+a≥0,
则a≥==(x+1)-对x∈(-1,1)都成立.
令g(x)=(x+1)-,
则g′(x)=1+>0.
所以g(x)=(x+1)-在(-1,1)上单调递增.
所以g(x)0,所以x2-(a-2)x-a≥0对x∈R都成立.
所以Δ=(a-2)2+4a≤0,即a2+4≤0,这是不可能的.
故函数f(x)不可能在R上单调递减.
12.(2018·辽宁五校模拟)已知函数f(x)=2lnx+x2-2ax(a>0).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1,x2(x12时,Δ>0,方程x2-ax+1=0有两个不同的实根,分别设为x3,x4,不妨令x30,当x∈(x3,x4)时,
f′(x)<0,当x∈(x4,+∞)时,f′(x)>0,
所以函数f(x)在上单调递增,在上单调递减,在上单调递增.
综上:当02时,f(x)在上单调递增,在上单调递减,在上单调递增.
(2)由(1)得f(x)在(x1,x2)上单调递减,x1+x2=a,x1·x2=1,
则f(x1)-f(x2)=2ln+(x1-x2)(x1+x2-2a)=2ln+=2ln+-,
令t=,则0
查看更多