高中数学第8章圆锥曲线方程(第13课时)抛物线及其标准方程(1)
课 题:8.5抛物线及其标准方程(一)
教学目的:
1.使学生掌握抛物线的定义,标准方程及其推导过程;
2.根据定义画出抛物线的草图
3.使学生能熟练地运用坐标,进一步提高学生“应用数学”的水平
教学重点:抛物线的定义
教学难点:抛物线标准方程的不同形式
授课类型:新授课
课时安排:1课时
教 具:多媒体、实物投影仪
内容分析:
“抛物线及其标准方程”是教材第八章第五节的内容,也是本章介绍的最后一种圆锥知识 学好本节对于完整地掌握二次曲线,有着不可替代的作用 作为教学大纲规定的重点内容,高考必考的考点,这节教材继续着力于教会学生运用坐标法解题以及培养学生的对立统一的思想观点
本节教材与前面的内容和结构都有相似之处 但抛物线的确定过程中只有一个定点,所以这里要从对值的讨论来导入新课
教材利用教具演示引出抛物线定义,这种直观形象的过程类似于椭圆、双曲线定义引出过程,同学们已有一定的经验 但这三者毕竟有着各自的特征,尤其是抛物线形成中依赖于一点一线而非两点,所以演示操作时除了讲出教材上的话之外还要适当与前面的椭圆、双曲线相关内容进行对比说明
像椭圆和双曲线一样,抛物线的标准方程不只一种形式,而是共有4种形式之多 为此应注意两点:一是要对四种方程形式进行列表对比,对其中的图形特征(如开口方向、顶点、对称轴等)也须作特别说明;二是要指出不能把抛物线当成双曲线的一支 当抛物线上的点趋向于无穷远时,抛物线没有渐近线;而双曲线上的点趋于无穷远时,它有渐近线
本节内容分为两课时 第一课时主要内容为抛物线的定义、标准方程及其推导、课本中的例一 第二课时的主要内容是课本中的例二、例三
教学过程:
一、复习引入:
1 椭圆的第二定义:一动点到定点的距离和它到一条定直线的距离的比是一个内的常数,那么这个点的轨迹叫做椭圆 其中定点叫做焦点,定直线叫做准线,常数就是离心率
2. 双曲线的第二定义:一动点到定点F的距离与到一条定直线的距离之比是一个内的常数,那么这个点的轨迹叫做双曲线 其中定点叫做双曲线的焦点,定直线叫做双曲线的准线 常数e是双曲线的离心率
3.问题:到定点距离与到定直线距离之比是定值e的点的轨迹,当0
1时是双曲线。此时自然想到,当e=1时轨迹是什么?
若一动点到定点F的距离与到一条定直线的距离之比是一个常数时,那么这个点的轨迹是什么曲线?
把一根直尺固定在图板上直线L位置,把一块三角板的一条直角边紧靠着真心直尺的边缘,再把一条细绳的一端固定在三角板的另一条直角边的一点A,取绳长等于点A到直角标顶点C的长(即点A到直线L的距离),并且把绳子的另一端固定在图板上的一点F 用铅笔尖扣着绳子,使点A到笔尖的一段绳子紧靠着三角板,然后将三角板沿着直尺上下滑动,笔尖就在图板上描出了一条曲线
二、讲解新课:
1. 抛物线定义:
平面内与一个定点F和一条定直线的距离相等的点的轨迹叫做抛物线 定点F叫做抛物线的焦点,定直线叫做抛物线的准线
2.推导抛物线的标准方程:
如图所示,建立直角坐标系系,设|KF|=(>0),那么焦点F的坐标为,准线的方程为,
设抛物线上的点M(x,y),则有
化简方程得
方程叫做抛物线的标准方程
(1)它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是F(,0),它的准线方程是
(2)一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式:,,.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下
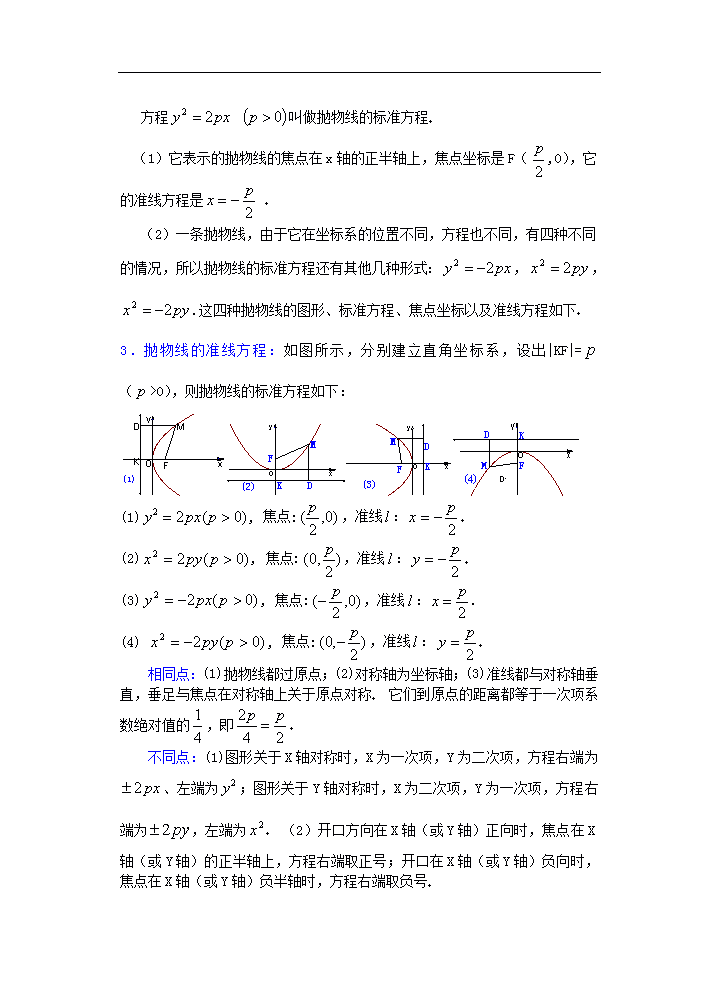
3.抛物线的准线方程:如图所示,分别建立直角坐标系,设出|KF|=(>0),则抛物线的标准方程如下:
(1), 焦点:,准线:
(2), 焦点:,准线:
(3), 焦点:,准线:
(4) , 焦点:,准线:
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的,即
不同点:(1)图形关于X轴对称时,X为一次项,Y为二次项,方程右端为、左端为;图形关于Y轴对称时,X为二次项,Y为一次项,方程右端为,左端为 (2)开口方向在X轴(或Y轴)正向时,焦点在X轴(或Y轴)的正半轴上,方程右端取正号;开口在X轴(或Y轴)负向时,焦点在X轴(或Y轴)负半轴时,方程右端取负号
点评:
(1)建立坐标系是坐标法的思想基础,但不同的建立方式使所得的方程繁简不同,布置学生自己写出推导过程并与课文对照可以培养学生动手能力、自学能力,提高教学效果 ,进一步明确抛物线上的点的几何意义
(2)猜想是数学问题解决中的一类重要方法,请同学们根据推导出的(1)的标准方程猜想其它几个结论,非常有利于培养学生归纳推理或类比推理的能力,帮助他们形成良好的直觉思维—数学思维的一种基本形式 另外让学生推导和猜想出抛物线标准方程所有的四种形式,也比老师直接写出这些方程给学生带来的理解和记忆的效果更好
(3)对四种抛物线的图形、标准方程、焦点坐标以及准线方程进行完整的归纳小结,让学生通过对比分析全面深刻地理解和掌握它们
三、讲解范例:
例1 (1)已知抛物线标准方程是,求它的焦点坐标和准线方程
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程
分析:(1)在标准方程下焦点坐标和准线方程都是用p的代数式表示的,所以只要求出p即可;
(2)求的是标准方程,因此所指抛物线应过原点,结合焦点坐标求出p,问题易解。
解析:(1)p=3,焦点坐标是(,0)准线方程是x=-.
(2)焦点在y轴负半轴上,=2,
所以所求抛物线的标准议程是.
例2 已知抛物线的标准方程是(1)y2=12x,(2)y=12x2,求它的焦点坐标和准线方程.
分析:这是关于抛物线标准方程的基本例题,关键是(1)根据示意图确定属于哪类标准形式,(2)求出参数p的值.
解:(1)p=6,焦点坐标是(3,0)准线方程是x=-3.
(2)先化为标准方程,,焦点坐标是(0,),
准线方程是y=-.
例3 求满足下列条件的抛物线的标准方程:
(1)焦点坐标是F(-5,0)
(2)经过点A(2,-3)
分析:抛物线的标准方程中只有一个参数p,因此,只要确定了抛物线属于哪类标准形式,再求出p值就可以写出其方程,但要注意两解的情况(如第(2)小题).
解:(1)焦点在x轴负半轴上,=5,
所以所求抛物线的标准议程是.
(2)经过点A(2,-3)的抛物线可能有两种标准形式:
y2=2px或x2=-2py.
点A(2,-3)坐标代入,即9=4p,得2p=
点A(2,-3)坐标代入x2=-2py,即4=6p,得2p=
∴所求抛物线的标准方程是y2=x或x2=-y
四、课堂练习:
1.求下列抛物线的焦点坐标和准线方程
(1)y2=8x (2)x2=4y (3)2y2+3x=0 (4)
2.根据下列条件写出抛物线的标准方程
(1)焦点是F(-2,0)
(2)准线方程是
(3)焦点到准线的距离是4,焦点在y轴上
(4)经过点A(6,-2)
3.抛物线x2=4y上的点p到焦点的距离是10,求p点坐标
课堂练习答案:
1.(1)F(2,0),x=-2 (2)(0,1),y=-1
(3)(,0),x= (4)(0,),y=
2.(1)y2=-8x (2)x2=-y (3)x2=8y或x2=-8y
(4) 或
3.(±6,9)
点评:练习时注意(1)由焦点位置或准线方程正确判断抛物线标准方程的类型;(2)p表示焦点到准线的距离故p>0;(3)根据图形判断解有几种可能
五、小结 :小结抛物线的定义、焦点、准线及其方程的概念;
六、课后作业:
七、板书设计(略)
八、课后记: