2015年全国统一高考数学试卷（文科）（新课标ⅱ）

2015年全国统一高考数学试卷（文科）（新课标ⅱ）

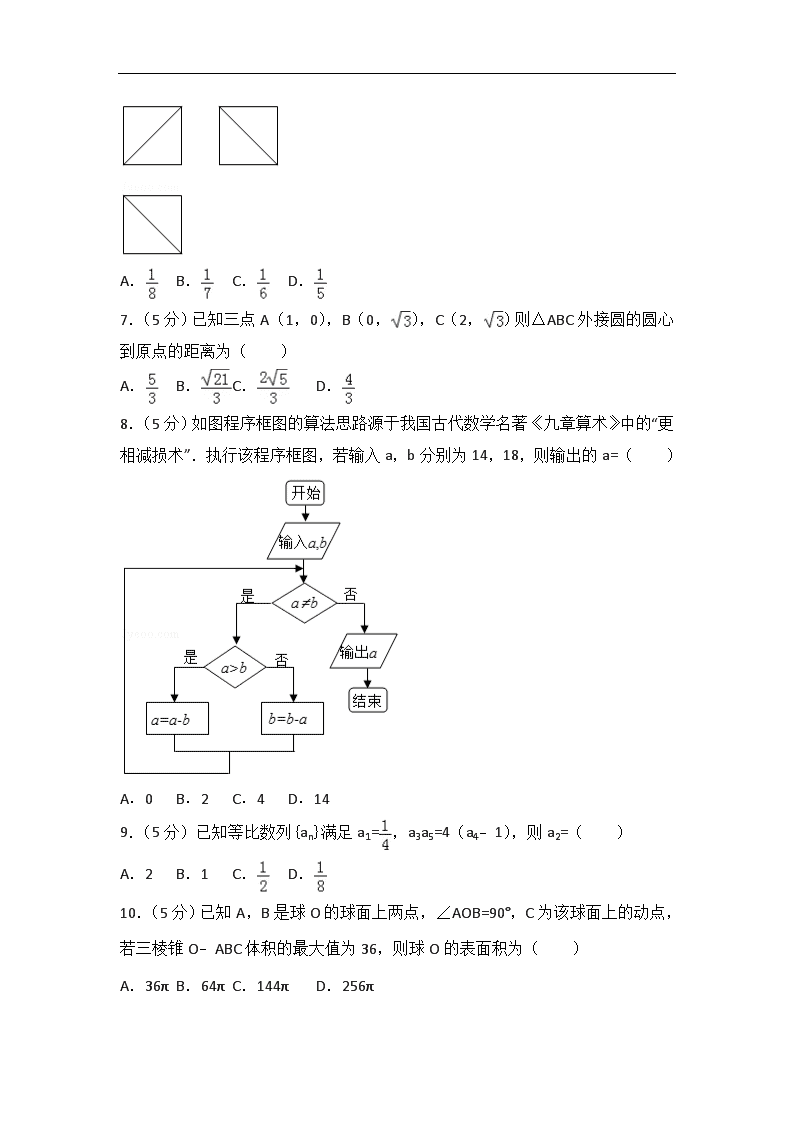
‎2015年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分 ‎1．（5分）已知集合A={x|﹣1＜x＜2}，B={x|0＜x＜3}，则A∪B=（　　）‎ A．（﹣1，3） B．（﹣1，0） C．（0，2） D．（2，3）‎ ‎2．（5分）若为a实数，且=3+i，则a=（　　）‎ A．﹣4 B．﹣3 C．3 D．4‎ ‎3．（5分）根据如图给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（　　）‎ A．逐年比较，2008年减少二氧化硫排放量的效果最显著 B．2007年我国治理二氧化硫排放显现成效 C．2006年以来我国二氧化硫年排放量呈减少趋势 D．2006年以来我国二氧化硫年排放量与年份正相关 ‎4．（5分）=（1，﹣1），=（﹣1，2）则（2+）=（　　）‎ A．﹣1 B．0 C．1 D．2‎ ‎5．（5分）已知Sn是等差数列{an}的前n项和，若a1+a3+a5=3，则S5=（　　）‎ A．5 B．7 C．9 D．11‎ ‎6．（5分）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（　　）‎ A． B． C． D．‎ ‎7．（5分）已知三点A（1，0），B（0，），C（2，）则△ABC外接圆的圆心到原点的距离为（　　）‎ A． B． C． D．‎ ‎8．（5分）如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（　　）‎ A．0 B．2 C．4 D．14‎ ‎9．（5分）已知等比数列{an}满足a1=，a3a5=4（a4﹣1），则a2=（　　）‎ A．2 B．1 C． D．‎ ‎10．（5分）已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（　　）‎ A．36π B．64π C．144π D．256π ‎11．（5分）如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP=x．将动点P到A，B两点距离之和表示为x的函数f（x），则y=f（x）的图象大致为（　　）‎ A． B． C． D．‎ ‎12．（5分）设函数f（x）=ln（1+|x|）﹣，则使得f（x）＞f（2x﹣1）成立的x的取值范围是（　　）‎ A．（﹣∞，）∪（1，+∞） B．（，1）‎ C．（） D．（﹣∞，﹣，）‎ ‎　‎ 二、填空题 ‎13．（3分）已知函数f（x）=ax3﹣2x的图象过点（﹣1，4）则a=　 　．‎ ‎14．（3分）若x，y满足约束条件，则z=2x+y的最大值为　 　．‎ ‎15．（3分）已知双曲线过点且渐近线方程为y=±x，则该双曲线的标准方程是　 　．‎ ‎16．（3分）已知曲线y=x+lnx在点（1，1）处的切线与曲线y=ax2+（a+2）x+1相切，则a=　 　．‎ ‎　‎ 三．解答题 ‎17．△ABC中，D是BC上的点，AD平分∠BAC，BD=2DC ‎（Ⅰ） 求．‎ ‎（Ⅱ） 若∠BAC=60°，求∠B．‎ ‎18．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表 B地区用户满意度评分的频数分布表 满意度评分分组 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ ‎[90，100）‎ 频数 ‎2‎ ‎8‎ ‎14‎ ‎10‎ ‎6‎ ‎（1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）‎ ‎（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：‎ 满意度评分 低于70分 ‎70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 估计哪个地区用户的满意度等级为不满意的概率大？说明理由．‎ ‎19．（12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形 ‎（Ⅰ）在图中画出这个正方形（不必说出画法和理由）‎ ‎（Ⅱ）求平面α把该长方体分成的两部分体积的比值．‎ ‎20．椭圆C：=1，（a＞b＞0）的离心率，点（2，）在C上．‎ ‎（1）求椭圆C的方程；‎ ‎（2）直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值．‎ ‎21．设函数f（x）=lnx+a（1﹣x）．‎ ‎（Ⅰ）讨论：f（x）的单调性；‎ ‎（Ⅱ）当f（x）有最大值，且最大值大于2a﹣2时，求a的取值范围．‎ ‎　‎ 四、选修4-1：几何证明选讲 ‎22．（10分）如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．‎ ‎（1）证明：EF∥BC；‎ ‎（2）若AG等于⊙O的半径，且AE=MN=2，求四边形EBCF的面积．‎ ‎　‎ 五、选修4-4：坐标系与参数方程 ‎23．（10分）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2‎ ‎：ρ=2sinθ，C3：ρ=2cosθ．‎ ‎（1）求C2与C3交点的直角坐标；‎ ‎（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．‎ ‎　‎ 六、选修4-5不等式选讲 ‎24．（10分）设a，b，c，d均为正数，且a+b=c+d，证明：‎ ‎（1）若ab＞cd，则+＞+；‎ ‎（2）+＞+是|a﹣b|＜|c﹣d|的充要条件．‎ ‎　‎ ‎2015年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分 ‎1．（5分）已知集合A={x|﹣1＜x＜2}，B={x|0＜x＜3}，则A∪B=（　　）‎ A．（﹣1，3） B．（﹣1，0） C．（0，2） D．（2，3）‎ ‎【分析】根据集合的基本运算进行求解即可．‎ ‎【解答】解：∵A={x|﹣1＜x＜2}，B={x|0＜x＜3}，‎ ‎∴A∪B={x|﹣1＜x＜3}，‎ 故选：A．‎ ‎【点评】本题主要考查集合的基本运算，比较基础．‎ ‎　‎ ‎2．（5分）若为a实数，且=3+i，则a=（　　）‎ A．﹣4 B．﹣3 C．3 D．4‎ ‎【分析】根据复数相等的条件进行求解即可．‎ ‎【解答】解：由，得2+ai=（1+i）（3+i）=2+4i，‎ 则a=4，‎ 故选：D．‎ ‎【点评】本题主要考查复数相等的应用，比较基础．‎ ‎　‎ ‎3．（5分）根据如图给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是（　　）‎ A．逐年比较，2008年减少二氧化硫排放量的效果最显著 B．2007年我国治理二氧化硫排放显现成效 C．2006年以来我国二氧化硫年排放量呈减少趋势 D．2006年以来我国二氧化硫年排放量与年份正相关 ‎【分析】A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多，故A正确；‎ B从2007年开始二氧化硫排放量变少，故B正确；‎ C从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C正确；‎ D2006年以来我国二氧化硫年排放量越来越少，与年份负相关，故D错误．‎ ‎【解答】解：A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少，且减少的最多，故A正确；‎ B2004﹣2006年二氧化硫排放量越来越多，从2007年开始二氧化硫排放量变少，故B正确；‎ C从图中看出，2006年以来我国二氧化硫年排放量越来越少，故C正确；‎ D2006年以来我国二氧化硫年排放量越来越少，而不是与年份正相关，故D错误．‎ 故选：D．‎ ‎【点评】本题考查了学生识图的能力，能够从图中提取出所需要的信息，属于基础题．‎ ‎　‎ ‎4．（5分）=（1，﹣1），=（﹣1，2）则（2+）=（　　）‎ A．﹣1 B．0 C．1 D．2‎ ‎【分析】利用向量的加法和数量积的坐标运算解答本题．‎ ‎【解答】解：因为=（1，﹣1），=（﹣1，2）则（2+）=（1，0）•（1，﹣1）=1；‎ 故选：C．‎ ‎【点评】本题考查了向量的加法和数量积的坐标运算；属于基础题目．‎ ‎　‎ ‎5．（5分）已知Sn是等差数列{an}的前n项和，若a1+a3+a5=3，则S5=（　　）‎ A．5 B．7 C．9 D．11‎ ‎【分析】由等差数列{an}的性质，a1+a3+a5=3=3a3，解得a3．再利用等差数列的前n项和公式即可得出．‎ ‎【解答】解：由等差数列{an}的性质，a1+a3+a5=3=3a3，解得a3=1．‎ 则S5==5a3=5．‎ 故选：A．‎ ‎【点评】本题考查了等差数列的通项公式及其性质、前n项和公式，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎6．（5分）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（　　）‎ A． B． C． D．‎ ‎【分析】由三视图判断，正方体被切掉的部分为三棱锥，把相关数据代入棱锥的体积公式计算即可．‎ ‎【解答】解：设正方体的棱长为1，由三视图判断，正方体被切掉的部分为三棱锥，‎ ‎∴正方体切掉部分的体积为×1×1×1=，‎ ‎∴剩余部分体积为1﹣=，‎ ‎∴截去部分体积与剩余部分体积的比值为．‎ 故选：D．‎ ‎【点评】本题考查了由三视图判断几何体的形状，求几何体的体积．‎ ‎　‎ ‎7．（5分）已知三点A（1，0），B（0，），C（2，）则△ABC外接圆的圆心到原点的距离为（　　）‎ A． B． C． D．‎ ‎【分析】利用外接圆的性质，求出圆心坐标，再根据圆心到原点的距离公式即可求出结论．‎ ‎【解答】解：因为△ABC外接圆的圆心在直线BC垂直平分线上，即直线x=1上，‎ 可设圆心P（1，p），由PA=PB得 ‎|p|=，‎ 得p=‎ 圆心坐标为P（1，），‎ 所以圆心到原点的距离|OP|===，‎ 故选：B．‎ ‎【点评】本题主要考查圆性质及△ABC外接圆的性质，了解性质并灵运用是解决本题的关键．‎ ‎　‎ ‎8．（5分）如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（　　）‎ A．0 B．2 C．4 D．14‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的a，b的值，当a=b=2时不满足条件a≠b，输出a的值为2．‎ ‎【解答】解：模拟执行程序框图，可得 a=14，b=18‎ 满足条件a≠b，不满足条件a＞b，b=4‎ 满足条件a≠b，满足条件a＞b，a=10‎ 满足条件a≠b，满足条件a＞b，a=6‎ 满足条件a≠b，满足条件a＞b，a=2‎ 满足条件a≠b，不满足条件a＞b，b=2‎ 不满足条件a≠b，输出a的值为2．‎ 故选：B．‎ ‎【点评】本题主要考查了循环结构程序框图，属于基础题．‎ ‎　‎ ‎9．（5分）已知等比数列{an}满足a1=，a3a5=4（a4﹣1），则a2=（　　）‎ A．2 B．1 C． D．‎ ‎【分析】利用等比数列的通项公式即可得出．‎ ‎【解答】解：设等比数列{an}的公比为q，‎ ‎∵，a3a5=4（a4﹣1），‎ ‎∴=4，‎ 化为q3=8，解得q=2‎ 则a2==．‎ 故选：C．‎ ‎【点评】本题考查了等比数列的通项公式，属于基础题．‎ ‎　‎ ‎10．（5分）已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（　　）‎ A．36π B．64π C．144π D．256π ‎【分析】当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，利用三棱锥O﹣ABC体积的最大值为36，求出半径，即可求出球O的表面积．‎ ‎【解答】解：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，设球O的半径为R，此时VO﹣ABC=VC﹣AOB===36，故R=6，则球O的表面积为4πR2=144π，‎ 故选：C．‎ ‎【点评】本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大是关键．‎ ‎　‎ ‎11．（5分）如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP=x．将动点P到A，B两点距离之和表示为x的函数f（x），则y=f（x）的图象大致为（　　）‎ A． B． C． D．‎ ‎【分析】根据函数图象关系，利用排除法进行求解即可．‎ ‎【解答】解：当0≤x≤时，BP=tanx，AP==，‎ 此时f（x）=+tanx，0≤x≤，此时单调递增，‎ 当P在CD边上运动时，≤x≤且x≠时，‎ 如图所示，tan∠POB=tan（π﹣∠POQ）=tanx=﹣tan∠POQ=﹣=﹣，‎ ‎∴OQ=﹣，‎ ‎∴PD=AO﹣OQ=1+，PC=BO+OQ=1﹣，‎ ‎∴PA+PB=，‎ 当x=时，PA+PB=2，‎ 当P在AD边上运动时，≤x≤π，PA+PB=﹣tanx，‎ 由对称性可知函数f（x）关于x=对称，‎ 且f（）＞f（），且轨迹为非线型，‎ 排除A，C，D，‎ 故选：B．‎ ‎【点评】本题主要考查函数图象的识别和判断，根据条件先求出0≤x≤时的解析式是解决本题的关键．‎ ‎　‎ ‎12．（5分）设函数f（x）=ln（1+|x|）﹣，则使得f（x）＞f（2x﹣1）成立的x的取值范围是（　　）‎ A．（﹣∞，）∪（1，+∞） B．（，1）‎ C．（） D．（﹣∞，﹣，）‎ ‎【分析】根据函数的奇偶性和单调性之间的关系，将不等式进行转化即可得到结论．‎ ‎【解答】解：∵函数f（x）=ln（1+|x|）﹣为偶函数，‎ 且在x≥0时，f（x）=ln（1+x）﹣，‎ 导数为f′（x）=+＞0，‎ 即有函数f（x）在[0，+∞）单调递增，‎ ‎∴f（x）＞f（2x﹣1）等价为f（|x|）＞f（|2x﹣1|），‎ 即|x|＞|2x﹣1|，‎ 平方得3x2﹣4x+1＜0，‎ 解得：＜x＜1，‎ 所求x的取值范围是（，1）．‎ 故选：B．‎ ‎【点评】本题主要考查函数奇偶性和单调性的应用，综合考查函数性质的综合应用，运用偶函数的性质是解题的关键．‎ ‎　‎ 二、填空题 ‎13．（3分）已知函数f（x）=ax3﹣2x的图象过点（﹣1，4）则a=　﹣2　．‎ ‎【分析】f（x）是图象过点（﹣1，4），从而该点坐标满足函数f（x）解析式，从而将点（﹣1，4）带入函数f（x）解析式即可求出a．‎ ‎【解答】解：根据条件得：4=﹣a+2；‎ ‎∴a=﹣2．‎ 故答案为：﹣2．‎ ‎【点评】考查函数图象上的点的坐标和函数解析式的关系，考查学生的计算能力，比较基础．‎ ‎　‎ ‎14．（3分）若x，y满足约束条件，则z=2x+y的最大值为　8　．‎ ‎【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定z的最大值．‎ ‎【解答】解：作出不等式组对应的平面区域如图：（阴影部分ABC）．‎ 由z=2x+y得y=﹣2x+z，‎ 平移直线y=﹣2x+z，‎ 由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，‎ 此时z最大．‎ 由，解得，即A（3，2）‎ 将A（3，2）的坐标代入目标函数z=2x+y，‎ 得z=2×3+2=8．即z=2x+y的最大值为8．‎ 故答案为：8．‎ ‎【点评】本题主要考查线性规划的应用，结合目标函数的几何意义，利用数形结合的数学思想是解决此类问题的基本方法．‎ ‎　‎ ‎15．（3分）已知双曲线过点且渐近线方程为y=±x，则该双曲线的标准方程是　x2﹣y2=1　．‎ ‎【分析】设双曲线方程为y2﹣x2=λ，代入点，求出λ，即可求出双曲线的标准方程．‎ ‎【解答】解：设双曲线方程为y2﹣x2=λ，‎ 代入点，可得3﹣=λ，‎ ‎∴λ=﹣1，‎ ‎∴双曲线的标准方程是x2﹣y2=1．‎ 故答案为：x2﹣y2=1．‎ ‎【点评】本题考查双曲线的标准方程，考查学生的计算能力，正确设出双曲线的方程是关键．‎ ‎　‎ ‎16．（3分）已知曲线y=x+lnx在点（1，1）处的切线与曲线y=ax2+（a+2）x+1相切，则a=　8　．‎ ‎【分析】求出y=x+‎ lnx的导数，求得切线的斜率，可得切线方程，再由于切线与曲线y=ax2+（a+2）x+1相切，有且只有一切点，进而可联立切线与曲线方程，根据△=0得到a的值．‎ ‎【解答】解：y=x+lnx的导数为y′=1+，‎ 曲线y=x+lnx在x=1处的切线斜率为k=2，‎ 则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2，即y=2x﹣1．‎ 由于切线与曲线y=ax2+（a+2）x+1相切，‎ 故y=ax2+（a+2）x+1可联立y=2x﹣1，‎ 得ax2+ax+2=0，‎ 又a≠0，两线相切有一切点，‎ 所以有△=a2﹣8a=0，‎ 解得a=8．‎ 故答案为：8．‎ ‎【点评】本题考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处的导数，设出切线方程运用两线相切的性质是解题的关键．‎ ‎　‎ 三．解答题 ‎17．△ABC中，D是BC上的点，AD平分∠BAC，BD=2DC ‎（Ⅰ） 求．‎ ‎（Ⅱ） 若∠BAC=60°，求∠B．‎ ‎【分析】（Ⅰ）由题意画出图形，再由正弦定理结合内角平分线定理得答案；‎ ‎（Ⅱ）由∠C=180°﹣（∠BAC+∠B），两边取正弦后展开两角和的正弦，再结合（Ⅰ）中的结论得答案．‎ ‎【解答】解：（Ⅰ）如图，‎ 由正弦定理得：‎ ‎，‎ ‎∵AD平分∠BAC，BD=2DC，‎ ‎∴；‎ ‎（Ⅱ）∵∠C=180°﹣（∠BAC+∠B），∠BAC=60°，‎ ‎∴，‎ 由（Ⅰ）知2sin∠B=sin∠C，‎ ‎∴tan∠B=，即∠B=30°．‎ ‎【点评】本题考查了内角平分线的性质，考查了正弦定理的应用，是中档题．‎ ‎　‎ ‎18．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表 B地区用户满意度评分的频数分布表 满意度评分分组 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ ‎[90，100）‎ 频数 ‎2‎ ‎8‎ ‎14‎ ‎10‎ ‎6‎ ‎（1）做出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）‎ ‎（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：‎ 满意度评分 低于70分 ‎70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 估计哪个地区用户的满意度等级为不满意的概率大？说明理由．‎ ‎【分析】（I）根据分布表的数据，画出频率直方图，求解即可．‎ ‎（II）计算得出CA表示事件：“A地区用户的满意度等级为不满意”，CB表示事件：“B地区用户的满意度等级为不满意”，‎ P（CA），P（CB），即可判断不满意的情况．‎ ‎【解答】解：（Ⅰ）‎ 通过两个地区用户满意度评分的频率分布直方图可以看出，B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值，‎ B 地区的用户满意度评分的比较集中，而A地区的用户满意度评分的比较分散．‎ ‎（Ⅱ）A地区用户的满意度等级为不满意的概率大．‎ 记CA表示事件：“A地区用户的满意度等级为不满意”，CB表示事件：“B地区用户的满意度等级为不满意”，‎ 由直方图得P（CA）=（0.01+0.02+0.03）×10=0.6‎ 得P（CB）=（0.005+0.02）×10=0.25‎ ‎∴A地区用户的满意度等级为不满意的概率大．‎ ‎【点评】本题考查了频率直方图，频率表达运用，考查了阅读能力，属于中档题．‎ ‎　‎ ‎19．（12分）如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1‎ ‎=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形 ‎（Ⅰ）在图中画出这个正方形（不必说出画法和理由）‎ ‎（Ⅱ）求平面α把该长方体分成的两部分体积的比值．‎ ‎【分析】（Ⅰ）利用平面与平面平行的性质，可在图中画出这个正方形；‎ ‎（Ⅱ）求出MH==6，AH=10，HB=6，即可求平面a把该长方体分成的两部分体积的比值．‎ ‎【解答】解：（Ⅰ）交线围成的正方形EFGH如图所示；‎ ‎（Ⅱ）作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8．‎ 因为EFGH为正方形，所以EH=EF=BC=10，‎ 于是MH==6，AH=10，HB=6．‎ 因为长方体被平面α分成两个高为10的直棱柱，‎ 所以其体积的比值为．‎ ‎【点评】本题考查平面与平面平行的性质，考查学生的计算能力，比较基础．‎ ‎　‎ ‎20．椭圆C：=1，（a＞b＞0）的离心率，点（2，）在C上．‎ ‎（1）求椭圆C的方程；‎ ‎（2）直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值．‎ ‎【分析】（1）利用椭圆的离心率，以及椭圆经过的点，求解椭圆的几何量，然后得到椭圆的方程．‎ ‎（2）设直线l：y=kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），联立直线方程与椭圆方程，通过韦达定理求解KOM，然后推出直线OM的斜率与l的斜率的乘积为定值．‎ ‎【解答】解：（1）椭圆C：=1，（a＞b＞0）的离心率，点（2，）在C上，可得，，解得a2=8，b2=4，所求椭圆C方程为：．‎ ‎（2）设直线l：y=kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），‎ 把直线y=kx+b代入可得（2k2+1）x2+4kbx+2b2﹣8=0，‎ 故xM==，yM=kxM+b=，‎ 于是在OM的斜率为：KOM==，即KOM•k=．‎ ‎∴直线OM的斜率与l的斜率的乘积为定值．‎ ‎【点评】本题考查椭圆方程的综合应用，椭圆的方程的求法，考查分析问题解决问题的能力．‎ ‎　‎ ‎21．设函数f（x）=lnx+a（1﹣x）．‎ ‎（Ⅰ）讨论：f（x）的单调性；‎ ‎（Ⅱ）当f（x）有最大值，且最大值大于2a﹣2时，求a的取值范围．‎ ‎【分析】（Ⅰ）先求导，再分类讨论，根据导数即可判断函数的单调性；‎ ‎（2）先求出函数的最大值，再构造函数（a）=lna+‎ a﹣1，根据函数的单调性即可求出a的范围．‎ ‎【解答】解：（Ⅰ）f（x）=lnx+a（1﹣x）的定义域为（0，+∞），‎ ‎∴f′（x）=﹣a=，‎ 若a≤0，则f′（x）＞0，∴函数f（x）在（0，+∞）上单调递增，‎ 若a＞0，则当x∈（0，）时，f′（x）＞0，当x∈（，+∞）时，f′（x）＜0，所以f（x）在（0，）上单调递增，在（，+∞）上单调递减，‎ ‎（Ⅱ），由（Ⅰ）知，当a≤0时，f（x）在（0，+∞）上无最大值；当a＞0时，f（x）在x=取得最大值，最大值为f（）=﹣lna+a﹣1，‎ ‎∵f（）＞2a﹣2，‎ ‎∴lna+a﹣1＜0，‎ 令g（a）=lna+a﹣1，‎ ‎∵g（a）在（0，+∞）单调递增，g（1）=0，‎ ‎∴当0＜a＜1时，g（a）＜0，‎ 当a＞1时，g（a）＞0，‎ ‎∴a的取值范围为（0，1）．‎ ‎【点评】本题考查了导数与函数的单调性最值的关系，以及参数的取值范围，属于中档题．‎ ‎　‎ 四、选修4-1：几何证明选讲 ‎22．（10分）如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．‎ ‎（1）证明：EF∥BC；‎ ‎（2）若AG等于⊙O的半径，且AE=MN=2，求四边形EBCF的面积．‎ ‎【分析】（1）通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F，利用相似的性质即得结论；‎ ‎（2）通过（1）知AD是EF的垂直平分线，连结OE、OM，则OE⊥AE，利用S△ABC﹣S△AEF计算即可．‎ ‎【解答】（1）证明：∵△ABC为等腰三角形，AD⊥BC，‎ ‎∴AD是∠CAB的角平分线，‎ 又∵圆O分别与AB、AC相切于点E、F，‎ ‎∴AE=AF，∴AD⊥EF，‎ ‎∴EF∥BC；‎ ‎（2）解：由（1）知AE=AF，AD⊥EF，∴AD是EF的垂直平分线，‎ 又∵EF为圆O的弦，∴O在AD上，‎ 连结OE、OM，则OE⊥AE，‎ 由AG等于圆O的半径可得AO=2OE，‎ ‎∴∠OAE=30°，∴△ABC与△AEF都是等边三角形，‎ ‎∵AE=2，∴AO=4，OE=2，‎ ‎∵OM=OE=2，DM=MN=，∴OD=1，‎ ‎∴AD=5，AB=，‎ ‎∴四边形EBCF的面积为×﹣××=．‎ ‎【点评】本题考查空间中线与线之间的位置关系，考查四边形面积的计算，注意解题方法的积累，属于中档题．‎ ‎　‎ 五、选修4-4：坐标系与参数方程 ‎23．（10分）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2cosθ．‎ ‎（1）求C2与C3交点的直角坐标；‎ ‎（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．‎ ‎【分析】（I）由曲线C2：ρ=2sinθ，化为ρ2=2ρsinθ，把代入可得直角坐标方程．同理由C3：ρ=2cosθ．可得直角坐标方程，联立解出可得C2与C3交点的直角坐标．‎ ‎（2）由曲线C1的参数方程，消去参数t，化为普通方程：y=xtanα，其中0≤α≤π，α≠；α=时，为x=0（y≠0）．其极坐标方程为：θ=α（ρ∈R，ρ≠0），利用|AB|=即可得出．‎ ‎【解答】解：（I）由曲线C2：ρ=2sinθ，化为ρ2=2ρsinθ，‎ ‎∴x2+y2=2y．‎ 同理由C3：ρ=2cosθ．可得直角坐标方程：，‎ 联立，‎ 解得，，‎ ‎∴C2与C3交点的直角坐标为（0，0），．‎ ‎（2）曲线C1：（t为参数，t≠0），化为普通方程：y=xtanα，其中0≤α≤π，α≠；α=时，为x=0（y≠0）．其极坐标方程为：θ=α（ρ∈R，ρ≠0），‎ ‎∵A，B都在C1上，‎ ‎∴A（2sinα，α），B．‎ ‎∴|AB|==4，‎ 当时，|AB|取得最大值4．‎ ‎【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ 六、选修4-5不等式选讲 ‎24．（10分）设a，b，c，d均为正数，且a+b=c+d，证明：‎ ‎（1）若ab＞cd，则+＞+；‎ ‎（2）+＞+是|a﹣b|＜|c﹣d|的充要条件．‎ ‎【分析】（1）运用不等式的性质，结合条件a，b，c，d均为正数，且a+b=c+d，ab＞cd，即可得证；‎ ‎（2）从两方面证，①若+＞+，证得|a﹣b|＜|c﹣d|，②若|a﹣b|＜|c﹣d|，证得+＞+，注意运用不等式的性质，即可得证．‎ ‎【解答】证明：（1）由于（+）2=a+b+2，‎ ‎（+）2=c+d+2，‎ 由a，b，c，d均为正数，且a+b=c+d，ab＞cd，‎ 则＞，‎ 即有（+）2＞（+）2，‎ 则+＞+；‎ ‎（2）①若+＞+，则（+）2＞（+）2，‎ 即为a+b+2＞c+d+2，‎ 由a+b=c+d，则ab＞cd，‎ 于是（a﹣b）2=（a+b）2﹣4ab，‎ ‎（c﹣d）2=（c+d）2﹣4cd，‎ 即有（a﹣b）2＜（c﹣d）2，即为|a﹣b|＜|c﹣d|；‎ ‎②若|a﹣b|＜|c﹣d|，则（a﹣b）2＜（c﹣d）2，‎ 即有（a+b）2﹣4ab＜（c+d）2﹣4cd，‎ 由a+b=c+d，则ab＞cd，‎ 则有（+）2＞（+）2．‎ 综上可得，+＞+是|a﹣b|＜|c﹣d|的充要条件．‎ ‎【点评】本题考查不等式的证明，主要考查不等式的性质的运用，同时考查充要条件的判断，属于基础题．‎ ‎　‎