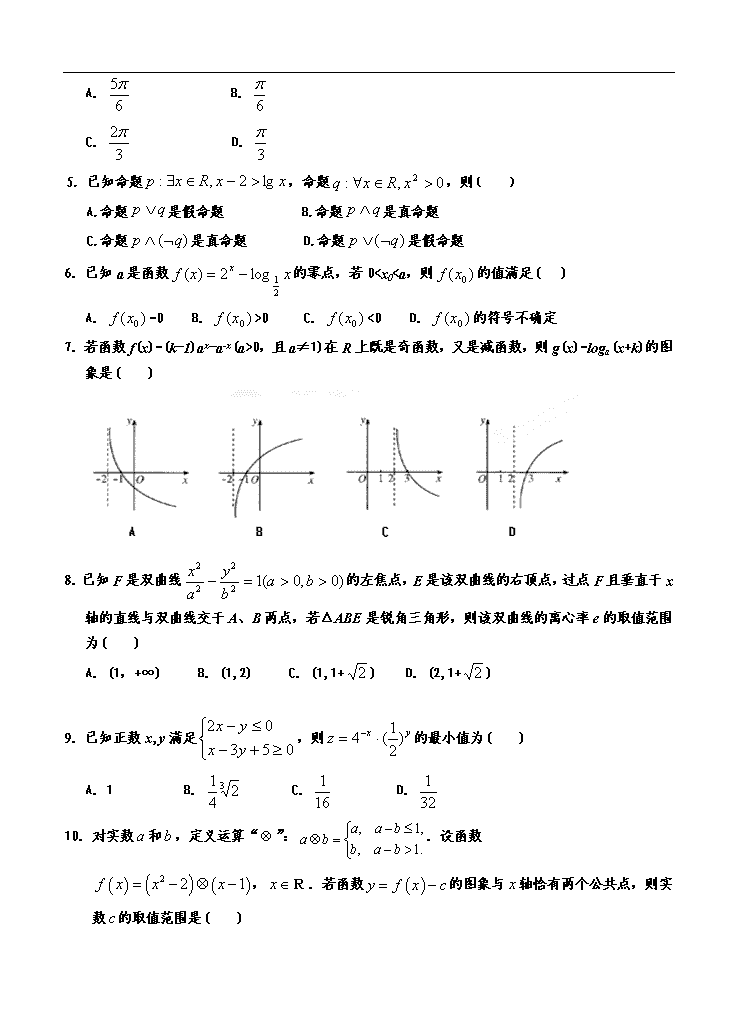宁夏银川一中2013届高三第二次模拟数学(文)试题
第I卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合A={x|x2+3x+2≤0},B={y|y=2x-1,x∈R},则A∩CRB=( )
A. B.{-1} C.[-2,-1] D.[-2,-1)
2.若复数的实部与虚部相等,则实数b等于( )
A.3 B. 1 C. D.
3.一个几何体的三视图及其尺寸(单位:cm)
如图所示,则该几何体的侧面积为( )cm2。
A.48 B.12 C.80 D.20
4.若将函数的图象
向右平移m(0
0 C.<0 D.的符号不确定
7.若函数f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的图象是( )
8.已知F是双曲线的左焦点,E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,若ΔABE是锐角三角形,则该双曲线的离心率e的取值范围为( )
A.(1,+∞) B.(1,2) C.(1,1+) D.(2,1+)
9.已知正数x,y满足,则的最小值为( )
A.1 B. C. D.
10.对实数和,定义运算“”:.设函数
,.若函数的图象与轴恰有两个公共点,则实数的取值范围是( )
A. B. C. D.
11.定义在R上的函数f(x)满足f(x)=f(x+2),且当x∈[3,5]时,f(x)=2-|x-4|,则( )
A. B.
C. D.
12.已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称,若任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
A.(3,7) B. (9,25) C. (13,49) D. (9, 49)
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第
21题为必考题,每个试题考生都必须做答.第22题
~第24题为选考题,考生根据要求做答.
二、填空题:本大题共4小题,每小题5分.
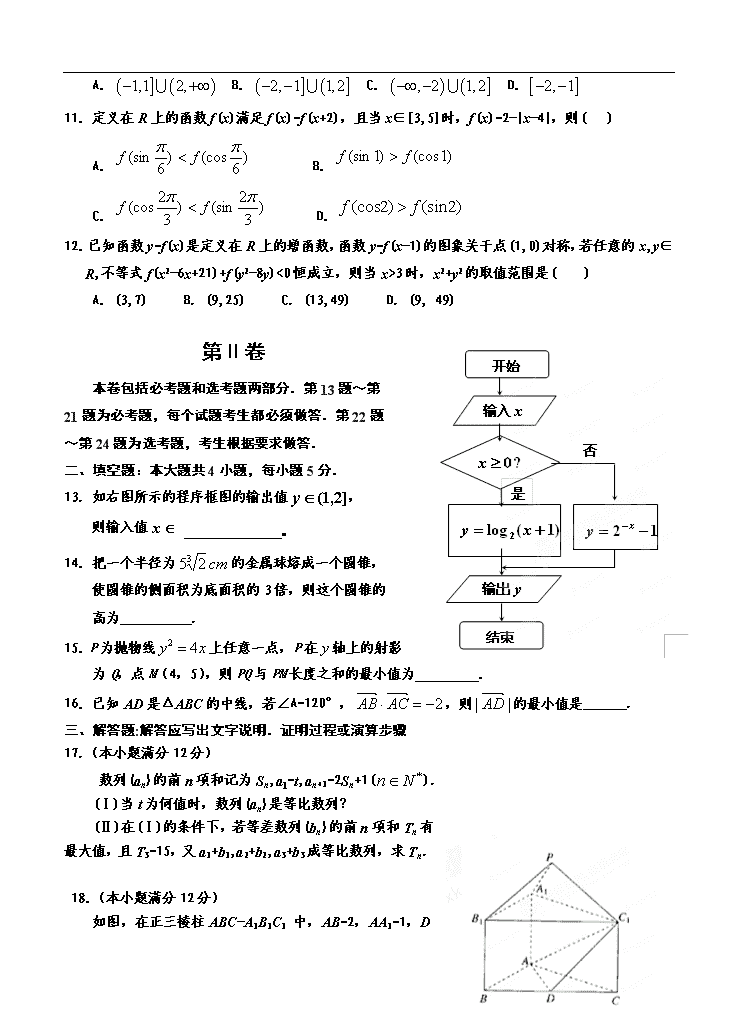
13. 如右图所示的程序框图的输出值,
则输入值 。
14.把一个半径为的金属球熔成一个圆锥,
使圆锥的侧面积为底面积的3倍,则这个圆锥的
高为__________.
15.P为抛物线上任意一点,P在轴上的射影为Q,点M(4,5),则PQ与PM长度之和的最小值为 .
16.已知AD是ΔABC的中线,若∠A=120°,,则的最小值是______.
三、解答题:解答应写出文字说明.证明过程或演算步骤
17.(本小题满分12分)
数列{an}的前n项和记为Sn,a1=t,an+1=2Sn+1().
(Ⅰ)当t为何值时,数列{an}是等比数列?
(Ⅱ)在(Ⅰ)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1,a2+b2,a3+b3成等比数列,求Tn.
18.(本小题满分12分)
如图,在正三棱柱ABC-A1B1C1 中,AB=2,AA1=1,D
是
BC的中点,点P在平面BCC1B1内,PB1=PC1=.
(Ⅰ)求证:PA1⊥BC;
(Ⅱ)求证:PB1∥平面AC1D;
(Ⅲ)求.
19.(本小题满分12分)
从某学校的名男生中随机抽
取名测量身高,被测学生身高全部
介于cm和cm之间,将测量结
果按如下方式分成八组:第一组
[,),第二组[,),
…,第八组[,],右图是按上
述分组方法得到的频率分布直方图的
一部分,已知第一组与第八组人数相同,
第六组的人数为人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的名男生的身高的中位数以及身高在cm以上(含cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,事件{},事件{},求.
20. (本小题满分12分)
如图,在直角坐标系xOy中,点P到抛物线C:y2=2px(p>0)的准线的距离为.点M(t,1)是C上的定点,A,B是C上的两动点,
且线段AB被直线OM平分.
(1)求p,t的值;
(2)求△ABP面积的最大值.
21.(本小题满分12分)
设.
(I)若a>0,讨论的单调性;
(Ⅱ)x =1时,有极值,证明:当∈[0,]时,
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
22.(本小题满分10分) 选修4—1:几何证明选讲.
如图,在RtΔABC中,∠C=90°,BE平分∠ABC,交AC于点E,
点D在AB上,DE⊥EB.
(Ⅰ)求证:AC是ΔBDE的外接圆的切线;
(Ⅱ)若AD=,AE=6,求EC的长.
23.(本小题满分10分)选修4—4:坐标系与参数方程.
已知曲线C的极坐标方程为,直线的参数方程为( t为参数,0≤<).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线经过点(1,0),求直线被曲线C截得的线段AB的长.
24.(本小题满分10分)选修4—5:不等式选讲.
设函数f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若的定义域为R,求实数m的取值范围.
三、解答题: