2018-2019学年内蒙古巴彦淖尔市临河三中高二下学期期中考试数学（理）试题 word版

2018-2019学年内蒙古巴彦淖尔市临河三中高二下学期期中考试数学（理）试题 word版

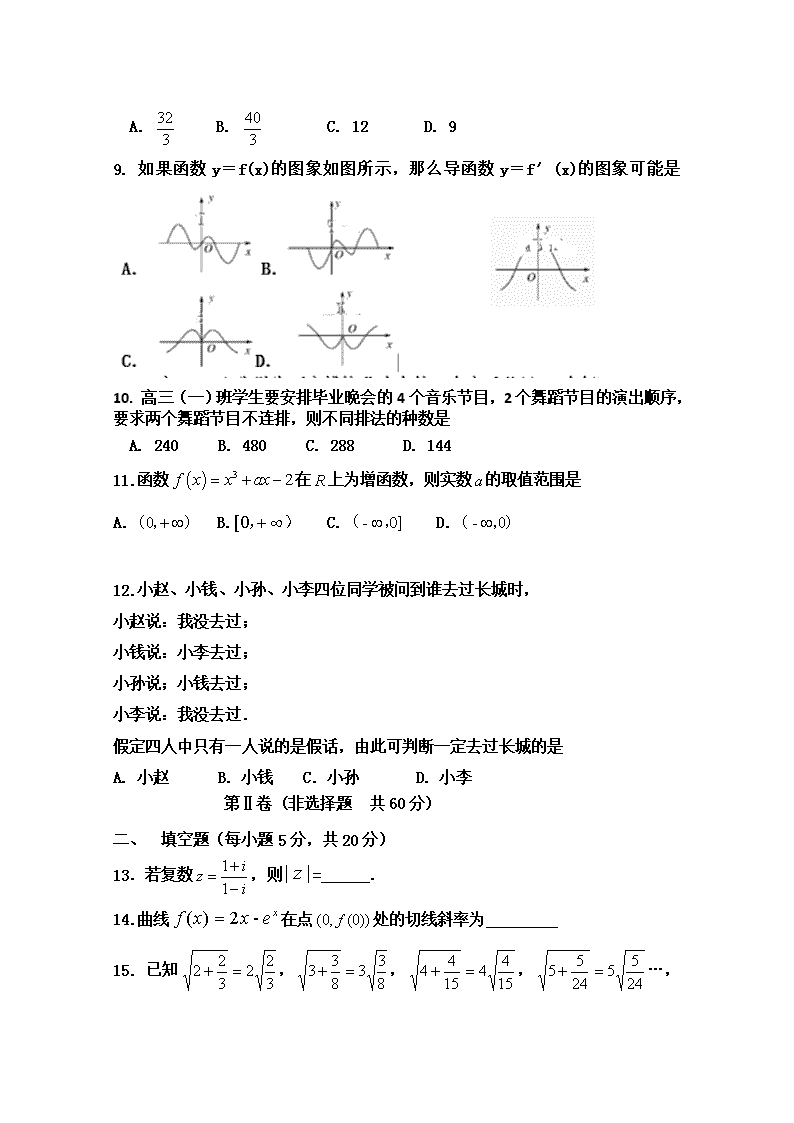
临河三中2018-2019学年第二学期期中 高二数学（理科普通）试题 ‎ ‎ ‎ 第Ⅰ卷（选择题 共60分）‎ 一、 选择题（每小题5分，共60分）‎ ‎1．若复数满足，则的共轭复数为 ‎ A． B． C． D．‎ ‎2. 已知向量＝（1，﹣1，3）与＝（-2，λ，-6）平行，则实数λ的值为 ‎ ‎ A．2 B．-2 C． 20 D．-20‎ ‎3．下面三段话可组成“三段论”，则“小前提”是 ①因为指数函数是增函数； ②所以是增函数；③而是指数函数．‎ ‎ A. ① B.② C.③ D.①② ‎ ‎4．定积分 = ‎ ‎ A． B. C． D．‎ ‎5.若，则的递增区间是 ‎ ‎ A. B. C. D.‎ ‎6.用数字1，2，3，4，5可以组成没有重复数字的五位偶数共有 ‎ ‎ A．36个 B.18个 C. 24个 D．48个 ‎7.长方体中,,,为的中点，则异面直线与所成角的余弦值为 ‎ ‎ A． B． C． D．‎ ‎8．由函数的图像、轴以及直线、所围成的封闭图形的面积是 ‎ A. B. C. 12 D. 9‎ ‎9. 如果函数y＝f(x)的图象如图所示，那么导函数y＝f′(x)的图象可能是 ‎ ‎10. 高三（一）班学生要安排毕业晚会的4个音乐节目，2个舞蹈节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是 ‎ ‎ A. 240 B. 480 C. 288 D. 144‎ ‎11.函数在上为增函数，则实数的取值范围是 ‎ A． B. C． D．‎ ‎12.小赵、小钱、小孙、小李四位同学被问到谁去过长城时，‎ 小赵说：我没去过； ‎ 小钱说：小李去过；‎ 小孙说；小钱去过； ‎ 小李说：我没去过． 假定四人中只有一人说的是假话，由此可判断一定去过长城的是 ‎ A. 小赵 B. 小钱 C. 小孙 D. 小李 第Ⅱ卷 (非选择题　共60分)‎ 一、 填空题（每小题5分，共20分）‎ ‎13．若复数，则=______． ‎ ‎14.曲线在点处的切线斜率为 ‎ ‎15. 已知，，，…‎ ‎，类比这些等式，若，则_____ ‎ ‎16.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排, 2位老人相邻但不排在两端,不同的排法共有_____ 种（用数字作答）‎ 三、解答题 (解答应写出文字说明，证明过程或演算步骤。 )‎ ‎17．（本题10分）已知复数.‎ ‎（1）若为纯虚数，求实数的值； （2）若在复平面上对应的点在直线上，求实数的值 18. （本题10分）已知函数，曲线在点处的切线方程为.‎ ‎(1)求,的值；‎ ‎(2)求函数在上的最大值.‎ ‎19．（本题10分）‎ 如图，四棱锥P—ABCD中，底面ABCD为矩形，‎ 且PA=AD=4,AB=2,PA⊥平面ABCD，E是PD的中点．‎ ‎（1）证明：CD⊥PD ‎（2）求二面角E—AC—D的余弦值．‎ ‎20.（本题10分）已知，函数，，且是函数的极大值点． （1）求的值， （2）如果函数和函数在区间上均为增函数，求实数的取值范围．‎ 临河三中2018-2019学年第二学期期中 ‎ 高二数学（理科普通）试题答案 一、 选择题（每题5分）：‎ ‎1--5 D A C A C 6--10 D C A A B 11--12 B B 二、填空题（每题5分）：‎ ‎13) 1 14) 1 15) 48 16) 960‎ 三、解答题(每题10分)‎ ‎17.解：（1）若z为纯虚数，则，且，解得:； （2）z在复平面上对应的点（，）， 在直线上，则,‎ 即,解得 ‎18. 解：(1)因为切点为，所以 即，，‎ 又， ‎ 而由切线方程的斜率可知，‎ ‎，即 由解得.‎ ‎(2)由（1）知，‎ 令得或.‎ 当时，得或，‎ ‎ 即在，上单调递增；‎ 当时，得，‎ 即在上单调递减.‎ 因此的极大值为，极小值为.‎ 又，，‎ 故函数在上的最大值为13.‎ ‎19. 解：（1）因为PA⊥平面ABCD，底面ABCD为矩形，‎ 所以AB、AD、AP两两垂直，以A为坐标原点，‎ 建立如图所示的空间直角坐标系A－xyz，‎ 则A（0，0，0），C（2，4，0），D（0，4，0），‎ ‎ P（0，0，4），E（0,2,2）‎ 所以=（-2,0,0），＝（0,4,-4）‎ ‎,即 ‎（2）由（1）得：，‎ 设平面AEC的一个法向量为，‎ 则，因此 取，解得则 因为PA⊥平面ABCD，所以为平面ACD的一个法向量．‎ 又，所以．‎ 因为二面角E—AC—D为锐角，所以所求二面角的余弦值为．‎ ‎20.解：（1）因为函数，‎ 所以， 又因为是函数的极大值点． 所以，解得 检验：当时，， 当时，，当时，， 所以是函数的极大值点，符合题意．‎ 所以 ‎. （2），‎ 所以函数的单调递增区间是. 又由（1）可知函数的单调递增区间是， 所以依题意得或 解得或.‎ 所以实数的取值范围是{0}∪[2，3] ‎