河南省开封市五县联考2019-2020学年高一下学期期末考试数学试题 Word版含答案

河南省开封市五县联考2019-2020学年高一下学期期末考试数学试题 Word版含答案

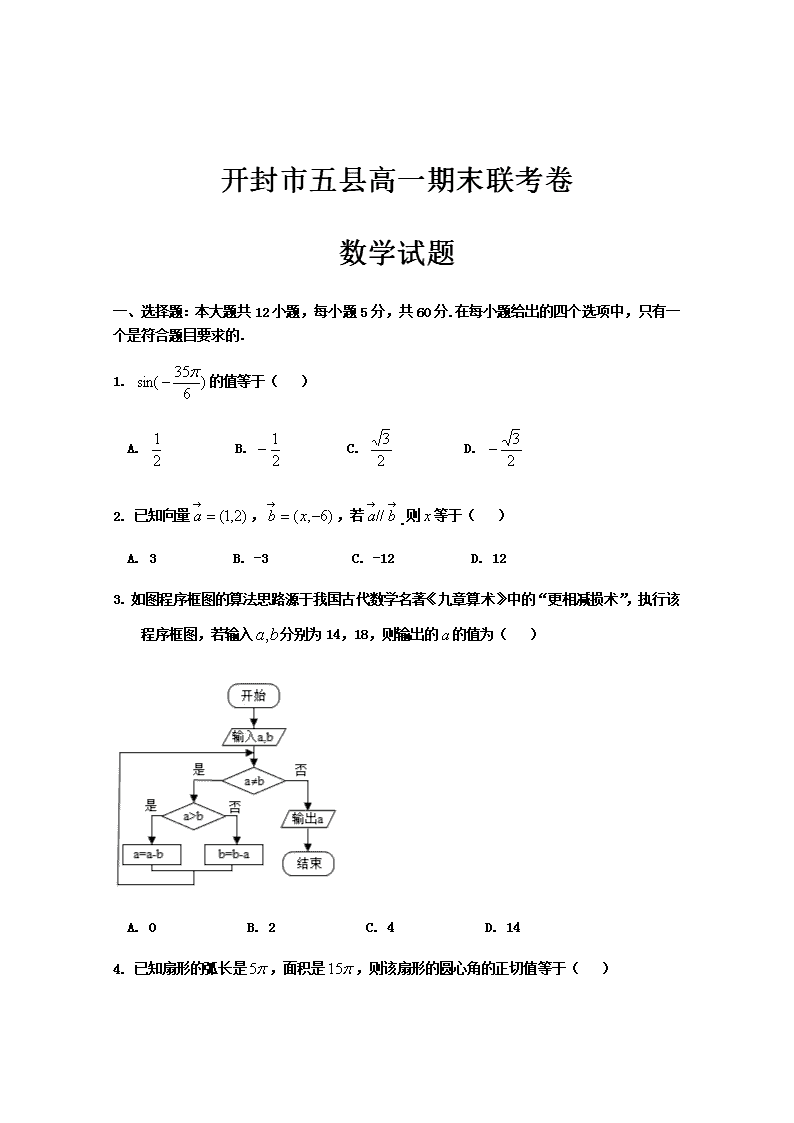
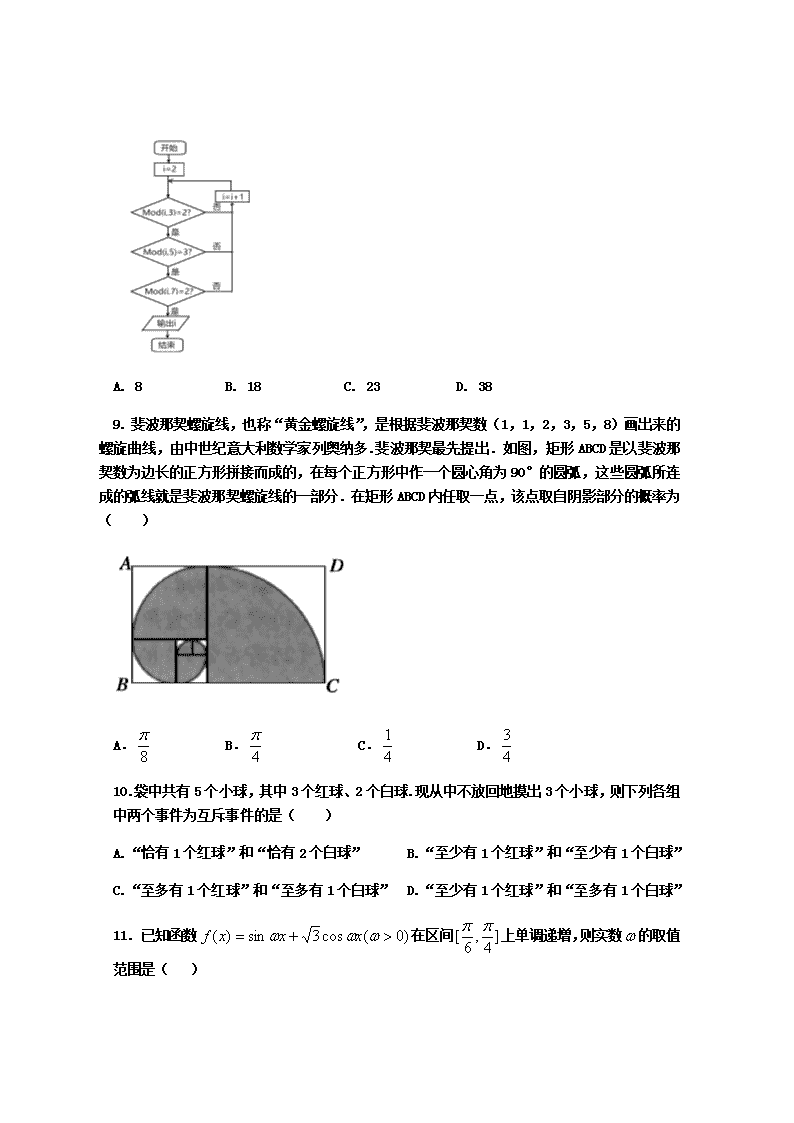
开封市五县高一期末联考卷 数学试题 一、 选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个是符合题目要求的.‎ 1. 的值等于（ ）‎ A. ‎ B. C. D. ‎ 2. 已知向量，，若.则等于（ ）‎ A. ‎3 B. -3 C. -12 D. 12‎ 3. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入分别为14，18，则输出的的值为（ ）‎ A. ‎0 B. 2 C. 4 D. 14 ‎ 4. 已知扇形的弧长是，面积是，则该扇形的圆心角的正切值等于（ ）‎ A. B. C. D. ‎ 3. 为了解高一学生对《中华人民共和国民法典》的学习情况，现从某校高一1205名学生中抽取50名学生参加测试，则首先用简单随机抽样剔除5名学生，然后剩余的1200名学生再用系统抽样的方法抽取，则每人入选的概率（ ）‎ A. 不全相等 B. 均不相等 C. 都相等，为 D. 都相等，为 ‎6. 设函数在的图象大致如图所示，则的最小正周期为（ ）‎ A． B． C． D．‎ ‎7. 已知变量与正相关，且由观测数据求得。由观测数据得出的线性回归方程可能是（ ） ‎ A. ‎ B. C. D. ‎ 8. ‎ 若正整数N除以正整数m后的余数为r，则记为，例如 .如图所示的程序框图的算法源于我国古代数学名著《孙子算经》中的“中国剩余定理”，则执行该程序框图输出的的值为（ ）‎ A. 8 B. 18 C. 23 D. 38‎ ‎9. 斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数（1，1，2，3，5，8）画出来的螺旋曲线，由中世纪意大利数学家列奥纳多.斐波那契最先提出．如图，矩形ABCD是以斐波那契数为边长的正方形拼接而成的，在每个正方形中作一个圆心角为90°的圆弧，这些圆弧所连成的弧线就是斐波那契螺旋线的一部分．在矩形ABCD内任取一点，该点取自阴影部分的概率为（　　）‎ A． ‎ B． C． D．‎ ‎10.袋中共有5个小球，其中3个红球、2个白球.现从中不放回地摸出3个小球，则下列各组中两个事件为互斥事件的是（ ）‎ A.“恰有1个红球”和“恰有2个白球” B.“至少有1个红球”和“至少有1个白球”‎ C.“至多有1个红球”和“至多有1个白球” D.“至少有1个红球”和“至多有1个白球”‎ ‎11. 已知函数在区间上单调递增，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎12.已知 是平面上一定点，是平面上不共线的三个点，动点满足，则点的轨迹一定通过的（ ）‎ A. 外心 B.内心 C.重心 D. 垂心 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎13. 雷神山医院从开始设计到建成完工，历时仅十天。完工后，新华社记者要对部分参与人员采访。决定从300名机械车操控人员，160名管理人员和240名工人中按照分层抽样的方法抽取35人，则从工人中抽取的人数为 ；‎ ‎14. 已知向量满足，则向量在方向上的投影为 ；‎ ‎15. 新冠肺炎疫情爆发后，某市指定医院组织市民进行核糖核酸检测。某个检测点派出了两名医生，四名护士。把这六名医护人员分为两组，每组一名医生，两名护士，则医生甲与护士乙分在一组的概率为 ；‎ ‎16. 已知函数，给出下列四个结论：‎ ‎①函数是最小正周期为的奇函数；‎ ‎②直线是函数的一条对称轴；‎ ‎③点是函数的一个对称中心；‎ ‎④函数的单调递减区间为 其中正确的结论是 （填序号）.‎ 三、解答题：本大题共6小题，共70分。解答题写出文字说明、证明过程或演算步骤。‎ ‎17.（本小题10分）已知角.求下列各式的值.‎ ‎(1) 求的值；‎ ‎(2) 先化简，再求值．‎ ‎18.（本小题12分）如图，已知在中，是的中点，是线段的靠近点的三等分点，和交于点，设.‎ （1） ‎ 用和表示向量.‎ （2） ‎ 若，求实数的值.‎ ‎19.（本小题12分）为庆祝国庆节，某中学团委组织了“歌颂祖国，爱我中华”知识竞赛，从参加考试的学生中抽出60名，将其成绩(成绩均为整数)分成[40，50)，[50，60)，…，[90，100]六组，并画出如图所示的部分频率分布直方图，观察图形，回答下列问题：‎ （1） 求第四组的频率，并补全这个频率分布直方图；‎ （2） 请根据频率分布直方图，估计样本的中位数和方差．（每组数据以区间的中点值为代表）. ‎ ‎20.（本小题12分）已知函数，其图象与轴相邻两个交点的距离为.‎ ‎（1）求函数的解析式；‎ ‎（2）若将的图象向左平移个单位长度得到函数的图象恰好经过点 ‎，求当取得最小值时，在上的单调递增区间.‎ ‎ 21.（本小题12分） 是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物），为了探究车流量与的浓度是否相关，现采集到某城市周一至周五某时间段车流量与的浓度数据如下表：‎ 时间 周一 周二 周三 周四 周五 车流量（万辆）‎ ‎50‎ ‎51‎ ‎54‎ ‎57‎ ‎58‎ 的浓度（微克/立方米）‎ ‎39‎ ‎40‎ ‎42‎ ‎44‎ ‎45‎ ‎（1）根据上表数据，求出这五组数据组成的散点图的样本中心坐标；‎ ‎（2）用最小二乘法求出关于的线性回归方程；‎ ‎（3）若周六同一时间段车流量是100万辆，试根据（2）求出的线性回归方程预测，此时的浓度是多少？‎ ‎（参考公式：，）‎ ‎22.（本小题12分）在如图所示的平面直角坐标系中，已知点A(1,0)和点B(－1，0)，||＝1，且，其中O为坐标原点．‎ (1) 若，设点D为线段OA上的动点，求|＋|的最小值；‎ (2) 若，向量＝，，求的最小值及对应的x值．‎ 开封市五县高一期末联考卷参考答案 一．选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B B D C C D C B C B D 二． 填空题 13. ‎ 12 ； 14. -1 ； 15. ； 16. ② .‎ 三． 解答题 17. 解：（1）‎ ‎(2)‎ 由（1）知 ‎ 17. ‎（1）‎ ‎,‎ (2) 设 ‎ ‎ 又，且不共线.‎ 所以由平面向量基本定理知：‎ 19. 解:(1)因为各组的频率和等于1，所以第四组的频率为 .‎ 补全的频率分布直方图如图所示．‎ ‎（2）前三组的频率之和为：‎ ‎ 前四组的频率之和为：‎ 设中位数为,则应有 又， 即样本的中位数为 抽取学生的平均数约为所以，样本的方差为：‎ 19. 解：（1）‎ ‎ ‎ ‎ ‎ 因为函数的图象与轴相邻的两个交点之间的距离为 即 从而函数的解析式为：‎ （2） 的图象是由的图象向左平移个单位长度得到，所以有： ‎ ‎，即 此时，‎ 令得 所以在上的单调增区间为：‎ 21. 解：（1）‎ ‎ ‎ 所以样本中心坐标为.‎ ‎(2) 因为 ‎，‎ 所以， ‎ 线性回归方程为.‎ ‎（3）（微克/立方米）‎ 此时的浓度是75.12微克/立方米.‎ ‎22.解：(1)设D(t,0)(0≤t≤1)，又可求得C，‎ 所以＋＝，‎ 所以|＋|2＝－t＋t2＋＝t2－t＋1＝＋(0≤t≤1)，‎ 所以当t＝时，|＋|取得最小值，最小值为. ‎ ‎(2)由题意得C(cos x，sin x)，＝＝(cos x＋1，sin x)，‎ 因为x∈，所以≤2x＋≤，‎ 所以当2x＋＝，即x＝时，sin取得最大值1，‎ 取得最小值1－.‎ 所以的最小值为1－，此时. ‎