- 2021-06-22 发布 |
- 37.5 KB |
- 7页


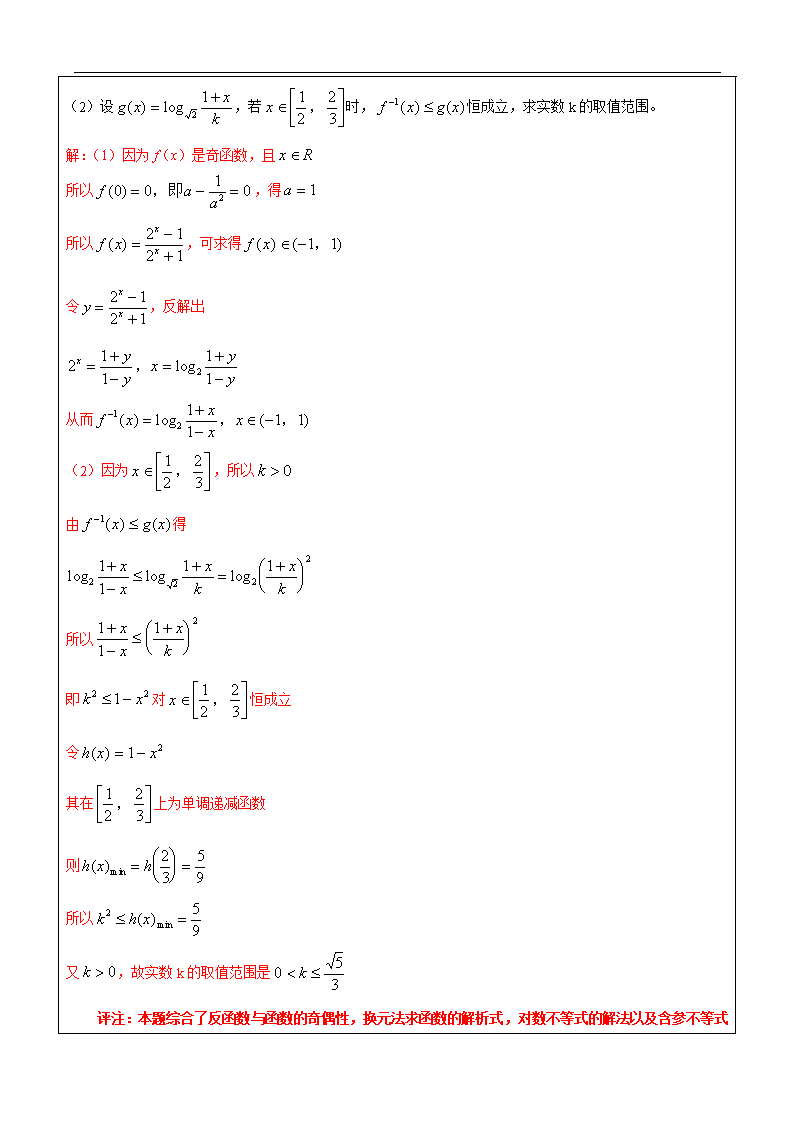
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一数学教案:第2讲 对数函数综合
辅导教案 学员姓名: 学科教师: 年 级: 辅导科目: 授课日期 ××年××月××日 时 间 A / B / C / D / E / F段 主 题 对数函数综合 教学内容 1. 熟练掌握对数函数的性质; 2. 会应用对数函数的图像与性质解决综合问题。 (以提问的形式回顾) 1. 解决与对数函数有关的问题,有哪些需要注意的地方? 解决与对数函数有关的问题,要特别重视定义域,同时注意底数与1的大小关系 2. 底数互为倒数的两个对数函数的图像有什么特点? 底数互为倒数的两个对数函数的图像关于轴对称 3. 已知在上是的减函数,则的取值范围是什么? 由于 在上时 有意义,又是减函数,∴时,取最小值是,∴综上可知所求的取值范围是。 此部分让学生回答,如出现学生不会的问题,可相互讨论,结合教师引导,5到10分钟完成。 (采用教师引导,学生轮流回答的形式) 例1.在函数中,若函数在内为增函数,则实数的取值范围是 . 答案:. 注意隐含条件函数在内都都大于0. 试一试:若函数在区间上是增函数,则的取值范围是 。 答案: 例2. 若函数的定义域为,则的取值范围是 . 解:当时,满足题意;当时,有,解得, 所以的取值范围是. 试一试:若函数的值域为,则的取值范围是 . 由 得,所以的取值范围是 例3. 设不等式时,求的最大值和最小值. 解: 即 ∴即 又 ∵∴ ∴当即时;当,即时,。 【利用换元的整体思想,将视为一个整体。】 例4. 设,f(x)是奇函数,且。 (1)试求f(x)的反函数f-1(x)的解析式及f-1(x)的定义域; (2)设,若时,恒成立,求实数k的取值范围。 解:(1)因为f(x)是奇函数,且 所以,得 所以,可求得 令,反解出 从而 (2)因为,所以 由得 所以 即对恒成立 令 其在上为单调递减函数 则 所以 又,故实数k的取值范围是 评注:本题综合了反函数与函数的奇偶性,换元法求函数的解析式,对数不等式的解法以及含参不等式在定区间上恒成立等知识,是一道综合性较强的好题。 (学生统一完成,互相批改,教师针对重难点详细讲解) 1. 已知是上的增函数,那么的取值范围是( ) D (A) ; (B) ; (C) ; (D) . 2. 已知函数,若,且,则的取值范围是________. 3. 已知 (1) 求函数的定义域和值域; (2) 判断函数在定义域上的单调性. 分析:解指数不等式可得定义域,再求值域;先利用特值判断单调性再利用定义证明即可. 解:(1)由且,解得,故的定义域为; 又,,即, 的值域为. (2)在上是单调减函数,证明如下:设,则: , ,则,即,, 故函数在上是减函数. 利用定义来证明函数的单调性,注意步骤要完整;解不等式时要注意原函数的定义域的限制. 4. 已知函数. (1)当m=7时,求函数f(x)的定义域; (2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围. 解:(1)由题设知:当m=5时:|x+1|+|x﹣2|>7, 不等式的解集是以下三个不等式组解集的并集: , 或, 或, 解得函数f(x)的定义域为(﹣∞,﹣3)∪(4,+∞); (2)不等式f(x)≥2即|x+1|+|x﹣2|≥m+4, ∵x∈R时,恒有|x+1|+|x﹣2|≥|(x+1)﹣(x﹣2)|=3, ∴不等式|x+1|+|x﹣2|≥m+4解集是R,等价于m+4≤3, ∴m的取值范围是(﹣∞,﹣1]. 本节课主要知识:复合函数单调区间的确定与应用,应用换元发求解函数的最大值,最小值 【巩固练习】 1. 已知函数当时,函数的零点 . 2. 已知函数的定义域为R,值域为[0,2],求m,n的值 由,得,即. ∵,即。由0,得 ,由根与系数的关系得,解得m=n=5。 3. 设 (1)当m=1时,求函数f(x)的定义域; (2)若当恒成立,求实数m的取值范围. 解:(1)由题设知:, ∴ ①,或 ②,或 ③. 解①可得 ,解②可得,解③可得 x<0. 不等式的解集是以下三个不等式组解集的并集,求得函数的定义域为 (﹣∞,0)∪(5,+∞). (2)不等式 即,即. ∵,∴,即 . 由于函数 在[1,]上是增函数,故当x=1时,y 取得最小值为4; 当时,y 取得最大值为13, 由题意可得,m大于或等于y的最大值13,故m的取值范围是[13,+∞). 【预习思考】 类型 指数方程的解法 对数方程的解法 最简型 关于x 的方程的解为 . 关于x 的方程的解为 . 同底型 与 方程是同解方程 与 方程是同解方程 换元型 关于x 的方程,设 ,解方程 =0,再解方程 关于x 的方程,设 ,解方程 =0,再解方程查看更多