2017-2018学年广东省惠阳高级中学高二上学期期中考试 数学（理）

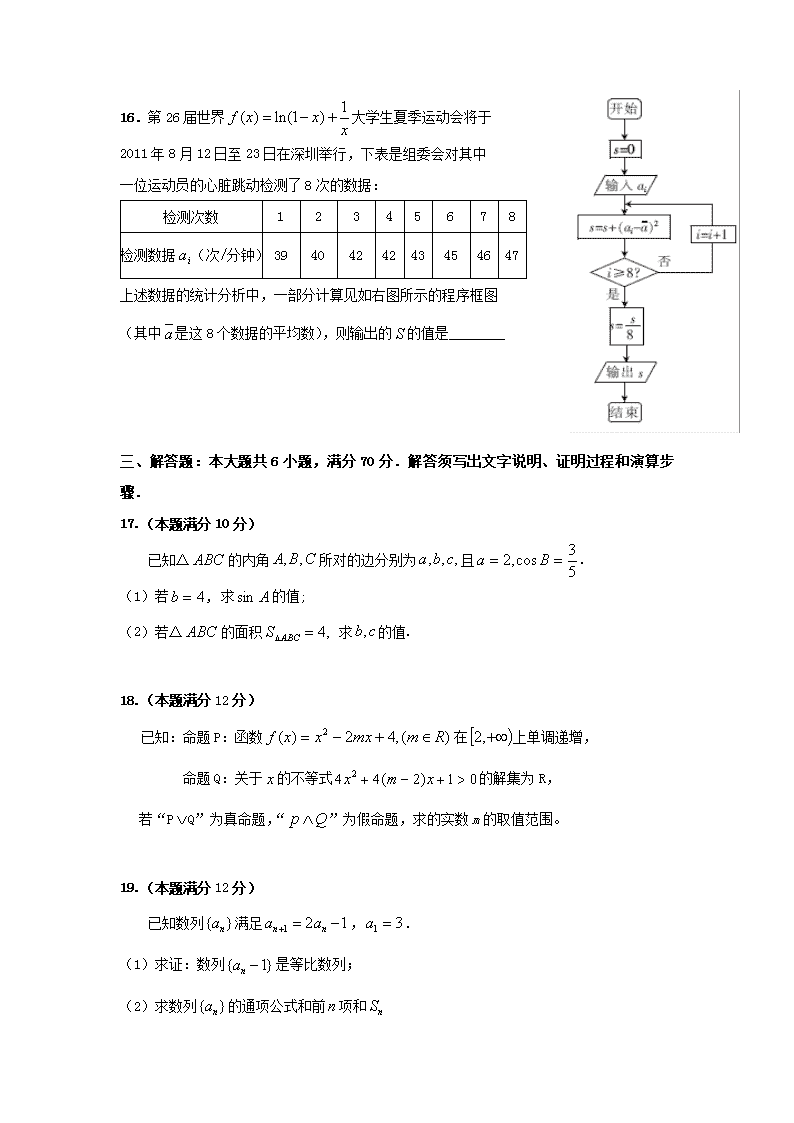
2017-2018学年广东省惠阳高级中学高二上学期期中考试 数学（理）

‎2017-2018学年广东省惠阳高级中学高二上学期期中考试 数学（理）‎ 说明：‎ ‎1.全卷满分150分，时间120 分钟；‎ ‎2.答卷前，考生务必将自己的姓名、原班级、试室、座位号，填写在答题卷上；‎ 参考公式：锥体的体积公式： （是锥体的底面积，是锥体的高） ‎ 一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.‎ ‎1．设集合，若集合 ，则集合的个数为（ ）‎ A． B． C． D．‎ ‎2．已知向量，若∥，则=（ ）‎ A． B. C． D．‎ ‎3．设是公差为正数的等差数列，若，且，则（ ）‎ A． B． C． D．‎ ‎4．下列说法中，正确的是( )．‎ A．数据5，4，4，3，5，2的众数是4‎ B．一组数据的标准差是这组数据的方差的平方 C．数据2，3，4，5的标准差是数据4，6，8，10的标准差的一半 D．频率分布直方图中各小长方形的面积等于相应各组的频数 ‎5．设是椭圆上的点．若是椭圆的两个焦点，则等于( )‎ A.4 B‎.5 ‎ C.8 D.10‎ ‎6．下列说法中,不正确的是（ ）‎ A．“若，则”的逆命题为真命题 B．“”是“”的充分不必要条件 C．命题，，则，‎ D．命题所有有理数都是实数，正数的对数都是负数，则为真命题.‎ ‎7．已知幂函数的图象过点，则的值为（ ）‎ A． B. C． D．‎ ‎8．函数是( )‎ A．最小正周期为的奇函数 B．最小正周期为的欧函数 C．最小正周期为的奇函数 D．最小正周期为的偶函数 ‎ ‎9. 方程有实根的概率为（ ）．‎ A. B. C. D.‎ 正(主)视图 侧(左)视图 俯视图图图 ‎10．先后抛掷两枚均匀的正方体骰子（它们的六个面分别标有点数1、2、3、4、5、6），骰子朝上的面的点数分别为，则函数在区间上是减函数的概率为（ ）‎ A． B. C． D． ‎ ‎11. 如右图，已知一个锥体的正（主）视图，侧（左）视图和俯视图均 为直角三角形，且面积分别为、、，则该锥体的体积为（ ）‎ A． B． C． D．‎ ‎12．计算机是将信息转换成二进制进行处理的. 二进制即“逢二进一”，如表示二进制数，将它转换成十进制形式是= 13，那么将二进制数转换成十进制形式是（ ）‎ A. B. C. D.‎ 二、填空题：本大题共4小题，每小题5分，满分20分，请将答案填在答题卡相应位置.‎ ‎13．函数的定义域为_____________________.‎ ‎14．已知，则_______________‎ ‎15．已知直线过圆的圆心，则的最小值为________________‎ ‎16．第26届世界大学生夏季运动会将于 ‎2011年8月12日至23日在深圳举行，下表是组委会对其中 一位运动员的心脏跳动检测了8次的数据：‎ 检测次数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 检测数据（次/分钟）‎ ‎39‎ ‎40‎ ‎42‎ ‎42‎ ‎43‎ ‎45‎ ‎46‎ ‎47‎ 上述数据的统计分析中，一部分计算见如右图所示的程序框图 ‎（其中是这8个数据的平均数），则输出的的值是________‎ 三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．‎ ‎17.（本题满分10分）‎ 已知△的内角所对的边分别为且.‎ ‎（1）若, 求的值; ‎ ‎（2）若△的面积 求的值.‎ ‎ ‎ ‎18.（本题满分12分）‎ 已知：命题P：函数在上单调递增，‎ 命题Q：关于的不等式的解集为R，‎ 若“PQ”为真命题，“”为假命题，求的实数m的取值范围。‎ ‎ ‎ ‎19.（本题满分12分）‎ 已知数列满足，． ‎ ‎（1）求证：数列是等比数列；‎ ‎（2）求数列的通项公式和前项和 ‎20.（本题满分12分）‎ 某班级新年晚会上有一个猜数游戏,让参加游戏的两名同学分别从区间[0，3]中选取一个数，设为x和y，若x和y满足关系式，就称这两人“心灵相通”。‎ ‎（1）若规定，求参加游戏的两名同学“心灵相通”的概率；‎ ‎（2）若规定，求参加游戏的两名同学“心灵相通”的概率 ‎21.（本题满分12分）‎ 如图4，是圆柱的母线，是圆柱底面圆的直径，‎ 是底面圆周上异于的任意一点， ．‎ ‎（1）求证：⊥平面；‎ ‎（2）求三棱锥的体积的最大值．‎ ‎ ‎ ‎22.（本题满分12分）‎ 已知圆：，直线：，且与相交于、两点，点，且.‎ ‎（1）当时，求的值； ‎ ‎（2）当，求的取值范围.‎ 惠阳高级中学实验中学2019届高二第一学期 期中考试理科数学试题 参考答案 ‎ 一、选择题（每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D B B C D B A C C A D C 二、填空题：（每小题5分，共20分）‎ ‎13、 ， 14、 ‎ ‎ 15、 9 ， 16、 7 ‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎17．（本小题满分10分） ‎ 解：解: (1)∵, 且, ‎ ‎∴ . …………………………………………2分 ‎ ‎ 由正弦定理得，‎ ‎∴. …………………………………………5分 ‎ ‎ (2)∵ ‎ ‎∴， ∴ . …………………………………………7分 ‎ ‎ 由余弦定理得，‎ ‎∴ ………10分 ‎ ‎18. （本小题满分12分） ‎ 解：解：函数的对称轴为 故P为真时，……………………………………………………………2分 ‎ ‎ Q为真时， ………………4分 ‎∵“PQ”为真命题，为假命题 ‎∴P与Q一真一假。……………………………………………………………6分 ‎ 若P真Q假，则且或，∴………………………8分 ‎ 若P假Q真，则且，∴………………………10分 ‎ 综上，实数m的取值范围是或 ……………………12分 ‎ ‎ ‎ ‎19．（本小题满分12分） ‎ 解：(1)依题意有 ‎ 所以, ………………………………………………………………3分 又， ………………………………………………………………4分 所以数列是以2为首项一为公比的等比数列 ……………………6分 ‎ ‎ ‎(2)由(1)知,‎ ‎， ……………………………………………………8分 ‎ ‎ ‎…………………………………………………10分 ‎ ………………………………………………………………12分 ‎20．（本小题满分12分） ‎ 证明： 解：在平面直角坐标系内, 设,设以(x,y)为坐标的点是P, 若两名同学“心灵相通”，则等价于点P(x,y)在区域M内。‎ ‎（1）若，且，则满足条件x∈{0,1,2,3}‎ 且y∈{0,1,2,3}的点P(x,y)共有16个，而其中满足关系式的点只有10个，如图。‎ 所以，此时两名同学“心灵相通”的概率为。 （列表法，也不错）‎ ‎ （2）若，且，则满足条件 且 的点P(x,y)的集合是，‎ 而其中满足关系式的点都落在集合M内，如图。‎ 所以，此时两名同学“心灵相通”的概率为。‎ ‎21．（本小题满分12分） ‎ ‎ 解：（1）证明：∵是底面圆周上异于、的一点，且为底面圆的直径，‎ ‎∴， ……………………………………………………2分 ‎ ‎∵⊥平面，平面，‎ ‎∴， ……………………………………………………4分 ‎ ‎∵平面,平面,‎ ‎∴平面． ……………………………………………………6分 ‎ ‎ （2） 在Rt△ 中，, ‎ ‎ ‎ ‎ ………………………………………10分 ‎ ‎ 当且仅当时等号成立，此时.‎ ‎ ∴三棱锥的体积的最大值为. ……………………………………12分 ‎ ‎22.（本小题满分12分） ‎ 解：解:（1）圆：,当时，点在圆上,‎ 当且仅当直线经过圆心时, 满足. ‎ 圆心的坐标为,. ………………………………………4分 ‎ ‎（2）由消去得:. ①……6分 ‎ 设,. ‎ ‎,.‎ ‎, 即.‎ ‎,‎ ‎, 即 . ‎ ‎ ,即.…………8分 ‎ 令, 则.‎ 当时, >0.‎ 在区间上单调递增.‎ ‎ 当时,. ‎ ‎ .即解得 或. ……………………………10分 ‎ 由①式得, 解得.‎ 或.的取值范围是. ‎ ‎………………………………………12分 ‎