上海市黄浦区2013届高三下学期二模数学（文）试题

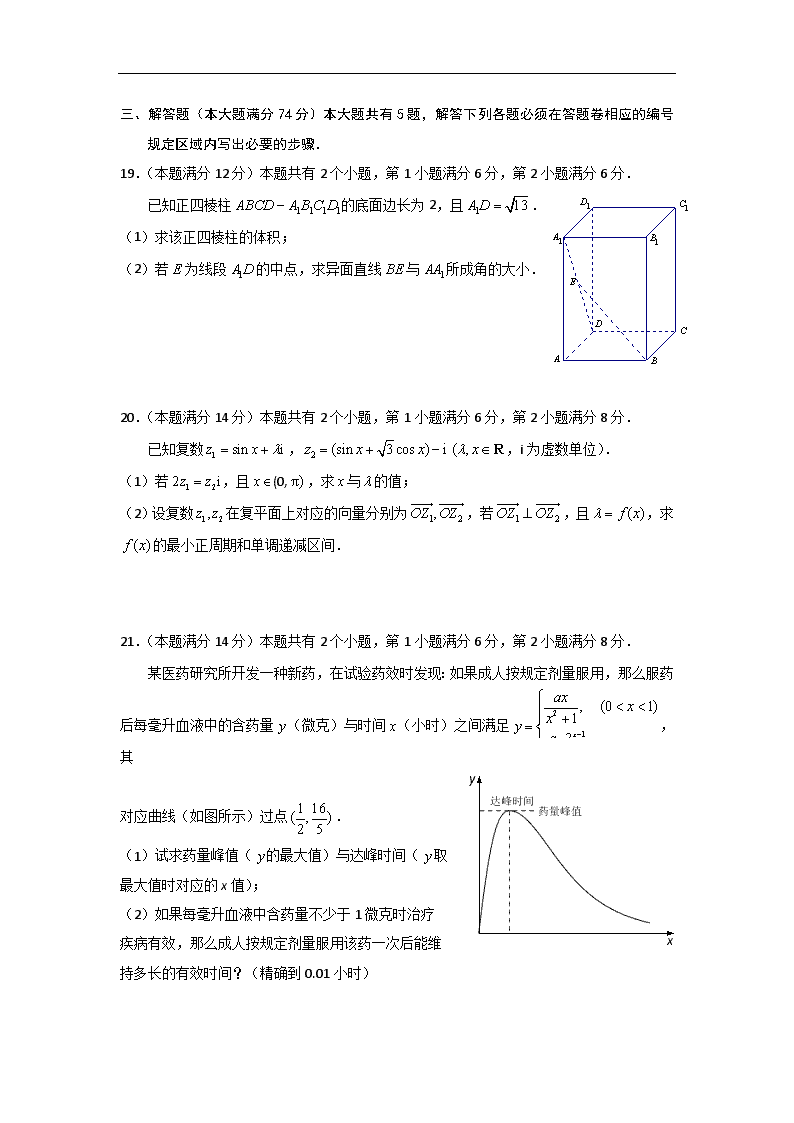
上海市黄浦区2013届高三下学期二模数学（文）试题

黄浦区2013年高考模拟考 ‎ 数学试卷(文科) ‎‎2013年4月11日 考生注意：‎ ‎1．每位考生应同时收到试卷和答题卷两份材料，解答必须在答题卷上进行，写在试卷上的解答一律无效；‎ ‎2．答卷前，考生务必将姓名、准考证号等相关信息在答题卷上填写清楚；‎ ‎3．本试卷共23道试题，满分150分；考试时间120分钟．‎ 一、填空题(本大题满分56分)　本大题共有14题，考生应在答题卷的相应编号的空格内直 接填写结果，每题填对得4分，否则一律得零分．‎ ‎1．函数的定义域为　　　　　．‎ 结束 否 开始 ‎ a←1‎ a←‎3a+1‎ 输出a a >100‎ 是 ‎ ‎（第7题图）‎ ‎2．若复数满足，则的值为　　　　　．‎ ‎3．在正△中，若，则　　　　　．‎ ‎4．若直线过点，且与直线垂直，则直线 的方程为　　　　　．‎ ‎5．等差数列的前10项和为，则　 ．　　　　　　　　　　　 　　‎ ‎6．设a为常数，函数．若在上是 增函数，则的取值范围是 　 ．‎ ‎7．执行右边的程序框图，则输出的a值是 ． ‎ ‎8．已知点的坐标满足 点为坐标原点，则 的最小值为　　　 　．‎ ‎9．已知点是双曲线上一点，双曲线两个焦点间的距离等于4，‎ 则该双曲线方程是 ．‎ ‎10．已知圆是球的小圆，若圆的半径为cm，球心到圆所在平面的距离为 cm，则球的表面积为 　 cm2．‎ ‎11．在△中，，，，则的值为　　　　　．‎ ‎12．已知，且 ‎，则 ．‎ ‎13．一厂家向用户提供的一箱产品共10件，其中有2件次品．用户随机抽取3件产品进行检 验，若这3件产品中至少有一件次品，就拒收这箱产品；若这3件产品中没有次品，就接收 这箱产品．那么这箱产品被用户拒收的概率是　　　　　．（用数字作答）‎ ‎14．已知，若存在区间，使得，‎ 则实数的取值范围是 ．‎ ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u ks5u 二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题卷的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．‎ ‎15．已知，且，则的值为　　　　　　　　 （　 ）‎ A． B．　　 C． 　 D． ‎ ‎16．函数的反函数是　 　 （ 　）‎ A． B． ‎ C． D． ‎ ‎17．如果函数y的图像与曲线恰好有两个不同的公共点，则实数的取 值范围是 　　 　 （ ）‎ A．∪ 　 B． C． 　 D．　 　‎ ‎18．下列命题：①“”是“存在，使得成立”的充分条件；②“”‎ 是“存在，使得成立”的必要条件；③“”是“不等式对一切 恒成立”的充要条件．其中所有真命题的序号是　 　 　　 　 　 （　 ）‎ A．③ B．②③ C．①② D．①③ ‎ 三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题卷相应的编号规定区域内写出必要的步骤．‎ ‎19．（本题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分．‎ 已知正四棱柱的底面边长为2，且．‎ ‎（1）求该正四棱柱的体积；‎ ‎（2）若为线段的中点，求异面直线与所成角的大小．‎ ‎20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ 已知复数，，i为虚数单位）．‎ ‎（1）若，且(0,，求与的值；‎ ‎（2）设复数在复平面上对应的向量分别为，若，且，求 的最小正周期和单调递减区间．‎ ‎21．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ 某医药研究所开发一种新药，在试验药效时发现：如果成人按规定剂量服用，那么服药 y x 后每毫升血液中的含药量（微克）与时间（小时）之间满足，其 对应曲线（如图所示）过点．‎ ‎（1）试求药量峰值（的最大值）与达峰时间（取 最大值时对应的x值）；‎ ‎（2）如果每毫升血液中含药量不少于1微克时治疗 疾病有效，那么成人按规定剂量服用该药一次后能维 持多长的有效时间？（精确到0.01小时）‎ ‎22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分．‎ 设抛物线的焦点为，经过点的动直线交抛物线于 两点，且．‎ ‎（1）求抛物线的方程； ‎ ‎（2）若直线平分线段，求直线的倾斜角．‎ ‎（3）若点是抛物线的准线上的一点，直线的斜率分别为．求证：当时，为定值．‎ ‎23．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．‎ 已知数列具有性质：①为整数；②对于任意的正整数n，当为偶数时，；‎ 当为奇数时，．‎ ‎（1）若，求数列的通项公式；‎ ‎（2）若成等差数列，求的值；‎ ‎（3）设（且N），数列的前n项和为，求证：．‎ 黄浦区2013年高考模拟考数学试卷 ‎（文科）参考答案和评分标准 说明：‎ ‎1．本解答仅列出试题的一种或两种解法，如果考生的解法与所列解答不同，可参考解答中的评分精神进行评分．‎ ‎2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误，影响了后继部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，这时原则上不应超过后面部分应给分数之半，如果有较严重的概念性错误，就不给分．‎ 一、填空题（本大题满分56分）本大题共有14小题，考生应在答题卷相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．‎ ‎1．； 2．；　　3．2； 　4．； 　5．12；　 　6．； ‎ ‎7．121；　　 8．；　9．；　10．；　11．；　 12．；‎ ‎13．； 　14．． ‎ 二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题卷的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．‎ ‎15．C 16．D 17．A 18． B 三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题卷相应的编号规定区域内写出必要的步骤．‎ ‎19．（本题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分．‎ 解：解：（1）在正四棱柱中，‎ ‎∵平面，平面，‎ ‎∴，故，………………3分 ‎∴正四棱柱的体积为． ………………6分 ‎（2）设是棱中点，连，在△中，‎ ‎∵分别为线段的中点，‎ ‎∴∥，且，‎ ‎∴就是异面直线与所成的角． ……8分 ‎∵平面ABCD，平面，∴，‎ 又∥，∴， ……………………10分 ‎∵，‎ ‎∴，故．‎ 所以异面直线与所成角的大小为． …………………………12分 ‎20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ 解：（1）由，可得，又，‎ ‎∴又，　　 　 …………………………2分 故或　　 　　　　　　　　　　 　………………………6分 ‎（2），‎ 由，可得，　　　　 　………………………8分 又，故 ‎　　　　　　　　　…………………………11分 故的最小正周期， …………………………12分 又由Z），可得，‎ 故的单调递减区间为． …………………………14分 ‎ ‎21．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ 解：（1）由曲线过点，可得，故　　 　……………………2分 当时，， ……………………3分 当时，设，可知，‎ ‎（当且仅当时，） ……………………5分 综上可知，且当取最大值时，对应的值为1‎ 所以药量峰值为4mg，达峰时间为1小时． ……………………6分 ‎（2）当时，由，可得，‎ 解得，又，故． ……………………8分 当时，设，则，‎ 由，可得，解得，‎ 又，故，所以，‎ 可得．　　　　　　　　 …………………………………………12分 由图像知当时，对应的的取值范围是，‎ ‎∵，‎ 所以成人按规定剂量服用该药一次后能维持大约小时的有效时间． …………14分 ‎【另法提示：可直接解不等式，得出x的取值范围，然后求出有效时间】‎ ‎22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分．‎ 解：（1）设直线的方程为，代入，可得 ‎　　　　　 （*）‎ 由是直线与抛物线的两交点，‎ 故是方程（*）的两个实根， ……………………2分 ‎∴，又，所以，又，可得 所以抛物线的方程为．　　　　　　　　　　　　　　……………………4分 ‎【另法提示：考虑直线l垂直于x轴这一特殊情形，或设直线l方程为点斜式】‎ ‎（2）由（1）可知，‎ 设点是线段的中点，则有 ‎，， ………………………7分 ‎ 由题意知点在直线上，‎ ‎∴，解得或，‎ 设直线的倾斜角为，则或，又，‎ 故直线的倾斜角为或．　　　　 　 ………………………10分 ‎【另法提示：设直线l方程为点斜式】‎ ‎（3），可得， ………………………11分 由（2）知又，‎ ‎∴　 ‎ ‎　　　 ………………………14分 ‎　　　，‎ 所以为定值．　　　　　　　　　　　 ………………………16分 ‎【另法提示：分直线l斜率存在与不存在两种情形讨论，斜率存在时设直线l方程为点斜式】‎ ‎23．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．‎ ‎（1）由，可得，，…，，，，，…， ‎ ‎ 即的前7项成等比数列，从第8起数列的项均为0．　　 ……………………2分 故数列的通项公式为．　 …………………4分 ‎（2）若时，，，‎ 由成等差数列，可知即，解得，故； ‎ 若时，，，‎ 由成等差数列，可知，解得，故；………7分 ‎ 若时，，，‎ 由成等差数列，可知，解得，故；‎ 若时，，，‎ 由成等差数列，可知，解得，故；‎ ‎∴的值为． 　 ……………………10分 ‎（3）由（），可得， ‎ ‎，，‎ 若，则是奇数，从而，‎ 可得当时，成立． ……………………13分 又，，…‎ 故当时，；当时，． ……………………15分 故对于给定的，的最大值为 ‎，‎ 故． ……………………18分