2019学年高中数学暑假作业 第三部分 概率 3古典概型与几何概型

2019学年高中数学暑假作业 第三部分 概率 3古典概型与几何概型

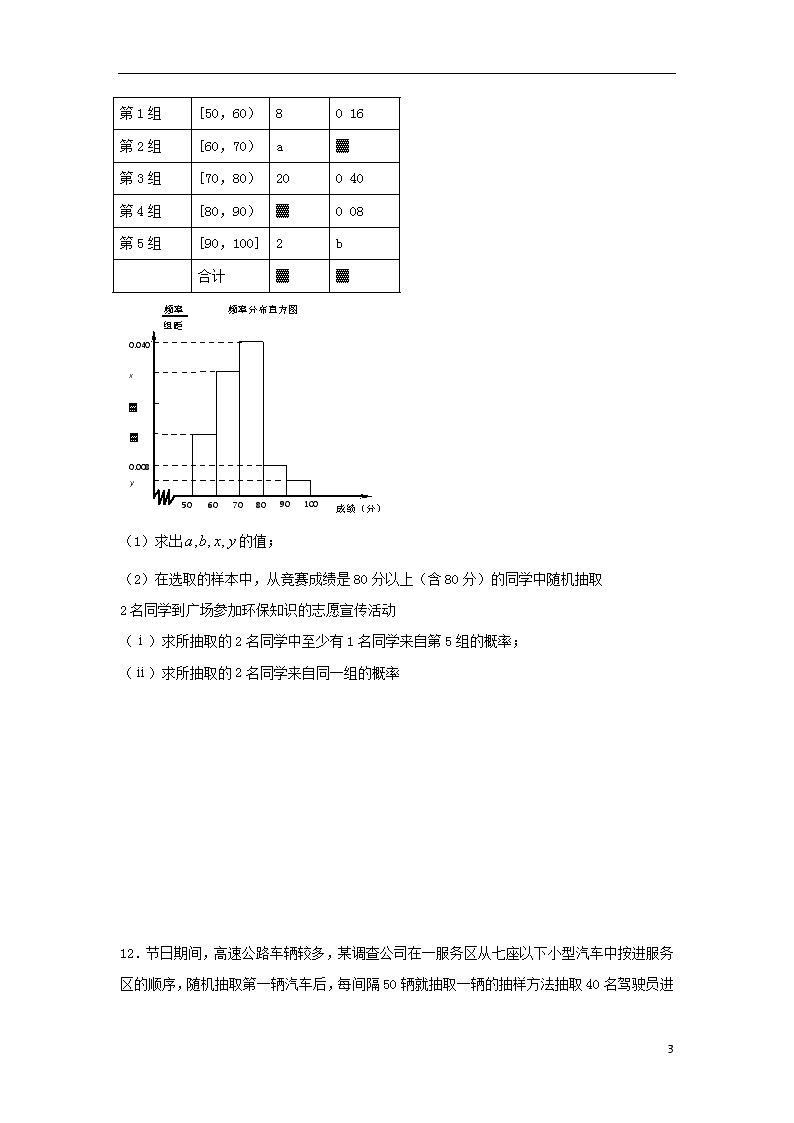
‎3.2古典概型与几何概型 典型例题：‎ ‎1．现有名女教师和名男教师参加说题比赛，共有道备选题目，若每位选手从中有放回地随机选出一道题进行说题，其中恰有一男一女抽到同一道题的概率为（ ）‎ A. B. C. D. ‎ ‎2．在区间上随机选取两个数和，则的概率为（ ）‎ A. B． C． D．‎ ‎3．在区间上随机选取一个数，若的概率为，则实数的值为（ ）‎ A．2 B．‎3 C．4 D．5‎ 巩固练习：‎ ‎1．某校3名教师和3名学生共6人去北京参加学习方法研讨会，须乘坐两辆车，每车坐人，则恰有两名教师在同一车上的概率（ ）‎ A． B． C． D．‎ ‎2．从集合中随机选取一个数记为，从集合中随机选取一个数记为，则直线不经过第四象限的概率为（ ）‎ A． B． C． D．‎ ‎3．已知函数，若在区间内随机取一个数，则的概率为 （ ）‎ A． B． C. D．‎ ‎4．在区间中随机取出两个数，则两数之和不小于的概率是（ ）‎ A. B. C. D.‎ ‎5．如图圆内切于扇形，，若在扇形内任取一点，则该点在圆 9‎ 内的概率为（ ）‎ A． B． ‎ C． D．‎ ‎6．若某公司从5位大学毕业生甲、乙、丙、丁、戌中录用3人，这5人被录用的机会均等，则甲或乙被录用的概率为（ ）‎ A． B． C． D．‎ ‎7．取一个正方形及其它的外接圆，随机向圆内抛一粒豆子，则豆子落入正方形外的概率为（ ）‎ A． B． C． D．‎ ‎8．在底面半径为1，高为2的圆柱内随机取一点到圆柱底面圆心的距离大于1的概率为（ ）‎ A． B． C． D．‎ ‎9．从内任意取两个实数，这两个数的平方和小于1的概率为 . ‎ ‎10．已知圆M：，在圆M上随机取两点A、B，使的概率为 .‎ ‎11．某中学举行了一次“环保知识竞赛”， 全校学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示）解决下列问题：‎ 频率分布表 组别 分组 频数 频率 9‎ 第1组 ‎[50，60）‎ ‎8‎ ‎0 16‎ 第2组 ‎[60，70）‎ a ‎▓‎ 第3组 ‎[70，80）‎ ‎20‎ ‎0 40‎ 第4组 ‎[80，90）‎ ‎▓‎ ‎0 08‎ 第5组 ‎[90，100]‎ ‎2‎ b 合计 ‎▓‎ ‎▓‎ 组距 频率 成绩（分）‎ 频率分布直方图 ‎0.040‎ x ‎▓‎ ‎0.008‎ ‎▓‎ ‎50‎ ‎60‎ ‎80‎ ‎70‎ ‎90‎ ‎100‎ y ‎（1）求出的值；‎ ‎（2）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取 ‎2名同学到广场参加环保知识的志愿宣传活动 ‎ ‎（ⅰ）求所抽取的2名同学中至少有1名同学来自第5组的概率；‎ ‎（ⅱ）求所抽取的2名同学来自同一组的概率 ‎12．节日期间，高速公路车辆较多，某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序，随机抽取第一辆汽车后，‎ 9‎ 每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（）分成六段，，，，，后得到如下图的频率分布直方图．‎ ‎（1）请直接回答这种抽样方法是什么抽样方法？并估计出这40辆车速的中位数；‎ ‎（2）设车速在的车辆为，， ，（为车速在上的频数），车速在的车辆为，， ，（为车速在上的频数），从车速在的车辆中任意抽取辆共有几种情况？请列举出所有的情况，并求抽取的辆车的车速都在上的概率．‎ 9‎ ‎3.2古典概型与几何概型 典型例题：‎ ‎1. C【解析】‎ 试题分析：设两道题分别为A，B题，所以抽取情况共有：AAA，AAB，ABA，ABB，BAA，BAB，BBA，BBB，其中第1个，第2个分别是两个女教师抽取的题目，第3个表示男教师抽取的题目，一共有8种；其中满足恰有一男一女抽到同一题目的事件有：ABA，ABB，BAA，BAB，共4种；‎ 故所求事件的概率为 ‎2. A【解析】试题分析：的概率为.选A.‎ ‎3. C【解析】试题分析：由得．选C．‎ 巩固练习：‎ ‎1. C ‎2. A【解析】试题分析：集合中各有三个元素，随机选取，所有可能有种，直线是不经过第四象限时，且，满足条件的有两种，则直线是不经过第四象限的概率为 ‎3. D【解析】试题分析：在同一坐标系中作出函数与，如图所示，则由图可知，两个函数的图象交点为，则在内时，，所以的概率为，故选D．‎ ‎4. D【解析】‎ 9‎ 试题分析：设取出两个数为；则，若这两数之和小于，则有，根据几何概型，原问题可以转化为求不等式组；表示的区域与表示区域的面积之比问题，如图所示；易得其概率为 .‎ 考点：几何概型.‎ ‎5. C ‎【解析】‎ 试题分析：作辅助线，则设圆的半径为，可得所以扇形的半径为，由几何概型，点在圆内的概率为，故选C.‎ 9‎ ‎6. D ‎7. B【解析】试题分析：设圆的半径为，所以正方形边长为，正方形面积为，圆的面积为 ‎8. B【解析】试题分析:因到底面圆心的距离为的点的轨迹是半径为的球,其体积,而圆柱的体积,故满足题设条件的概率是,选B.‎ ‎9. ‎ ‎10. 试题分析：设，当时，取线段的中点，则，在中，，故，即，故的概率为．‎ ‎11. 【答案】（1）．（2）（ⅰ）．（ⅱ）‎ ‎【解析】（1）由题意可知，． （4分）‎ ‎（2）（ⅰ）由题意可知，第4组共有4人，记为，第5组共有2人，记为．‎ 从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学有，‎ 9‎ 共15种情况． （6分）‎ 设“随机抽取的2名同学中至少有1名同学来自第5组”为事件， ‎ 有，共9种情况． （9分）‎ 所以随机抽取的2名同学中至少有1名同学来自第5组的概率是． （10分）‎ ‎（ⅱ）设“随机抽取的2名同学来自同一组”为事件，有共7种情况．‎ 所以随机抽取的2名同学来自同一组的概率 （12分）‎ ‎12. 【答案】（1）系统抽样，；（2）‎ ‎【解析】试题分析：（1）系统抽样的方法是每间隔一个相同的长度，抽取一个样本.所以本小题符合系统抽样的方法.通过直方图计算中位数，是指直方图中从左到右直方图的面积为二分之一这条分界线所对的值，通过运算可求得中位数的估算值.‎ ‎（2）由于车速在的车辆频率为0.05，车速在的车辆的频率为0.1.所以可求出车速在这两段上的车辆数.再求出相应的概率即可.‎ ‎（1）此调查公司在抽样中，用到的抽样方法是系统抽样． 2分 ‎ ‎∵车速在区间，，，上的频率分别为，，，；‎ ‎∴车速在区间上的频率是，车速在区间上的频率是．‎ ‎∴中位数在区间内． 2分 设中位数的估计值是，‎ ‎∴．‎ 解之得．‎ ‎∴中位数的估计值为 6分 ‎ ‎（2）由（1）得，． 8分 ‎∴所以车速在的车辆中任意抽取辆的所有情况是：‎ 9‎ ‎，共有种情况． 10分 车速都在上的辆车的情况有种．所以车速都在上的辆车的概率是． 12分 考点：1.统 9‎