辽宁省沈阳市2019届高三一模理科数学答案

辽宁省沈阳市2019届高三一模理科数学答案

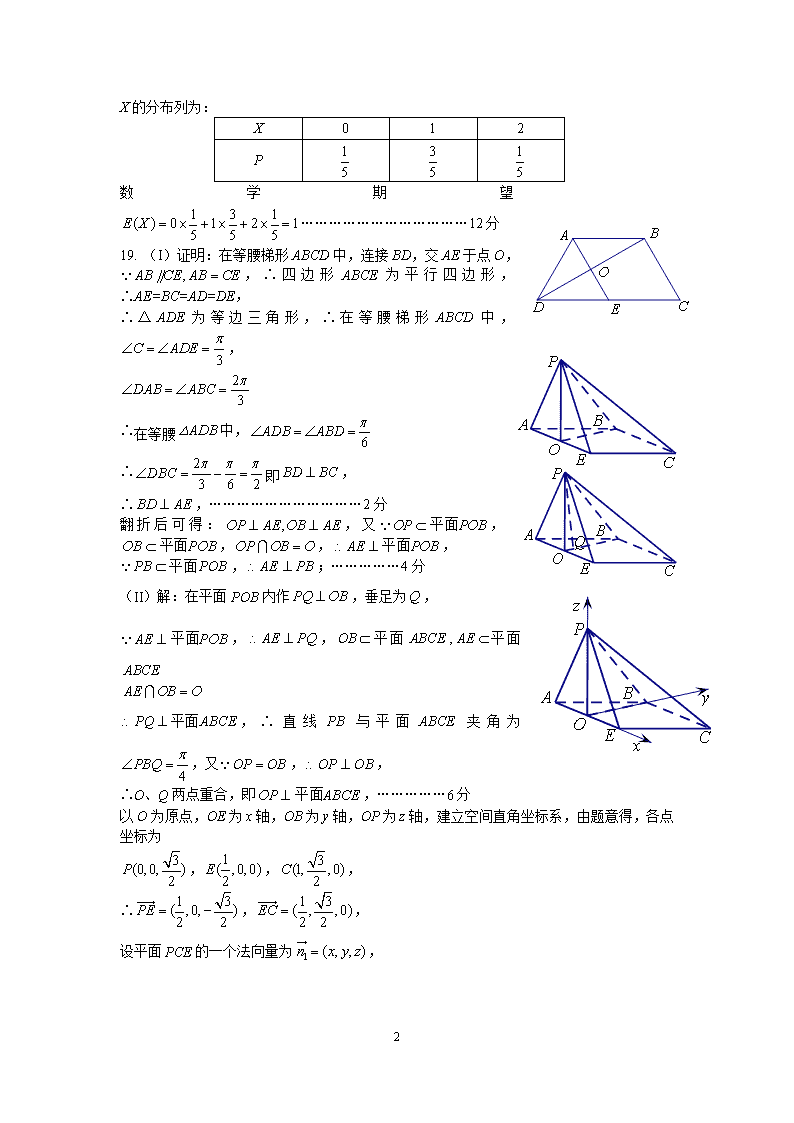
‎2019年沈阳市高三第二次模拟考试数学（理科）‎ 参考答案与评分标准 一、选择题DAABC BDADB DC 二、填空题13. 8 14. 15. 16.‎ 三、解答题 ‎17.解：（Ⅰ）由正弦定理得：所以，，……3分 所以，所以……………6分 ‎（Ⅱ）设，则，所以 解得：所以………………………12分 ‎18. 解：（I）估计第一车间生产时间小于75min的工人人数为 ‎（人）…………………………………………………2分 估计第二车间生产时间小于75min的工人人数为 ‎（人）………………………………4分 ‎（II）第一车间生产时间平均值约为 ‎（min）……………………5分 第二车间生产时间平均值约为 ‎（min）………6分 ‎∵，∴第二车间工人生产效率更高………………………8分 ‎（III）由题意得，第一车间被统计的生产时间小于75min的工人有6人，其中生产时间小于65min的有2人，从中抽取3人，随机变量X服从超几何分布，‎ X可取值为0，1，2，‎ ‎，………………………………………………9分 ‎，……………………………………………10分 ‎………………………………………………11分 9‎ X的分布列为：‎ X ‎0‎ ‎1‎ ‎2‎ P 数学期望………………………………12分 ‎19. （I）证明：在等腰梯形ABCD中，连接BD，交AE于点O，‎ ‎，∴四边形ABCE为平行四边形，∴AE=BC=AD=DE，‎ ‎∴△ADE为等边三角形，∴在等腰梯形ABCD中，，‎ ‎∴在等腰中，‎ ‎∴即，‎ ‎∴，……………………………2分 翻折后可得：，又，，，，‎ ‎，；……………4分 ‎（II）解：在平面POB内作，垂足为，‎ ‎，，平面,平面 ‎，∴直线PB与平面ABCE夹角为，又，，‎ ‎∴O、Q两点重合，即，……………6分 以O为原点，OE为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，由题意得，各点坐标为 ‎，，，‎ ‎∴，，‎ 设平面PCE的一个法向量为，‎ 9‎ 则，即，设，则，，‎ ‎∴，…………………………………………………………8分 由题意得平面PAE的一个法向量，………………………9分 设二面角A-EP-C为，…………11分 易知二面角A-EP-C为钝角，所以………………………12分 ‎20．解：（I）法一：设，，，，‎ 直线：①………………………………1分 直线：②………………………………2分 得，又，‎ ‎，‎ 整理得点N的轨迹方程为：（）……………………6分 法二：设，，，，‎ 直线：……①‎ 直线：……②‎ 9‎ 由①，②解得：，又，‎ ‎，……………………………………………………………4分 故，代入得：，‎ 点N的轨迹方程为（）…………………………6分 法三：设直线：，则直线：①‎ 直线与椭圆C：的交点M的坐标为 ‎，……………………………………………………2分 则直线的斜率为，‎ 直线：……②‎ 由①，②解得N点的坐标为，………………4分 由解得：‎ 点N的轨迹方程为：（）…………………………6分 ‎（II）法一：设，，由（I）法二得：‎ 四边形的面积，……10分 9‎ ‎，当时，的最大值为.……………12分 法二：由（I）法三得：四边形的面积 ‎……………………………………………………………………………10分 当且仅当时，取得最大值.…………………………12分 ‎21.解：（Ⅰ）， ∵‎ ‎∴①当时，在上恒成立，‎ ‎∴在上单调递减，无单调递增区间；…………………1分 ‎②当，且，即时，在上恒成立，‎ ‎∴在上单调递减，无单调递增区间；………………2分 ‎③当，且，即时，在上，，在上，，∴在上单调递减，上单调递增 ……3分 综上，当时，在上单调递减，无单调递增区间；‎ 当时，在上单调递减，上单调递增……4分 ‎（Ⅱ）∵是的极值点， ∴由（1）可知， ∴‎ 设曲线在处的切线方程为，‎ 曲线在处的切线方程为 ‎∴若这两条切线互相平行，则,∴‎ ‎∵,且，∴，∴，‎ 9‎ ‎∴…………………………………………………………………5分 两条切线在轴上的截距：‎ 令，则，同理，………………7分 法一：∵，‎ ‎∴‎ 设，…………………………9分 ‎∴‎ ‎∴在区间上单调递减，……………………………………10分 ‎∴‎ 即的取值范围是.……………………………………12分 法二：∵，‎ ‎∴‎ 令，其中………………………………9分 ‎∴‎ ‎∴函数在区间上单调递增，…………………………………10分 ‎∴‎ ‎∴的取值范围是.…………………………………12分 法三：∵，‎ 9‎ ‎∴‎ 设∵，‎ ‎…………………………………………………………………9分 ‎∴，∴函数在区间上单调递增， ………………10分 ‎∴‎ ‎∴的取值范围是.……………………………………12分 ‎22.解：（Ⅰ）直线的参数方程为，‎ 即（为参数）………………………………………2分 设,‎ ‎,即，即，‎ 所以.……………………………………………5分 ‎（Ⅱ）将的参数方程代入的直角坐标方程中，‎ ‎……………………………7分 即,为方程的两个根，所以，………………9分 9‎ 所以.…………………………………………10分 ‎23.解：（Ⅰ）①当时，……1分 ‎②当时，………………2分 ‎③当时，………………3分 综上：的解集为……………………………5分 ‎（II）：由（I）可知，即……6分 又且，则，设，，，，，‎ 同理：，，‎ ‎，……8分 ‎，‎ ‎，即，……9分 当且仅当时，取得最大值.……………………10分 法：由（I）可知，‎ 即…………………………………………6分 ‎，…………7分 由柯西不等式可知 即………………………………9分 当且仅当，‎ 9‎ 即时，取得最大值.………………………………10分 9‎