高考数学专题复习课件：4-3正弦函数、余弦函数、正切函数的图象与性质

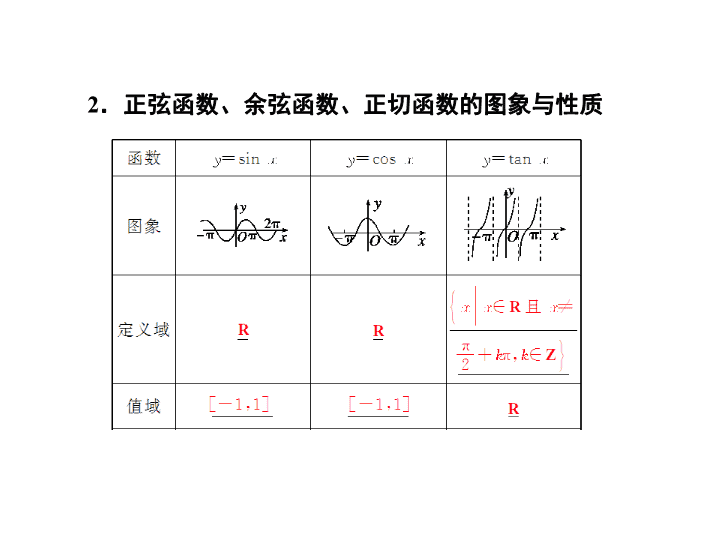
高考数学专题复习课件：4-3正弦函数、余弦函数、正切函数的图象与性质

2 ．正弦函数、余弦函数、正切函数的图象与性质 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) y ＝ sin x 在第一、第四象限是增函数． ( 　　 ) (2) 常数函数 f ( x ) ＝ a 是周期函数，它没有最小正周期． ( 　　 ) (3) 正切函数 y ＝ tan x 在定义域内是增函数． ( 　　 ) 【 答案 】 (1) × 　 (2) √ 　 (3) × 　 (4) × 　 (5) √ 　 (6) × 【 答案 】 B 【 答案 】 D 【 答案 】 B 【 答案 】 A 【 答案 】 A 【 方法规律 】 (1) 三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式 ( 组 ) ，常借助三角函数线或三角函数图象来求解． (2) 三角函数值域的不同求法 ① 利用 sin x 和 cos x 的值域直接求； ② 把所给的三角函数式变换成 y ＝ A sin( ωx ＋ φ ) 的形式求值域； ③ 通过换元，转换成二次函数求值域． 【 方法规律 】 (1) 已知三角函数解析式求单调区间： ① 求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性规律 “ 同增异减 ” ； ② 求形如 y ＝ A sin( ωx ＋ φ ) 或 y ＝ A cos( ωx ＋ φ )( 其中 ω ＞ 0) 的单调区间时，要视 “ ωx ＋ φ ” 为一个整体，通过解不等式求解．但如果 ω ＜ 0 ，那么一定先借助诱导公式将 ω 化为正数，防止把单调性弄错． (2) 已知三角函数的单调区间求参数．先求出函数的单调区间，然后利用集合间的关系求解． 【 答案 】 A 【 答案 】 B 【 方法规律 】 (1) 对于函数 y ＝ A sin( ωx ＋ φ ) ，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线 x ＝ x 0 或点 ( x 0 ， 0) 是不是函数的对称轴或对称中心时，可通过检验 f ( x 0 ) 的值进行判断． (2) 求三角函数周期的方法： ① 利用周期函数的定义． 【 答案 】 (1)2 或－ 2 　 (2)D (2) (2015· 课标全国 Ⅰ ) 函数 f ( x ) ＝ cos( ωx ＋ φ ) 的部分图象如图所示，则 f ( x ) 的单调递减区间为 ( 　　 ) 【 思维点拨 】 (1) 逐个验证所给函数是否满足条件； (2) 根据图象先确定函数的周期性，然后先在一个周期内确定 f ( x ) 的减区间； (3) 由零点可得函数的对称轴，应用函数在对称轴处的性质求解即可． 【 答案 】 (1)A 　 (2)D 　 (3)B 【 温馨提醒 】 (1) 研究三角函数的性质时一定要做到心中有图，充分利用数形结合思想； (2) 函数 y ＝ A sin( ωx ＋ φ ) 的图象与对称轴的交点是最值点 . 3 ．对于函数的性质 ( 定义域、值域、单调性、对称性、最值等 ) 可以通过换元的方法令 t ＝ ωx ＋ φ ，将其转化为研究 y ＝ sin t 的性质． 4 ．对于已知函数的单调区间的某一部分确定参数 ω 的范围的问题：首先，明确已知的单调区间应为函数的单调区间的子集；其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解． ► 失误与防范 1 ．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响． 2 ．要注意求函数 y ＝ A sin( ωx ＋ φ ) 的单调区间时 ω 的符号，若 ω ＜ 0 ，那么一定先借助诱导公式将 ω 化为正数． 3 ．三角函数的最值可能不在自变量区间的端点处取得，直接将两个端点处的函数值作为最值是错误的 .