【数学】2018届一轮复习北师大版函数y＝Asin（ωx＋φ）的图象学案

【数学】2018届一轮复习北师大版函数y＝Asin（ωx＋φ）的图象学案

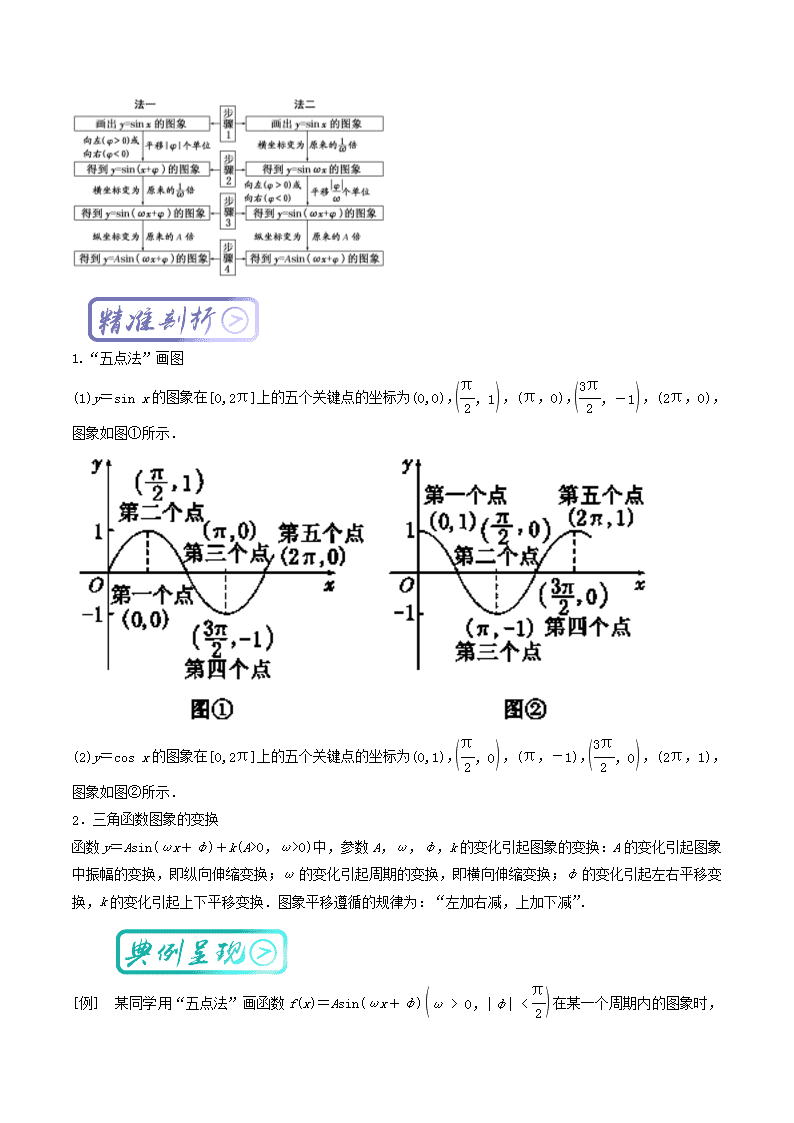
专题8 函数y＝Asin(ωx＋φ)的图象 函数y＝Asin(ωx＋φ)的图象 ‎★★★‎ ‎○○○○‎ ‎1．y＝Asin(ωx＋φ)的有关概念 y＝Asin(ωx＋φ) (A>0，ω>0)‎ 振幅 周期 频率 相位 初相 A T＝ f＝＝ ωx＋φ φ ‎2.用五点法画y＝Asin(ωx＋φ)一个周期内的简图 用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示：‎ x ‎－ ‎－＋ － ωx＋φ ‎0‎ π ‎2π y＝Asin(ωx＋φ)‎ ‎0‎ A ‎0‎ ‎－A ‎0‎ ‎3.由函数y＝sin x的图象变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种方法 ‎1.“五点法”画图 ‎(1)y＝sin x的图象在[0,2π]上的五个关键点的坐标为(0,0)，，(π，0)，，(2π，0)，图象如图①所示．‎ ‎(2)y＝cos x的图象在[0,2π]上的五个关键点的坐标为(0,1)，，(π，－1)，，(2π，1)，图象如图②所示．‎ ‎2．三角函数图象的变换 函数y＝Asin(ωx＋φ)＋k(A>0，ω>0)中，参数A，ω，φ，k的变化引起图象的变换：A的变化引起图象中振幅的变换，即纵向伸缩变换；ω的变化引起周期的变换，即横向伸缩变换；φ的变化引起左右平移变换，k的变化引起上下平移变换．图象平移遵循的规律为：“左加右减，上加下减”．‎ ‎[例]　某同学用“五点法”画函数f(x)＝Asin(ωx＋φ) 在某一个周期内的图象时，列表并填入了部分数据，如下表：‎ ωx＋φ ‎0‎ π ‎2π x Asin(ωx＋φ)‎ ‎0‎ ‎5‎ ‎－5‎ ‎0‎ ‎(1)请将上表数据补充完整，并直接写出函数f(x)的解析式；‎ ‎(2)将y＝f(x)图象上所有点向左平移个单位长度，得到y＝g(x)的图象，求y＝g(x)的图象离原点O最近的对称中心；‎ ‎(3)说明函数f(x)的图象是由y＝sin x的图象经过怎样的变换得到的．‎ ‎[解]　(1)根据表中已知数据，解得A＝5，ω＝2，φ＝－，数据补全如下表：‎ ωx＋φ ‎0‎ π ‎2π x Asin(ωx＋φ)‎ ‎0‎ ‎5‎ ‎0‎ ‎－5‎ ‎0‎ 则函数解析式为f(x)＝5sin.‎ ‎ ‎ ‎(3)把y＝sin x的图象上所有的点向右平移个单位长度，得到y＝sin的图象，再把y＝sin的图象上的点的横坐标缩短到原来的倍(纵坐标不变)，得到y＝sin的图象，最后把y＝sin 上所有点的纵坐标伸长到原来的5倍(横坐标不变)，即可得到y＝5sin2x－的图象．‎ ‎1.(2017·石家庄模拟)函数f(x)＝Asin(ωx＋φ)A>0，ω>0，|φ|<的部分图象如图所示，则f的值为(　　)‎ A．－ B．－ C．－ D．－1‎ ‎2.已知函数f(x)＝Acos(ωx＋φ)的图象如图所示，f＝－，则f＝(　　)‎ A．－ B．－ C. D. ‎[解析]‎ 由题图知＝－＝，‎ ‎∴T＝，即ω＝3，‎ 当x＝时，y＝0，即3×＋φ＝2kπ－，k∈Z，‎ ‎∴φ＝2kπ－，k∈Z，取k＝1，则φ＝－，‎ ‎∴f(x)＝Acos.‎ 则Acos＝－，解得A＝，‎ ‎∴f(x)＝cos，‎ 故f＝cos＝－.‎ ‎3.已知函数f(x)＝Asin(ωx＋φ)x∈R，ω、A>0,0<φ<的最大值为2，最小正周期为π，直线x＝是其图象的一条对称轴．‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)求函数g(x)＝f－f的单调递增区间．‎ ‎ ‎ ‎(2)g(x)＝2sin－2sin2＋ ‎＝2sin 2x－2sin ‎＝2sin 2x－2 ‎＝sin 2x－cos 2x ‎＝2sin.‎ 令2kπ－≤2x－≤2kπ＋，k∈Z，‎ 得kπ－≤x≤kπ＋，k∈Z.‎ 所以函数g(x)的单调递增区间是，k∈Z.‎ ‎1. (2017·西安模拟)函数y＝sin在区间上的简图是(　　)‎ 解析：选A　令x＝0，得y＝sin＝－，排除B、D.当x∈时，－≤2x－≤－，在此区间上函数不会出现最高点，排除C，故选A.‎ ‎2. (2016·四川高考)为了得到函数y＝sin2x－的图象，只需把函数y＝sin 2x的图象上所有的点(　　)‎ A．向左平行移动个单位长度 B．向右平行移动个单位长度 C．向左平行移动个单位长度 D．向右平行移动个单位长度 解析：选D　∵y＝sin＝sin，‎ ‎∴将函数y＝sin 2x的图象向右平行移动个单位长度，可得y＝sin的图象．‎ ‎3.函数f(x)＝2sin(ωx＋φ)ω>0，－<φ<的部分图象如图所示，则ω，φ的值分别是(　　)‎ A．2，－ B．2，－ C．4，－ D．4， 解析：选A　由图可得，＝－＝，∴T＝π，则ω＝2，∵图象过点B，∴2sin＝2，∴2×＋φ＝＋2kπ(k∈Z)，∵－<φ<，∴φ＝－.‎ ‎4. (2016·银川二模)已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0,0<φ<π)的图象与x轴的一个交点到其相邻的一条对称轴的距离为，若f＝，则函数f(x)在上的最小值为(　　)‎ A. B．－ C．－ D．－ ‎5. (2017·江西百校联盟联考)已知函数f(x)＝sin(ωx＋φ)的图象在y轴右侧的第一个最高点为P，在原点右侧与x轴的第一个交点为Q，则f的值为(　　)‎ A．1 B. C. D. 解析：选C　由题意得＝－，所以T＝π，所以ω＝2，则f(x)＝sin(2x＋φ)，将点P代入f(x)＝sin(2x＋φ)，得sin＝1，所以φ＝＋2kπ(k∈Z)．又|φ|<，所以φ＝，即f(x)＝sin(x∈R)，所以f＝sin＝sin＝，选C.‎ ‎6.已知函数f (x)＝sin(ωx＋φ)ω>0，－≤φ<的图象关于直线x＝对称，且图象上相邻两个最高点的距离为π.‎ ‎(1)求ω和φ的值；‎ ‎(2)当x∈时，求函数y＝f(x)的最大值和最小值．‎ 解：(1)因为f(x)的图象上相邻两个最高点的距离为π，‎ 所以f(x)的最小正周期T＝π，从而ω＝＝2.‎ 又因为f(x)的图象关于直线x＝对称，‎ 所以2×＋φ＝kπ＋，k∈Z，即φ＝kπ－，k∈Z，‎ 又－≤φ<，所以φ＝－.‎ 综上，ω＝2，φ＝－.‎ ‎(2)由(1)知f(x)＝sin，‎ 当x∈时，－≤2x－≤，‎ 所以，当2x－＝，即x＝时，f(x)最大值＝；‎ 当2x－＝－，即x＝0时，f(x)最小值＝－.‎ ‎____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎