吉林省吉林市2020届高三上学期第一次调研测试 数学（文）

吉林省吉林市2020届高三上学期第一次调研测试 数学（文）

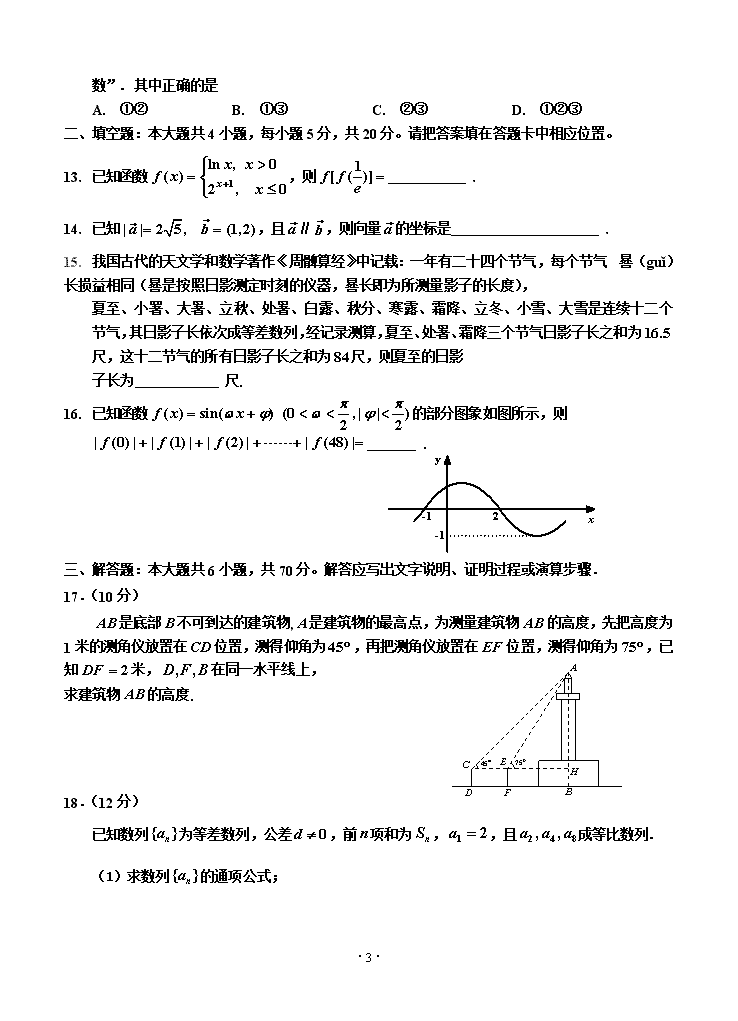
吉林市普通中学2019—2020学年度高中毕业班第一次调研测试 文科数学 本试卷共22小题，共150分，共4页，考试时间120分钟。考试结束后，将答题卡和试题卷一并交回。‎ 注意事项：‎ ‎1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条 形码、姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。‎ ‎2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案 的标号；非选择题答案必须使用‎0.5毫米黑色字迹的签字笔书写，字体工整、‎ 笔迹清楚。‎ ‎3．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案 ‎ 无效。‎ ‎4. 作图可先用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮 ‎ 纸刀。‎ 一、选择题：本大题共12题，每小题5分，共60分。在每小题给出的四个选项中，只有一个是符合题目要求。‎ ‎1. 已知集合，则 ‎ ‎ A. B. C. D. ‎ ‎2. 函数的最小正周期是 ‎ ‎ A. B. C. D. ‎ ‎3. 已知是△边上的中点，则向量 ‎ ‎ A． B． ‎ ‎ C． D． ‎ ‎4. 已知函数是奇函数，当时，；则当时，等于 ‎ A. B. ‎ C. D. ‎ ‎5. 已知正项等比数列满足，与的等差中项为，则的值为 ‎ ‎ A. B. C. D. ‎ ‎·8·‎ ‎6. 若，则 ‎ ‎ A． B． C． D． ‎ ‎7. 已知向量的夹角为，，则 ‎ ‎ A. B. C. D. ‎ ‎8. 将函数图象上的每个点的横坐标缩短到原来的一半，纵坐标不变; 再将所得图象向左平移个单位得到函数的图象，在图象的所有对称轴中，离原点最近的对称轴方程为 ‎ ‎ A. B. C. D. ‎ ‎9. 若函数且在上为减函数，则函数的图象 ‎ 可以是 ‎ ‎ A. B. C. D. ‎ ‎10. 在中， 、分别为、中点，‎ 则 ‎ ‎ A. B. C. D. ‎ ‎11. 等比数列的前项和为，若，‎ ‎ ，则 ‎ ‎ A. B. C. D. ‎ ‎12. 设函数的定义域为，若满足条件：存在，使在上的 ‎ 值域为（且），则称为“倍函数”，给出下列结论：‎ ①是“1倍函数”；②是“2倍函数”；③ 是“3倍函 ‎·8·‎ 数”. 其中正确的是 ‎ ‎ A. ①② B. ①③ C. ②③ D. ①②③‎ 二、填空题：本大题共4小题，每小题5分，共20分。请把答案填在答题卡中相应位置。‎ ‎13. 已知函数，则 .‎ ‎14. 已知，且∥，则向量的坐标是 .‎ ‎15. 我国古代的天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气 晷（guǐ）长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度），‎ 夏至、小署、大暑、立秋、处暑、白露、秋分、寒露、霜降、立冬、小雪、大雪是连续十二个节气，其日影子长依次成等差数列，经记录测算，夏至、处暑、霜降三个节气日影子长之和为尺，这十二节气的所有日影子长之和为尺，则夏至的日影 子长为 尺. ‎ ‎16. 已知函数的部分图象如图所示，则 ‎ .‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分） ‎ 是底部不可到达的建筑物,是建筑物的最高点，为测量建筑物的高度，先把高度为1米的测角仪放置在位置，测得仰角为，再把测角仪放置在位置，测得仰角为，已知米，在同一水平线上，‎ 求建筑物的高度. ‎ ‎18．（12分）‎ 已知数列为等差数列，公差，前项和为，，且成等比数列.‎ ‎（1）求数列的通项公式；‎ ‎·8·‎ ‎（2）设，记数列的前项和为，求证：.‎ ‎19.（12分）‎ 在中，角的对边分别是, 已知.‎ ‎（1）求角的值；‎ ‎（2）若，求的面积.‎ ‎20．（12分）‎ ‎ 设函数的正零点从小到大依次为，构成数列.‎ ‎ （1）写出数列的通项公式，并求出数列的前项和；‎ ‎ （2）设，求的值. ‎ ‎21．（12分）‎ ‎ 已知函数.‎ ‎（1）求函数的单调区间；‎ ‎（2）当时，求函数的最大值与最小值.‎ ‎22．（12分）‎ 已知函数.‎ ‎（1）当时，求函数在点处的切线方程；‎ ‎ （2）当时，恒成立，求实数的最大值.‎ ‎·8·‎ 吉林市普通中学2019—2020学年度高中毕业班第一次调研测试 文科数学参考答案与评分标准 一、选择题：‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B B A D A C A D D C B D 二、填空题：‎ ‎13. 1‎ ‎14. ‎ ‎15. 1.5（注：填也正确）‎ ‎16. ‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分） ‎ 解：中，‎ ‎ （米） --------------------------------5分 ‎ ‎ ‎ 因为 ‎ ‎ ‎ 所以（米）‎ ‎ 所以建筑物的高度为（）米 ---------------------------------------------10分 注：直接用不扣分 ‎18．（12分）‎ ‎·8·‎ 解（1）由题意得：，‎ ‎ 整理得， 因为，所以， --------------------------5分 ‎ 所以 ----------------------------------------6分 ‎（2） ---------------------------9分 ‎ ‎ ‎ 即 ------------------------------------------------12分 ‎19.（12分）‎ 解：（1）由正弦定理可得， -------------------2分 ‎ ‎ ‎ ---------------------------------------------------------5分 ‎ ，, -------------------------6分 ‎（2）‎ ‎ -----------------------------------------------10分 ‎ --------------------------------------------12分 ‎20．（12分）‎ 解：（1） -----------------------------------------------------3分 ‎ ‎ ‎ ‎ ‎ -----------------------------------------------------------------------6分 ‎（2） ------------------------------------------------------------8分 当时，‎ ‎ -------------10分 ‎·8·‎ ‎ 当时，‎ ‎ ------12分 ‎21．（12分）‎ 解：（1） ----------------------3分 ‎ 当时，，单调递增；‎ ‎ 当时，，单调递减；‎ ‎ 当时，，单调递增；---------------------------------------5分 ‎ 所以的递增区间是、；递减区间是 -----------------6分 ‎（2）由（1）知，在区间上单调递增，在区间上单调递减 ‎ 所以 -----------------------------------8分 ‎ 又因为 ----------------------------------------------------------10分 ‎ 所以的最大值是，最小值是 --------------------------------------------12分 ‎22．（12分）‎ 解：（1）， ----------------------------------------------2分 ‎ ‎ ‎ 所以切线方程为，即 -------------------------------------4分 ‎（2）‎ 当时，，不等式恒成立，； ---------------------------------------5分 当时，，所以 ‎ 设， ------------------------9分 ‎ 时，，为减函数 ‎ 时，，为增函数 ----------------------------------11分 ‎ 所以，‎ ‎ 综上：， 所以的最大值是. ------------------------------------------12分 ‎·8·‎ ‎（2）另解：‎ ‎ ‎ ‎ 当时，因为，所以不等式恒成立 --------------------------------------6分 ‎ 当时， ----------8分 ‎ ，，在区间上单调递减 ‎ ，不等式成立 ------------------------------9分 ‎ ， 时， ，单调递增 ‎ 时，，单调递减 --------------------11分 ‎ 所以 ‎ 由题意，解得 ‎ ‎ 综上：， 所以的最大值是. ----------------------------------------------12分 ‎·8·‎