- 2021-06-19 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广西桂林市、崇左市、防城港市2013届高三第二次联合模拟考试数学理
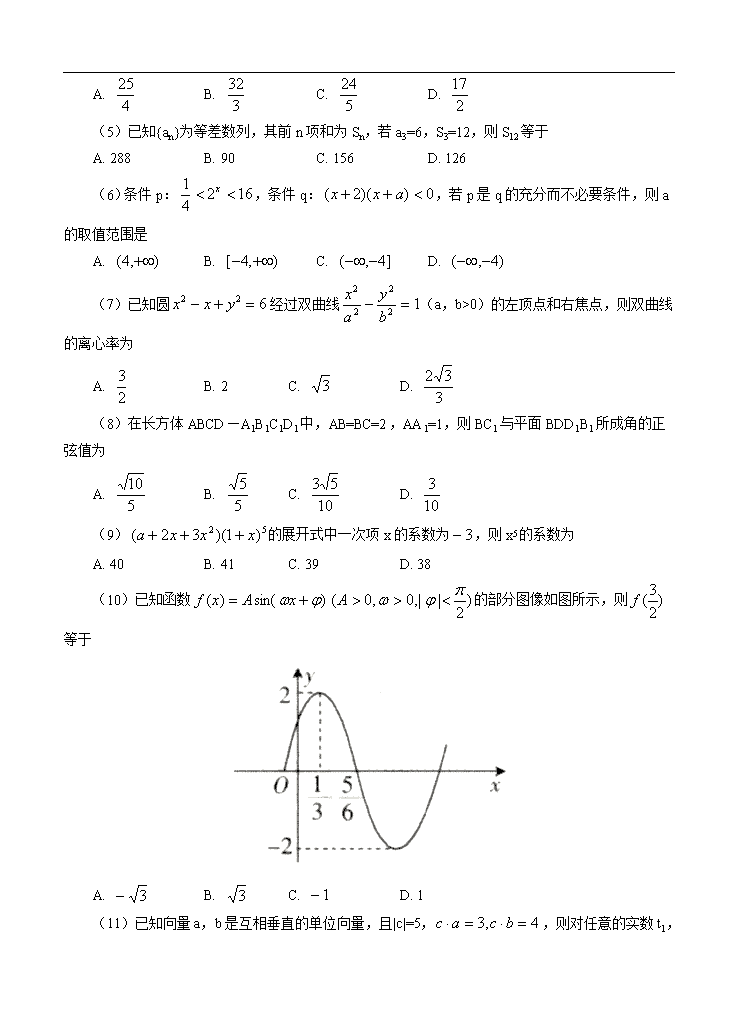
桂林市 崇左市 防城港市2012-2013学年下学期高三年级第二次联合模拟考试 数学试卷(理科) 第Ⅰ卷 注意事项: 第Ⅰ卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 参考公式: 如果事件A、B互斥,那么 球的表面积公式 P(A+B)=P(A)+P(B) 如果事件A、B相互独立,那么 其中R表示球的半径 球的体积公式 如果事件A在一次试验中发生的概率是p,那么 n次独立重复试验中事件A恰好发生k次的概率 其中R表示球的半径 一、选择题。(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。) (1)已知全集,集合, ,则集合U()等于 A. {1,2,5} B. {3,4} C. {3,4,5} D. {1,2} (2)复数z满足为虚数单位,则z等于 A. B. C. D. (3)已知,,则函数的反函数为 A. B. C. D. (4)已知椭圆,其左顶点为A,上顶点为B,右准线为l,则直线AB与直线l的交点的纵坐标为 A. B. C. D. (5)已知{an}为等差数列,其前n项和为Sn,若a3=6,S3=12,则S12等于 A. 288 B. 90 C. 156 D. 126 (6)条件p:,条件q:,若p是q的充分而不必要条件,则a的取值范围是 A. B. C. D. (7)已知圆经过双曲线(a,b>0)的左顶点和右焦点,则双曲线的离心率为 A. B. 2 C. D. (8)在长方体ABCD—A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BDD1B1所成角的正弦值为 A. B. C. D. (9)的展开式中一次项x的系数为,则x5的系数为 A. 40 B. 41 C. 39 D. 38 (10)已知函数的部分图像如图所示,则等于 A. B. C. D. 1 (11)已知向量a,b是互相垂直的单位向量,且|c|=5,,则对任意的实数t1 ,t2,取最小值时,的值为 A. 5 B. 7 C. 12 D. 13 (12)已知是以2为周期的偶函数,当时,,那么在区间内,关于x的方程有4个根,则k的取值范围为 A. 或 B. C. 或 D. 第Ⅱ卷 第Ⅱ卷共10小题,共90分。 二、填空题。(本大题共4小题,每小题5分,共20分。) (13)已知,cos,则=___________________。 (14)设x,y满足约束条件,则的最大值是____________。 (15)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,现要求甲安排在另外两位前面且丙不安排在周五,则不同的安排方法共有_______________种。 (16)已知底面为正三角形,侧棱长都相等的三棱锥S—ABC各顶点都在半球面上,其中A、B、C三顶点在底面圆周上,若三棱锥S—ABC的体积为,则该半球的体积为______________。 三、解答题。(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。) (17)(本小题满分10分) 在△ABC中,角A、B、C所对边分别是a、b、c,且。 (Ⅰ)求的值; (Ⅱ)若,求△ABC的面积。 (18)(本小题满分12分) 已知公比为q的等比数列{an}的前6项和为S6=21,且成等差数列。 (Ⅰ)求an; (Ⅱ)设{bn}是首项为2,公差为的等差数列,其前n项和为Tn,求不等式的解集。 (19)(本小题满分12分) 甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分。若甲、乙两名同学射击的命中率分别为和p,且甲、乙两人各射击一次所得分数之和为2的概率为,假设甲、乙两人射击互不影响。 (Ⅰ)若乙射击两次,求其得分为2的概率; (Ⅱ)记甲、乙两人各射击一次所得分数之和为,求的分布列和数学期望。 (20)(本小题满分12分) 如图,已知长方体ABCD—A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4,P为CC1的中点。 (Ⅰ)求证:BD⊥A1P; (Ⅱ)求二面角C—PD—B的大小。 (21)(本小题满分12分) 已知抛物线的焦点F与椭圆的一个焦点重合,直线l过点A(4,0)且与抛物线交于P、Q两点。 (Ⅰ)求p的值; (Ⅱ)若,试求动点R的轨迹方程。 (22)(本小题满分12分) 已知函数,其中a为大于零的常数。 (Ⅰ)若函数在区间内单调递增,求实数a的取值范围; (Ⅱ)求证:对于任意的,且n>1时,都有恒成立。 【试题答案】 题号 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) 答案 B A D B C D A A C A B B (13) (14)7 (15)14 (16) (17)解:(Ⅰ) ……2分 ……4分 (Ⅱ)由余弦定理得: , ……6分 又b+c=4,所以,即,由,得 ……8分 所以 ……10分 (18)解:(Ⅰ)∵、、成等差数列, ∴即,∴q=2 ……2分 则 ……3分 解得 ……4分 ∴ ……5分 (Ⅱ)由(Ⅰ)得,∴ ……7分 ……8分 ∴ ……10分 解得 即不等式的解集为 ……12分 (19)解:(Ⅰ)设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B,“甲射击一次,未击中目标”为事件,“乙射击一次,未击中目标”为事件, ……2分 则,,, ……3分 依题意得,解得 ……5分 所以乙射击两次得分为2的概率是 ……6分 (Ⅱ)的取值分别为0,2,4 ……7分 ……8分 ……9分 ∴的分布列为 0 2 4 P ……10分 ……12分 (20)解:(Ⅰ)连结A1C1,AC, ∵ABCD—A1B1C1D1是长方体, ∴A1A⊥面ABCD ……1分 又BD面ABCD,∴BD⊥A1A,又ABCD是正方形 ……2分 ∴BD⊥AC,AC∩A1A=A ∴BD⊥面A1AC,即BD⊥面A1ACC1 ……4分 又A1P面A1ACC1,∴BD⊥A1P ……6分 (Ⅱ)如图,以D为原点建立空间直角坐标系,由题意得 , 于是, ……8分 设面BDP, 不妨设,由得 ∴ ……10分 设面CDP,取, 若n1与n2的夹角为,则 ……11分 据分析,二面角C—PD—B是锐角,∴二面角C—PD—B的大小为 ……12分 (21)解:(Ⅰ)由椭圆的标准方程,得, ……1分 所以其焦点坐标为(±1,0), ……3分 又抛物线C的焦点与椭圆的一个焦点重合,所以,得p=2 ……5分 (Ⅱ)设, 由得, ……7分 所以 ……8分 而,可得……9分 又FR的中点坐标为M 当x1≠x2时,利用有,整理得 ……10分 当x1=x2时,R的坐标为(7,0),也满足 ……11分 所以即为动点R的轨迹方程 ……12分 (22)解:(Ⅰ) ……2分 由已知,得在上恒成立 即在上恒成立 ……4分 又∵当时,, ∴,即a的取值范围为 ……6分 (Ⅱ)由(Ⅰ)知函数在上为增函数, 当时,∵,∴ ……7分 即,对于,且n>1恒成立, ……9分 ……11分 ∴对于,且时,恒成立 ……12分查看更多